2. Syntax and Semantics

2.1. Brief introduction to the formal language theory

2.1.1. Definition of formal languages

alphabet

a set of characters

sentence

a sequence of characters

grammar

a set of rules to determine if a sentence is correct or not

language

a set of correct sentences

We often use tokens instead of alphabets because of simplicity. A token is something like a word composed of several letters.

An example of tokens

Sentence total = total + x; can be decomposed into a sequence of characters t, o, t, a, l, space, =, space, t, o, ..., which is cumbersome. Instead, we usually use a sequence of tokens total, =, total, +, x, ;.

Generative Grammar defines a language by generating correct sentences in some manner.

terminal symbols

Tokens used in languages

non-terminal symbols

Symbols representing structures of sentences. One of them is designated as the initial symbol.

production rules

Rules to rewrite some non-terminal symbols to other symbols.

Starting from the initial symbol, we can generate a correct sentence by repeatedly applying rules.

Simple grammar

  • Terminal: I, you, love

  • Non-terminal: S, N, V

  • Initial: S

  • Rule: S→NVN, N→I, N→you, V→love

There are several classes of grammars such as context-free grammar and regular grammar. Most of programming languages can be defined using context-free grammar.

2.1.2. BNF Notation

BNF (Backus-Naur Form) is a convenient notation to write a context-free grammar for practical use.

  • Terminal symbols are written as they are.

  • Non-terminal symbols are enclosed by < >.

  • Production rules are in the form non-terminal ::= symbols where we can write multiple alternatives by separating with | in the right side.

Simple arithmetic expression

Terminal: A, B, C, +, *, (, )

Non-terminal: <var>, <term>, <expr>

Initial: <expr>

Rule:

<var> ::= A | B | C
<term> ::= <var> | ( <expr> )
<expr> ::= <term> | <expr> + <term> | <expr> * <term>

2.1.3. Parse tree

To parse is to find how a sentence is generated by production rules. A parse tree is a tree structure that represents the result of parsing.

Generation of A*(B+C)

<expr> → <expr>*<term> → <term>*<term> → <var>*<term> → A*<term> → A*(<expr>) → A*(<expr>+<term>) → A*(<term>+<term>) → A*(<var>+<term>) → A*(B+<term>) → A*(B+<var>) → A*(B+C)

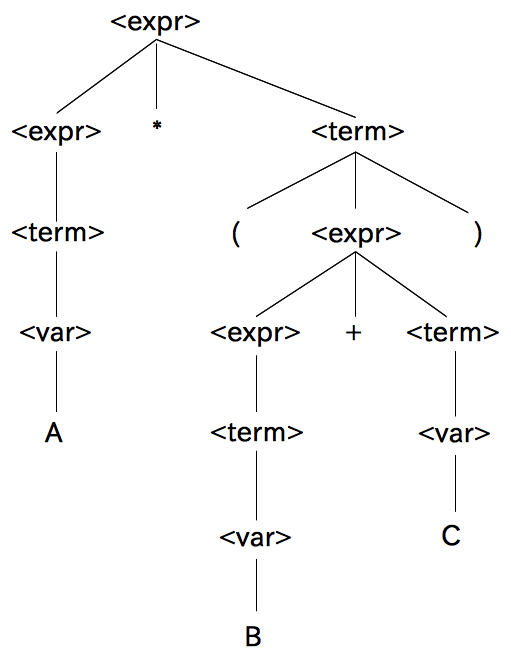
_images/parse-tree.png

Parse tree of A*(B+C)

Exercise 1

Draw a parse tree of A+B*C with the grammar shown above.

[Answer]

Exercise 2

In the grammar shown above, there is no precedence between + (add) and * (multiply). Change the grammar so that * (multiply) takes precedence over + (add). For example, when parsing A+B*C, make B*C be a subtree instead of A+B. Hint: introduce a new non-terminal symbol and a new rule so that + (add) and * (multiply) are parsed in separated levels.

[Answer]

2.1.4. Ambiguous grammar

We say a grammar is ambiguous if more than one parsing is possible for one sentence.

In a natural language

Structural ambiguity in English word-formation

An example of ambiguous grammar

We have two different parse trees for A*B+C with the following grammar.

<var> ::= A | B | C
<expr> ::= <var> | <expr> + <expr> | <expr> * <expr>

Dangling-else

Languages such as C and Java have the dangling-else problem since else is optional in if statements.

<if-statement> ::= if ( <expr> ) <statement> |
                   if ( <expr> ) <statement> else <statement>

Exercise 3

Explain the dangling-else problem in the following statement.

if ( x > 0) if ( y > 0 ) z = 1; else z = 2;

[answer]

Exercise 4

Explain that the following grammar is ambiguous.

<a> ::= <a> <a> | A

[answer]

2.2. Glance at the semantics theory

It is very difficult to define semantics of languages precisely. In C and Java, we usually say the meaning of ++ operator is “first evaluate the variable, then increment it”. However, we cannot figure out the result of x = 1; x = x++; with this definition. As long as we use a natural language, ambiguity is inevitable.

Semantics of languages are largely depend on their paradigms. Functional languages have lambda calculus, and logical languages have first-order predicate logic as the theoretical foundation of their semantics.

We have no obvious theoretical foundation for imperative (procedural) languages. However, there are several formal semantics theories that can give rigorous definition of semantics of imperative languages.

2.2.1. Operational semantics

The operational semantics describes how a program is executed as a sequence of computational steps.

  • A computational step is a change of state in the computer.

  • The state in the computer is, for example, a mapping from variables to values (a model of the memory device).

  • Using logical inference rules, we can define what kind of computational steps are possible.

2.2.2. Axiomatic semantics

The axiomatic semantics is based on Hoare logic. The meaning of a sentence is determined by a pair of precondition (which is true before the execution of the statement) and postcondition (which is true after the execution).

It is closely related to verification of a program. We can say a program is correct if it satisfies its specification. A specification is a pair of the initial condition and the final condition. Using Hoare Logic, we can prove a program satisfies its specification by chaining preconditions and postconditions of sentences.

2.2.3. Denotational semantics

The denotational semantics is based on recursive functions and domain theory.

It constructs mathematical objects that describe the meaning of a program. The interesting part is it includes an object that denotes an infinite loop.

Unfortunately, the constructed objects are often very hard to read (cf. Revised^5 Report on the Algorithmic Language Scheme).