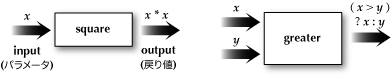
図10-1 squareとgreaterの機能図
Home >> Lecture 10
▼return文で値を返すときの書式終了する前に、このreturn文の後に続く式が評価されます。評価が終わって一定の値になりましたら、呼出し側にその値が戻されます。ここで返される値のことを戻り値(Return Value)あるいは返り値と呼んでいます。それでは、戻り値を返すようなメソッドを定義してみましょう。まず、戻り値を返すので、その型を記述します。今までは、戻り値がありませんでしたので、voidと記述してきました。たとえば、整数を返すのであれば、int と記述します。簡単なメソッドを定義してみましょう。
return <式> ;
int square( int x ) {
int y = x * x;
return y;
}
このsquareというメソッドは引数として受け取った値の2乗を計算して、計算結果を戻り値として返します。整数用になっていますので、仮引数も戻り値も型としてはint と記述されています。わかりやすくするために、ローカル変数yを用意して、それに計算結果を保持させるように記述しています。returnの後は、式を書くことができますので、このメソッドは直接的に次のように定義することもできます。
int square( int x ) {
return x * x;
}
もう1つの例を見てみましょう。2つの引数を受け取り、大きい方の数を返すメソッドを定義してみます。Lecture 7で出てきたif式を用いています。
int greater( int x, int y ) {
return ( x > y ) ? x : y;
}
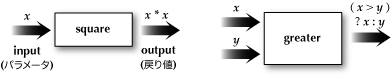
図10-1 squareとgreaterの機能図
▼戻り値のあるメソッドの呼出しもちろん、代入文など用意しないで、戻り値を受け取らなくても構いません。あるいは、メソッドの呼出しを複雑な式の中に埋没させても構いません。さて、それでは、先ほど定義したメソッドを、この書式に基づいて、呼び出して使うための記述をしてみましょう。変数を宣言しながら、代入を行なっています。
変数 = メソッド呼出し( 実引数 );
int z = square( 30 ); // zには900が代入される int y = square( z + 20 ); // yには846400が代入される int w = greater( z, y ); // wにも846400が代入される他の自作のメソッドと同様に、アプリケーション(クラス)自身のメソッドであることを示すためには、次のようにthisをつけて呼び出すこともできます。
int positive = this.square( -30 );このような呼出しを行なった場合、実際には、どのような実行の順番になっているのでしょうか?簡単な例を用いて、少し、実行の様子を追ってみましょう。 メソッドの呼出しの記述:
int result = square( 45 * 10 ); →45*10という式が評価されて、定数値450になり実引数としてsquareメソッドに渡されます。メソッドの定義:
int square( int x ) { return x * x ; }
→squareが呼び出され、仮引数変数xに、実引数の定数値450が代入されます。
→x * xと書かれた式の計算結果の定数値202500が戻り値として呼出し側に返送されます
メソッドの呼出し後の代入:
int result = square( 45 * 10 ); →square( 45 * 10 )の部分が、戻り値の定数値202500に置き替わります。 →変数resultを宣言し、result = 202500;という代入文が実行されます。このように、実行の制御が一度定義されたメソッドに移り、計算が行なわれた後、再び呼出し側に戻ってきました。呼出し側では、メソッドを呼び出した部分の記述が、戻り値に置き換えられます。
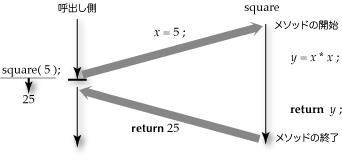
図10-2 squareメソッドの呼出しと戻り値の返送
printLine( "result:" + square( greater( 30, 40 ) - 10 ) ) );実際に、この1文がどのように実行されるかを追ってみましょう。
1. greater( 30, 40 )が実行される→評価結果は40になる
2. square( 40 - 10 )が実行される→評価結果は900になる
3. printLine( "result: " + 900 );が実行される
情報を返す: getColor, getFont, getName, getKey, getX, getY, getImage自分で定義する際にも、メソッドに名前をつけるときにこのような慣習を守っておくと、後でプログラムを読み返したときにわかりやすいでしょう。
論理値を返す: isVisible, isTurtle, isMouseDown, isKeyDown, equals
boolean isLunchTime( ) {
int hour = getHour( );
if ( hour >= 12 && hour < 14 ) {
return true ;
} else {
return false;
}
}
ところが、少し慣れてくると、論理型の変数に条件式が直接代入できることがわかります。 条件式は、trueかfalseに評価されますので、それを変数に代入して、その値を返してあげれば良いわけです。
boolean isLunchTime( ) {
int hour = getHour( );
boolean condition = ( hour >= 12 && hour < 14 );
return condition;
}
最後には、論理型の変数も使わずに、直接return文の戻り値を返す式のところに条件式を記述するようになります。
boolean isLunchTime( ) {
int hour = getHour( );
return hour >= 12 && hour < 14;
}
return文の戻り値の式は、条件式になっています。このように記述すると、条件式が評価されて、論理値のtrueあるいはfalseが返されることになります。今度は、このメソッドをstartメソッドなどの他のメソッドの中から呼び出して記述するような場合を考えてみましょう。
if ( isLunchTime( ) == true ) {
printLine( "It is lunch time! Shall we have lunch?" );
}
ところが、呼出し側でもこのように論理値と等しいかどうか比較しなくても、論理値そのものを返してくるのですから、if文の括弧の中に
メソッドの呼出しだけを直接記述することができます。比較結果は、どうせtrueかfalseという論理値に評価されることを
思い出して下さい。
if ( isLunchTime( ) ) {
printLine( "It is lunch time! Shall we have lunch?" );
}
このように論理値を戻り値として返すメソッドを用いる場合は、メソッドの呼出しを直接if文の条件式の中に記述して使います。
大きい方の数を返すメソッド、小さい方の数を返すメソッド、2つの値の平均値を返すメソッドを それぞれ作成し、ユーザの入力に応じて表示させるようにしなさい。クラス名はTwoIntegersValidaterとします。
整数を入力してもらうのに、タートル・グラフィックスのライブラリでは、 displayInputDialogとconvertToIntegerなどのメソッドを組み合わせて、 整数用、長整数用と実数用にダイアログを出して入力してもらい、入力値を返すメソッドを定義しています。 デフォルトの入力値を0とするようなものを新たに作ってみましょう。
int displayIntegerDialog( String s ) {
String answer = displayInputDialog( s, "0" );
return convertToInteger( answer );
}
long displayLongIntegerDialog( String s ) {
String answer = displayInputDialog( s, "0" ); // Javaの長整数表記のLが要らないことに注意
return convertToLongInteger( answer );
}
double displayNumberDialog( String s ) {
String answer = displayInputDialog( s, "0.0" );
return convertToNumber( answer );
}
この3つのメソッドをstartメソッドから呼び出して使ってみます。
public void start( ) {
int apples = displayIntegerDialog( "リンゴの個数を入力して下さい" );
long population = displayLongIntegerDialog( "地球の人口を入力して下さい" );
double radius = displayNumberDialog( "地球の赤道回りの円周を入力して下さい" );
}
カレンダー関係で必要なメソッドを記述してみましょう。 まず、引数に年を貰って閏年かどうかを論理値で返すメソッド(isLeapYear)です。 閏年ならtrueを、平年ならfalseを返します。
boolean isLeapYear( int year ) {
return year % 400 == 0 || year % 4 == 0 && year % 100 != 0 ;
}
次に、引数に年と月を貰って、その月の日数(整数)を返すメソッド(getMonthDays)です。 2月の場合は、isLeapYear( )を用いて閏年かどうかみています。 後は小の月の条件を論理式で記述しています。
int getMonthDays( int year, int month ) {
if ( month == 2 ) { if ( isLeapYear( year ) ) { return 29; } else { return 28; } }
else if ( month%2==0 && month<8 || month%2==1 && month>8 ) { return 30; }
else { return 31; }
}
次のメソッドは、上記のgetMonthDaysメソッドを用いて、 指定された年(year)において、指定された月(month)の最初の日が始まるまでの 日数を求めています。
int countDays( int year, int month ) {
int countday = 0;
for ( int m=1; m < month; m++ ) { countday += getMonthDays( year, m ); }
return countday;
}
2008年は閏年ですね。2月は29日で終わります。 それを踏まえて、ある年のある月とその月の日の3つの値を 入力してもらうと、その年の1月1日から数えて何日目であるかを求めることができます。 大の月と小の月、しかも2月は閏年かどうかも計算にいれなければいけません。 CountTotalDaysというクラス名で作成し、コンパイルし、実行します。
以下のメソッドは、1900年から、指定された年(year)の最初の日が始まるまでの日数を求めています。 グレゴリオ暦は、1582年〜1700年ぐらいまででヨーロッパで導入されましたが、 アジア圏で導入されたのは、1873年の日本からです。 1900年ぐらいまでは、ユリウス暦からのいろいろな調整で、日付が結構変更されていますので、 1900年から日数を数えることに致しました。 isLeapYearメソッドを用いて、閏年なら366を、平年なら365を足し込んでいっています。
int countAllDays( int year ) {
int countday = 0;
for ( int y=1900; y < year; y++ ) {
countday += ( isLeapYear( y ) ) ? 366 : 365;
}
return countday;
}
最後は、引数に年と月を貰って、その月の第1日目が何曜日で始まるかを整数で返すメソッドです。 指定された年(year)・月(month)の始まる前の日が1900年1月1日から数えて何日目であるか求めて、 その月の始まる曜日を求めています。 0…日曜日〜6…土曜日という形で求まります。 countAllDaysとcountDaysメソッドを用いています。
int getStartWeekDay( int year, int month ) {
int everyday = countAllDays( year ) + countDays( year, month );
return ( everyday + 1 ) % 7; // 1を足しているのは、1900年1月1日が月曜だから
}
1900年以降の年について、 入力された年、月、日について、その日の曜日を求めるようなプログラムを作成しなさい。 上記のgetStartWeekDayで入力された年と月が、1900年1月1日から、通算何日目であるかがわかります。 思考例として、2000年2000年1月1日から通算何日目を考えてみましょう。 たとえば、2003年の6月15日は、2000年が閏年なので366日、2001年と2002年が平年なので365日です。 2003年は平年なので、1月が31日、2月が28日、3月が31日、4月が30日、5月が31日あります。 そうすると、2003年6月15日は、2000年1月1日から数えて、366+365+365+31+28+31+30+31日と 加えて、6月の15日分になりますので、1262日目です。 2000年1月1日から数えていますので、何日経過したかといえば、-1して1261日経過しました。 これを1週間の7で割った余りを求めて下さい。1261%7→2になります。 それが曜日に対応する数値になります。 ちなみに2000年1月1日は、土曜日でしたから、この分も足さなければなりません。 日曜日=0,月曜日=1,火曜日=2,水曜日=3, 木曜日=4, 金曜日=5, 土曜日=6としています。 ですから、土曜日に対応する6を足します。(1+6)%7→0です。0は日曜日ということです。 CalculateWeekDayというクラス名で作成し、コンパイルし、実行します。 余裕のある人は指定された年の十二支も 表示するようにしてみなさい。ちなみに2000年は辰年でした。
上記のメソッドを利用して、指定された年・月のカレンダーを表示するプログラムを作りなさい。 クラス名は、DisplayCompleteCalendarにて。
タートル・グラフィックスでは、現在タートルがどちらを向いているかを getAngleメソッドで、 現在タートルの中心がどこにいるかの位置を getXメソッドと getYメソッドで 求めることができます。これらは実数で返してくれます。 getIntegerXメソッドと getIntegerYメソッドは、 整数で返してくれます。 これらのメソッドは戻り値がありますので、次のように変数に代入したりして値を得ます。
double angle = turtle.getAngle( ); double x = turtle.getX( ); double y = turtle.getY( ); int x = turtle.getIntegerX( ); int y = turtle.getIntegerY( );
これらのメソッドは、タートルの状態を知るために非常に有用です。 なお、タートルの方向はマイナスで表されることもあります。以下の図を参照にして、現在タートルが どちらを向いているのかを把握してプログラムしてください。
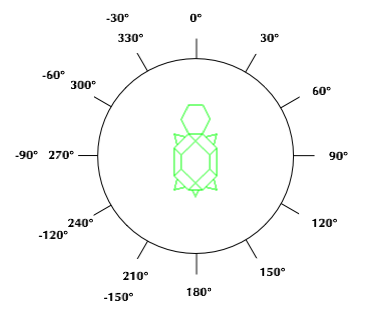
図10-3 タートルの方向
以下のプログラムでは、タートルが現在どちらを向いているかを、それぞれの頂点にきたときに、 getAngleメソッドで求めて、それを文字端末(ターミナル)に表示するものです。 このようなタイミングで必要な情報を文字端末に表示させることをデバッグプリント(Debug Print)と 呼びます。 デバッガでいちいちプログラムを止めるよりも、必要な時点での変数やタートルの状態がわかり、 それが表示として残こっていきます。 そのため、多くのプログラマはデバッガを使うときは、よほど根拠が掴めない特殊な場合だけに限る ようにしています。 熟練プログラマは、デバッガを殆ど使わずに、デバッグプリント、つまりプログラム上のある地点に おける変数の値の移り変わりをトレースするだけで問題点を掴み、プログラムを修正していきます。
import sfc.turtle.TurtleFrame;
import sfc.turtle.Turtle;
public class SeaUrchin extends TurtleFrame{
public static void main(String [ ] args) { new SeaUrchin( ); }
public void start( ) {
Turtle turtle = new Turtle( this );
turtle.rotate( 6 );
for ( int i=1; i <= 18 ; i++ ) {
turtle.forward( 30 );
printLine( i + "番目の外頂点での角度" + turtle.getAngle( ) );
turtle.rotate( 168 );
turtle.forward( 30 );
printLine( i + "番目の内頂点での角度" + turtle.getAngle( ) );
turtle.rotate( -168 + 360 / 18 );
}
}
}

上記の「うに」のような図形は、棘が18本でしたが、これをユーザが入力できるようにしてみなさい。 値としては、3〜60までの整数値の範囲で受け取るように入力をガードしなさい。 クラス名はSeaUrchinDrawerとします。
タートルは、次のような2つのメソッドで直接ウィンドウの特定の座標に置くことができます。
setLocation( x座標, y座標 )
moveTo( x座標, y座標 )
両者の違いは、setLocationがアニメーションを伴わないで、一瞬その位置に置かれるのに対して、 moveToは、タートルが目的地にまず回転して、それから歩いて移動するアニメーションを伴います。 ただし、ペンを上げていないと、初期の位置から、その座標まで軌跡が引かれることになります。 ウィンドウの座標は、左上の端がx座標0, y座標0で、x座標は右側にプラスになるのですが、 「y座標は下方向がプラスになる」という特性を持っています。 ほとんどのウィンドウのプログラミングができるライブラリにおいて、同じような座標系を 持っています。y座標の方向が違うことに注意して下さい。

次のプログラムは、配列の初期値を代入して、タートルを目的の座標に向かわせるものです。 x座標の配列とy座標の配列を持っています。ただし、x座標の配列の要素の値が -10ならばpendown、-20ならばpenupをさせるようにしています。 startメソッドの中だけを記述します。
public void start( ) {
int tx [ ] = { 100, -10, 300, 300, 220, 220, 180, 180, 100, 100, -20,
320, -10, 360, 360, 440, 480, 390, 480, 440, 360, 360, 320, 320 };
int ty [ ] = { 100, -10, 100, 140, 140, 300, 300, 140, 140, 100, -20,
100, -10, 100, 180, 100, 100, 200, 300, 300, 220, 300, 300, 100 };
Turtle turtle = new Turtle( this );
turtle.setPenColor( Blue );
turtle.penup( ); // 最初はペンを上げた状態にしておきます
turtle.moveTo( tx[ 0 ], ty[ 0 ] ); // 最初の位置に移動します。
for ( int i=1; i < tx.length ; i++ ) {
if ( tx[ i ] == -10 ) { turtle.pendown( ) ; } //-10だったら、ペンを下ろす
else if ( tx[ i ] == -20 ) { turtle.penup( ) ; } //-20だったら、ペンを上げる
else{ turtle.moveTo( tx[ i ], ty[ i ] ); } // それ以外は要素の示す座標へ移動する
}
}
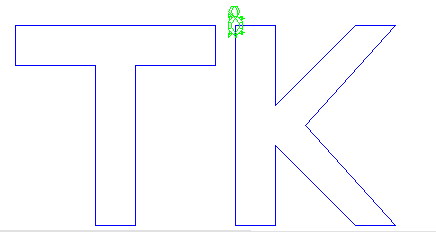
上記のプログラムは、下記の図のようにTKと描くようにしました。他にも直線的なアルファベット (AEFHILMNVWXYZ)を描くように配列の初期値を修正してみてください。 クラス名はPractice1004とします。
タートルグラフィックスでは、4角形や角の取れた4角形を描くのに非常に苦労します。そこで、 使い捨てのタートルを使って(軌跡を残すためだけにしか使われない)、矩形(4角形のこと)を描く 便利なメソッドを定義してみましょう。左上のx, y座標と、幅(width)と高さ(height)の4つの引数を 渡すようにします。 下記のメソッドの記述で、hideTurtle は、軌跡は残して、タートルだけは表示しないという機能を実行するメソッドです。
void drawRectangle( int x, int y, int width, int height ) {
Turtle turtle = new Turtle( this );
turtle.penup( );
turtle.setLocation( x, y );
turtle.pendown( );
int i=1;
while ( i <= 4 ) {
turtle.rotate( 90 );
if ( i % 2 == 1 ) { turtle.forward( width ) ; } // 奇数だったら幅分だけ移動
else{ turtle.forward( height ); } // 偶数だったら高さ分だけ移動
i = i + 1;
}
turtle.hideTurtle( );
}
これでは、黒の矩形しか描きませんので、java.awt.Colorクラスを使って、色の指定ができるように します。そうすると、上記のメソッドは次のように記述することができます。Javaでは同じ名前のメソッドでも、 引数の数が違えば、シグネチャが異なりますので、違うメソッドとして認識してくれます。
void drawRectangle( int x, int y, int width, int height, java.awt.Color c ) {
Turtle turtle = new Turtle( this );
turtle.penup( );
turtle.setLocation( x, y );
turtle.setPenColor( c );
turtle.pendown( );
int i=1;
while ( i <= 4 ) {
turtle.rotate( 90 );
if ( i % 2 == 1 ) { turtle.forward( width ) ; } // 奇数だったら幅分だけ移動
else{ turtle.forward( height ); } // 偶数だったら高さ分だけ移動
i = i + 1;
}
turtle.hideTurtle( );
}
これまでは枠だけでしたが、色が指定できるなら、塗りつぶしたくなるのが、人の心情ってぇものです。 塗りつぶすメソッドを記述してみましょう。
void fillRectangle( int x, int y, int width, int height, java.awt.Color c ) {
Turtle turtle = new Turtle( this );
turtle.penup( );
turtle.setLocation( x, y );
turtle.setPenColor( c );
turtle.rotate( 90 );
turtle.pendown( );
int i=1;
while ( i <= height ) { // 高さ分だけ繰返しを実行
turtle.forward( width ); // 横線で描画していきますので、幅分だけ移動
if ( i % 2 == 1 ) { turtle.rotate( 90 ); } // 奇数回は時計回り、偶数回は半時計回り
else{ turtle.rotate( - 90 ); }
if ( i < height ) {
turtle.forward( 1 ); // 1ドット下に降ります
if ( i % 2 == 1 ) { turtle.rotate( 90 ); } else{ turtle.rotate( - 90 ); }
}
i = i + 1;
}
turtle.hideTurtle( );
}
さて、次はボタンなどに使われるちょっと角の取れた矩形を描くようにします。角の丸みをどれくらいに するかを併せて指定するようにします。丸みを帯びた角は、10度ずつ9回、90度分の円弧を描くようにしています。
void drawRoundRectangle( int x, int y, int width, int height, int r, java.awt.Color c ) {
Turtle turtle = new Turtle( this );
turtle.penup( );
turtle.setLocation( x, y );
turtle.setPenColor( c );
turtle.rotate( 90 );
turtle.forward( r );
turtle.pendown( );
int i=1;
while ( i <= 4 ) {
if ( i % 2 == 1 ) { turtle.forward( width - 2 * r ); } // 左右の丸み分だけ移動距離は少なくなります
else { turtle.forward( height - 2 * r ); } // 上下の丸み分だけ移動距離は少なくなります
int j=1;
for ( j <= 9 ) { // 角の丸みを描いています
turtle.rotate( 10 );
turtle.forward( 0.5 * r * Math.PI / 9 );
j = j + 1;
}
i = i + 1;
}
turtle.hideTurtle( );
}
これらのメソッドをstartメソッドから呼び出して使ってみます。
public void start( ) {
drawRectangle( 10, 10, 80, 40 );
drawRectangle( 100, 10, 80, 40, Red );
fillRectangle( 190, 10, 80, 40, Magenta );
drawRoundRectangle( 280, 10, 80, 40, 6, Blue );
}

矩形を塗り潰すときは、同じ色で塗りつぶしましたが、これを、白から赤へのグラデーション (Colorオブジェクトを作るときに赤色成分だけを変化させる)で塗りつぶすようなメソッドを作ってみなさい。 1つの横線を描くたびに色を変えていきます。余裕がある人だけがやってください。 クラス名はGradationDrawerとします。
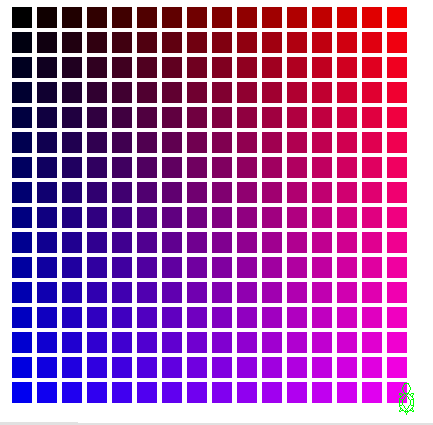
矩形(四角形)領域を軌跡で塗りつぶすプログラムを利用して、緑色は0で構いませんから、青色、赤色をそれぞれ、 0から240まで16ずつ変化させながら、格子を描くプログラムを記述して見なさい。格子を描く開始位置を指定するのには、 setLocation( ) メソッドを使っても良いでしょう。クラス名は、ColorTableとします。 以下の記述を参照しなさい。
turtle.setPenColor( new java.awt.Color( red, 0, blue ) ); // 軌跡の色をred, 0, blueの3原色で混色される色にする。
次は中心のx, y座標と半径、および色を指定して、円(正確には正60角形)を描画するメソッドを 定義してみましょう。
public void drawCircle( int x, int y, int r, java.awt.Color c ) {
Turtle turtle = new Turtle( this );
turtle.penup( );
turtle.setLocation( x, y ); // まず中心座標に行って
turtle.forward( r ); // 半径分だけ上に登ります
turtle.rotate( 90 ); // そこで右に向いて
turtle.setPenColor( c ); // ペンの色を設定して
turtle.pendown( ); // 描き始めです
int i=1;
while ( i <= 60 ) {
turtle.forward( 2 * Math.PI * r / 60 ); // 1回分の進む距離を求めています
turtle.rotate( 6 );
i = i + 1;
}
turtle.hideTurtle( );
}
円は、必ず中心を指定するだけはなく、矩形と同じように左上の座標を指定する場合があります。 正方形に内接する円(円弧がちょうど正方形の各辺のどこかに触れる円)は一意に指定できます。 このことを利用して、左上のx, y座標と直径、および色を指定して、円を描画するメソッドを定義して みましょう。半径が直径になった以外は、単に最初に行く場所の記述の式が違うだけです。はい。
public void drawCircleSquare( int x, int y, int size, java.awt.Color c ) {
Turtle turtle = new Turtle( this );
turtle.penup( );
turtle.setLocation( x+size/2, y+size/2 );
turtle.forward( size/2 );
turtle.rotate( 90 );
turtle.setPenColor( c );
turtle.pendown( );
int i=1;
for ( i <= 60 ) {
turtle.forward( Math.PI * size / 60 );
turtle.rotate( 6 );
i = i + 1;
}
turtle.hideTurtle( );
}
円を塗りつぶしてみましょう。これは、中心から、1ドットずつ移動して、同心円を描いていきます。 うまく塗りつぶせるでしょうか。
public void concentricCircle( int x, int y, int r, java.awt.Color c ) {
Turtle turtle = new Turtle( this );
turtle.penup( );
turtle.setLocation( x, y ); // まずは中心座標に行き
turtle.setPenColor( c );
turtle.pendown( );
int i=1;
while ( i <= r ) { // 1ドット登らせます
turtle.forward( 1 );
turtle.rotate( 90 );
int j=1;
while ( j <= 60 ) { // 円(同心円)を描かせます
turtle.forward( 2 * Math.PI * i / 60 ); // 1回に進む距離は中心からの離れぐらいで異なります
turtle.rotate( 6 );
j = j + 1;
}
turtle.rotate( -90 );
i = i + 1;
}
turtle.hideTurtle( );
}
塗りつぶしをするものがいま一つな感じがあります。やはり、三角関数と逆三角関数を用いて横の長さを計算して、 矩形のときのように横に線を引いて塗りつぶしていきましょうか。そうしたものが以下のメソッドになっています。
public void fillCircle( int x, int y, int r, java.awt.Color c ) {
Turtle turtle = new Turtle( this );
turtle.penup( );
turtle.setLocation( x, y ); // まずは中心座標に行き
turtle.forward( r ); // 半径分だけ縦に登らせます
turtle.setPenColor( c );
turtle.rotate( 90 );
int i=1;
while ( i <= 2 * r ) {
double size = Math.sin( Math.acos( (r-i) / (double)r ) ) * r ; // この式は横の長さを求めています
turtle.forward( size ); // 右側に移動しておき
turtle.rotate( 180 ); // くるりときびすを返します
turtle.pendown( );
turtle.forward( size * 2); // この左側への移動で横線を描画します
turtle.penup( );
turtle.rotate( 180 );
turtle.forward( size ); // 左端から、また真ん中に戻ってきます
turtle.rotate( 90 );
turtle.forward( 1 ); // 1ドット分下に降ります
turtle.rotate( -90 );
i = i + 1;
}
turtle.hideTurtle( );
}
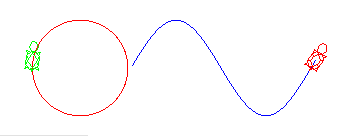
上記の4つの円を描くメソッドをstartメソッドから呼び出して使ってみます。
public void start( ) {
drawCircle( 60, 60, 40, Red );
drawCircleSquare( 120, 20, 80, Magenta );
concentricCircle( 260, 60, 40, Orange );
fillCircle( 360, 60, 40, Blue );
}

円を塗り潰すときは、同じ色で塗りつぶしましたが、これも、中心が白で外側に行くに従って赤へ変化するグラデーション (Colorオブジェクトを作るときに赤色成分だけを変化させる)で塗りつぶすようなメソッドを作ってみなさい。 1つの同心円を描くたびに、色を変えながら描画していきます。余裕がある人だけがやってください。 クラス名はGradationCircleとします。
int width = getWidth( ); // ウィンドウの幅を得る setWidth( width * 2 ); // 現在の幅の2倍の幅にする setHeight( 400 ); // ウィンドウの高さを400に固定する
setBackgroundColor( Red ); // 赤に設定する setBackgroundColor( new java.awt.Color( 244, 20, 128 ) ); // 3原色を指定して
setWaitTurtle( false ); // タートルを待たないようにする fillRectangle( 10, 100, 200, 40 ); // Lecture 8で作った矩形塗りつぶしメソッドを呼ぶ setWaitTurtle( true ); // この後は通常の速度で
import sfc.turtle.TurtleFrame;
import sfc.turtle.Turtle;
public class SkyAndGround extends TurtleFrame {
public static void main(String [ ] args) { new SkyAndGround( ); }
public void start( ) {
setWidth( 800 );
setHeight( 400 );
setWaitTurtle( false );
setBackgroundColor( new java.awt.Color( 200, 128, 80 ) );
Turtle turtle = new Turtle( this );
int halfheight = getHeight( ) / 2;
turtle.penup( );
turtle.setLocation( 0, halfheight );
turtle.rotate( 90 );
turtle.pendown( );
for ( int i=0; i <= halfheight ; i++ ) {
turtle.setPenColor( new java.awt.Color( 0, 255-(255*i/halfheight), 255 ) );
turtle.forward( getWidth( ) );
turtle.rotate( (i % 2 == 0) ? -90 : 90 );
turtle.forward( 1 );
turtle.rotate( (i % 2 == 0) ? -90 : 90 );
}
turtle.hideTurtle( );
}
}

▼オブジェクト配列の宣言の書式同じように配列の領域を確保するのは次のように記述します。
クラス名 配列名 [ ]; あるいは
クラス名 [ ] 配列名;
▼データ領域を確保する書式配列のサイズとは、データをいれる要素の個数を示します。整数式で記述します。たとえば、先ほどの2つの配列変数aとbにそれぞれデータ領域を確保してみましょう。
配列名 = new クラス名[ サイズ ];
a = new String[ 10 ]; // 配列 aに、10個のStringのデータ領域を確保する b = new Color[ 5 ]; // 配列 bに、5個のColorのデータ領域を確保するもちろん、通常の変数と同様に、データ領域を確保しながら宣言することもできます。
▼宣言と共にデータ領域を確保する書式たとえば、次の2つの配列は、それぞれカラーとボタン用の配列となります。
型名 配列名 [ ] = new 型名[ サイズ ]; あるいは
型名 [ ] 配列名 = new 型名[ サイズ ];
Color colors [ ] = new Color[ 20 ]; // 20個のカラーオブジェクト用の配列 Turtle turtles [ ] = new Turtle[ 10 ]; // 10個のタートルオブジェクト用の配列後は、通常の配列のように用いることができます。配列の要素を指定する場合は、通常のオブジェクトを参照している変数のように用いることができます。
colors[ 3 ] = new Color( 10, 30, 40 ); // 3番目の要素にカラーオブジェクトを生成
for ( int i = 0; i < turtles.length; i++ ) { // 配列のすべてのタートルに対して
turtles[ i ] = new Turtle( this); // 個々の要素にタートルオブジェクトを生成
turtles[ i ].penup( );
turtles[ i ].setLocation( 20, i*40+20 ) // アプレットの画面上に配置
}
turtles[ 3 ].setTurtleColor( colors[ 3 ] ); // 3番目のタートルのカラーを変える
上の例をみてもわかるように、オブジェクトの配列は、オブジェクトそのものを生成したのではありません。new文では配列を1つ生成にしただけに過ぎません。ですから、配列の要素となる個々のオブジェクトは、その都度繰返しなどを使ってnew文を使ってそれぞれを生成していく必要があります。これが、通常の整数などの配列と異なる点です。
| <<Previous Lecture | >>Next Lecture |