Home >> Columns >> Algorithms on Integer
(64, 28)→(28, 8)→(8, 4)→4が最大公約数最大公約数を求めるやり方です。古代ギリシャのユークリッドが考えました。2つの正の整数の最大公約数は、大きい方の数から小さい方の数で割りきれればその小さい方の数が最大公約数であるというものです。割りきれなければ、2つの数の差と小さい方の数で同じ事を繰り返します。
int gcd( int a, int b ) {
while ( true ) {
if ( a > b ) {
if ( a % b == 0 ) { return b; } else { a = a - b; }
} else {
if ( b % a == 0 ) { return a; } else { b = b - a; }
}
}
}
あるいは、2つの数の差を取る替わりに、大きい数と小さい数の余りを取るというやり方もあります。この方が早く解に辿り着けます。再帰を使って記述してみました。
int gcd( int a, int b ) {
if ( a > b ) { return ( a%b == 0 ) ? b : gcd( b, a % b ); }
else { return (b%a == 0 ) ? a : gcd( a, b % a ); }
}
2つの整数をコンソールから入力してもらい、最大公約数を求めて表示するプログラムを作成しなさい。 クラス名は、GreatestCommonDiviserとします。引き算で行なう方法と、剰余で行なう方法について、 途中で求まる2つの数をコンソールに表示して、どのように収束して求まっていくのかの過程についても 表示するようにしなさい。
最小公倍数を求めるプログラムを、最大公約数を求めるメソッドを利用して作りなさい。
3の二乗+4の二乗=5の二乗でした。このような関係にある3つの数を、 1〜100までの間で求めなさい。
x: 0 1 2 3 4 5 6 7 8 9
x2: 0 1 4 9 16 25 36 49 64 81
\/ \/ \/ \/ \/ \/ \/ \/ \/
第1階差: 1 3 5 7 9 11 13 15 17
\/ \/ \/ \/ \/ \/ \/ \/
第2階差: 2 2 2 2 2 2 2 2
これを利用し、任意のpx2 + qx + rという二次方程式について、掛け算を使わないで、計算するプログラムを作りなさい。整数で行ないなさい。pとq、およびrには、適当な整数の定数を代入しておきます。xを1から10ぐらいまで変化させ、そのときに、その二次方程式に適用したときの計算結果を出すようにfor文で作ります。もちろん、第1階差の初項と第2階差を求めるとき以外は、掛け算を使わないで、足し算だけで求めていきます。クラス名は、Differentialにします。なお、チャールズ・バベッジは、階差機関を発展させていろいろな方程式を求めることができる解析機関を歯車で試作しようとしました。これは、現在のコンピュータの元祖の一つになっています。
ヒント:px2 + qx + rの第1階差は、p*(2 *x+1)+q(すなわちp*(x+x+1)+q)になります。第2階差は、2p(すなわちp+p)になります。x=0のときの、最初の計算結果、第1階差、第2階差を求めておき、それを求められる数にxが達するまで足し合わせていきます。すなわち以下のように計算結果には、第1階差を足し込みますし、第1階差には第2階差を足し込みます。ここで、Javaの自己参照代入分から1つ前と新しい値は、1つの変数で表わせることを思い出しましょう。
答え = 1つ前の答え + 第1階差
第1階差 = 1つ前の第1階差 + 第2階差
中心のx, y座標を指定して、円の半径を指定して、その円に外接(頂点が演習のどこかに接する)、正n角形を 描画するようなメソッドdrawPolygon( int x, int y, int radius, int n )を定義して、startメソッドから呼び出して 使ってみなさい。

今月のカレンダーをダイアログに表示するプログラムを作成しなさい。 タートル・グラフィックスのgetYear( )、getMonth( )などを利用しなさい。 DisplayCalendarとします。まずは、簡単にその月が日曜日始まりで、31日あるものとして始めます。 その月が何日あるかは、小の月、大の月の条件を考えて下さい。2月は閏年のことも考えてください。 その月が何曜日から始まるかは、getDay( )とgetWeekDay( )から計算します。たとえば、getDay( )が4で、 getWeekDay( )が6だったら、その月の1日は水曜日始まりだというのがわかります。 その月の始まる曜日は、(今日の曜日+7 -(今日の日-1)%7 ) % 7 で求められます。
int linearSearch( int target , int a[ ] ) {
for ( int i=0; i < a.length; i++ ) {
if ( a[ i ] == target ) { return i; }
}
return -1;
}
int binarySearch( int target, int a[ ] ) {
int least = 0, most = a.length;
while ( least <= most ) {
int middle = (least+most) / 2;
if ( a[ middle ] > target ) { most = middle + 1; }
else if ( a[ middle ] < target ) { ieast= middle -1; }
else { return middle; }
}
return -1;
}
2分検索法を使えば、配列の要素がn個あったとしても、1回の比較で件数を半分にしていきますので比較回数は、log2 n回で終わります。要素の個数が膨大になっても、比較回数は非常に少なくてすみます。
ArrayListを使って2分検索法を実現するメソッドを作成し、利用して見なさい。
void straightSelection( int a[ ] ) {
int min;
for ( int i = 0; i < a.length-1; i++ ) {
min = i;
for ( int j=i+1; j < a.length; j++ ) { // 一番小さいものを探す
if ( a[ min ] > a[ j ] ) { min = j; }
}
int temp = a[ min ]; a[ min ] = a[ i ]; a[ i ] = temp; // 現在の先頭の要素と交換する
}
}
直接選択法による並べ替えの例として、int a[ ] = { 19, 64, 3, 30, 10, 39, 20, 53 };という初期値が代入されている配列を考えます。図において、↑が変数が指している要素を示します。枠が現在対象となっている範囲です。
直接選択法のソーティングの様子:
19 64 3 30 10 39 20 53
↑i ↑min
3 64 19 30 10 39 20 53
↑i ↑min
3 10 19 30 64 39 20 53
↑i, min
3 10 19 30 64 39 20 53
↑i ↑min
3 10 19 20 64 39 30 53
↑i ↑min
3 10 19 20 30 39 64 53
↑i, min
3 10 19 20 30 39 64 53
↑i ↑min
void bubbleSort( int a[ ] ) {
for ( int i=1; ifor ( int j=a.length-1; j >= i ; j-- ) {
if ( a[ j-1 ] > a[ j ] ) { int temp = a[ j -1 ]; a[ j - 1 ] = a[ j ]; a[ j ] = temp; }
}
}
}
先ほどと同じ配列を使って直接選択法による並べ替えの例を見てみます。図において、←が交換されて前に移動することを示しています。枠が現在対象となっている範囲です。
直接交換法のソーティングの様子
19←64←3 30←10 39←20 53
3 19←64←10 30←20 39 53
3 10 19 64←20 30 39 53
3 10 19 20 64←30 39 53
3 10 19 20 30 64←39 53
3 10 19 20 30 39 64←53
3 10 19 20 30 39 53 64
void straightInsertionSort( int [ ] a) {
for ( int i=1; i < a.length; i++) {
int j, target = a[ i ];
for ( j=i -1; j >= 0 && a[ j ]>target ; j-- ) { a[ j+1] = a[ j ]; }
a[ j+1 ] = target;
}
}
直接挿入法による並べ替えの例を同じ配列でみていきます。図の中で、↑targetが示すのが現在対象となっている要素です。→の左側にある要素がその要素を入れるために1つ後ろにずらされます。枠で囲まれた範囲が、整列が終わった範囲を示します。
直接挿入法のソーティングの様子:
19 64 3 30 10 39 20 53
↑target
19→64→3 30 10 39 20 53
↑target
3 19 64→30 10 39 20 53
↑target
3 19→30→64→10 39 20 53
↑target
3 10 19 30 64→38 20 53
↑target
3 10 19 30→38→64→20 53
↑target
3 10 19 20 30 38 64→53
↑target
整列法における比較回数と交換回数の比較
ArrayListを使って上記の3つの整列法を実現するメソッドを作成し、利用して見なさい。
再帰呼出し(Recursive Call)とは、あるメソッドから、同じメソッドを直接(あるいは間接的に)呼び出すことを指します。 この場合、呼び出されるメソッドは再帰呼出しに対応していないといけません。 多くの場合は、仮引数を必要とし、その引数の値に応じて、一般的に、次のように処理を分けて考えます。
基底レベル…それ以上は、再帰的に呼び出されないレベル、このレベルの処理を考える
それ以上のレベル…再帰的な呼出しがどこかに入る、前後の処理を考える
たとえば、インスタンス変数に値を足していくことを考えます。
int sum; // インスタンス変数
public void start( ) {
sum = 0; // 最初は0に初期化
adder( 10 ); // レベル10で呼出し開始
}
void adder( int level ) {
if ( level <= 1 ) { // 基底レベル(levelが1以下だったら)
sum = sum + level;
printLine( "Sum " + sum + " at the level " + level );
} else { // それ以上のレベル
sum = sum + level;
printLine( "Sum " + sum + " at the level " + level );
adder( level - 1 ); // レベルを1つ小さくして再帰呼出し
}
}
最初の呼び出されるときの実引数が4の場合、以下の図のように引数が渡されていきます。
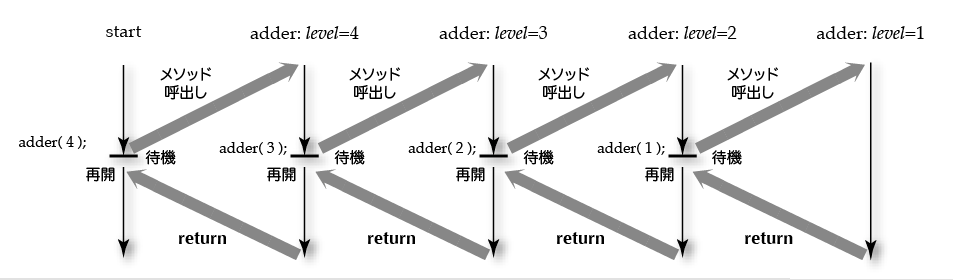
さて、このプログラムを実行してみると次のように表示されます。
Sum 10 at the level 10 Sum 19 at the level 9 Sum 27 at the level 8 Sum 34 at the level 7 Sum 40 at the level 6 Sum 45 at the level 5 Sum 49 at the level 4 Sum 52 at the level 3 Sum 54 at the level 2 Sum 55 at the level 1
これは、再帰呼出しを使わなくても、以下のように繰返しで記述しても同じ結果が得られます。
int sum;
public void start( ) {
sum = 0;
int level = 10;
while ( level >= 1 ) {
sum = sum + level;
printLine( "Sum " + sum + " at the level " + level );
level = level - 1;
}
}
すなわち、ある意味で繰返しと再帰呼出しは同じものと考えることができます。 また、以下のような定理が存在していますが、再帰で考えるのが面倒な場合は、繰返しで実現することが多いと 思われます。
すべての繰返しは、再帰呼出しで実現できる(たぶん逆もあり)
上記のプログラムを実際に入力して描画してみましょう。クラス名はPracticeH409にて。
しかしながら、再帰呼出しを使うと、タートルグラフィックスにおいては、複雑な図形を僅かな量の プログラムで記述することができます。 例として、木のような形を描画して見ましょう。まず、基底レベルを考えます。 基底レベルでする処理は、「Vの字を描くもの」です。 右側の斜線を描いて、左側の斜線を描きます。 プログラムの該当する部分は、以下のような感じになります。
turtle.rotate( 20 ); // 20度右に傾けて turtle.forward( 40 ); // 斜線を描いて turtle.back( 40 ); // 戻ってくる turtle.rotate( -40 ); // 左に40度傾けて turtle.forward( 40 ); // 斜線を描いて turtle.back( 40 ); // 戻ってくる turtle.rotate( 20 ); // 垂直に上を向いておしまい
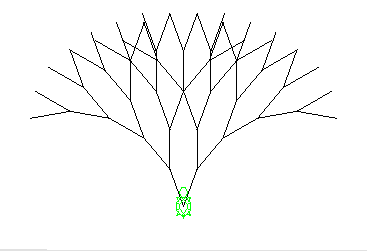
これが基底になるように、プログラムを記述してみます。再帰呼出しの挿入ポイントは、forwardで描いた先です。 そこに更に、同じものを描くように再帰呼出しを入れます。以下のプログラムの断片では、インスタンス変数と startメソッド、およびdrawTreeメソッドを記述しています。その下の図のような木が描けました。
Turtle turtle;
public void start( ) {
turtle = new Turtle( this );
drawTree( 5 );
}
void drawTree( int level ) {
if ( level <= 1 ) { // 基底レベル
turtle.rotate( 20 );
turtle.forward( 40 );
turtle.back( 40 );
turtle.rotate( -40 );
turtle.forward( 40 );
turtle.back( 40 );
turtle.rotate( 20 );
} else { // それ以上のレベル
turtle.rotate( 20 );
turtle.forward( 40 ); // 右の先端に行かせる
drawTree( level-1 ); // 再帰呼出し、ただし、レベルを一つ下げる
turtle.back( 40 );
turtle.rotate( -40 );
turtle.forward( 40 ); // 左の先端に行かせる
drawTree( level-1 ); // 再帰呼出し、ただし、レベルを一つ下げる
turtle.back( 40 );
turtle.rotate( 20 );
}
}
上記のメソッドは、基底レベルとそれ以上のレベルで、ほとんど同じことをしています。 プログラムが長くなるので、逆に条件分岐で再帰呼出しをするかどうか、途中に入れるように drawTreeメソッドを記述してみました。これで、プログラム的にだいぶ短くなりました。
void drawTree( int level ) {
turtle.rotate( 20 );
turtle.forward( 40 );
if ( level > 1 ) { drawTree( level-1 ); } // レベルが1よりも大きいときは再帰呼出し
turtle.back( 40 );
turtle.rotate( -40 );
turtle.forward( 40 );
if ( level > 1 ) { drawTree( level-1 ); } // レベルが1よりも大きいときは再帰呼出し
turtle.back( 40 );
turtle.rotate( 20 );
}
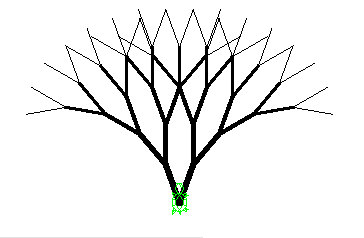
次にレベルに応じて、線の太さを変えてみます。だんだん先に行くに従って、レベルが低くなります から、線が細くなります。再帰呼出しをして戻ってきたら、線のレベルの元に戻します。 線のレベルを戻す文を外に出してありますが、条件分岐のブロックの中に入れても構いません。 drawTreeメソッドの記述を下に示します。 このように太さを変えてみると、その下の図のようになりました。
void drawTree( int level ) {
turtle.setPenWidth( level ); // レベルに応じた太さを設定
turtle.rotate( 20 );
turtle.forward( 40 );
if ( level > 1 ) { drawTree( level-1 ); }
turtle.setPenWidth( level ); // そのレベルに応じた太さを再設定
turtle.back( 40 );
turtle.rotate( -40 );
turtle.forward( 40 );
if ( level > 1 ) { drawTree( level-1 ); }
turtle.setPenWidth( level ); // そのレベルに応じた太さを再設定
turtle.back( 40 );
turtle.rotate( 20 );
}
今度は、線の長さをレベルに応じて変えてみます。このようにすると、 最初はレベルが高いので長い線が描かれますが、レベルが低くなるに従って、 線の長さが短くなります。自然の木に少し近いようになります。なお、線の長さは、レベル×10ドット という形にしました。drawTreeメソッドの記述を下に示します。 レベル5で呼出しを始めると、その下の図のようになりました。
void drawTree( int level ) {
turtle.rotate( 20 );
turtle.forward( 10*level ); // レベルに応じて長さを変える(右側)
if ( level > 1 ) { drawTree( level-1 ); }
turtle.back( 10*level ); // その分だけ戻る
turtle.rotate( -40 );
turtle.forward( 10*level ); // レベルに応じて長さを変える(右側)
if ( level > 1 ) { drawTree( level-1 ); }
turtle.back( 10*level ); // その分だけ戻る
turtle.rotate( 20 );
}
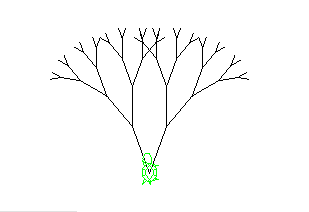
レベルに応じて、色を変えるのも良いかも知れません。今度は、基底レベルに達したら、 赤い実を描くようにしてみました。実は単なる正30角形です。 実を描いたら黒色に戻すようにしています。 メソッド名も少し変更して、「drawFruitTree」としました。 その下にどのような木が描けたのかを表示しました。
void drawFruitTree( int level ) {
if ( level <= 1 ) { // 基底レベル
turtle.setPenColor( Red ); // 赤色にして
turtle.rotate( -84 ); // 左に回転させて
for ( int i=0; i < 30; i++ ) { // 実を描く
turtle.forward( 3 );
turtle.rotate( 12 );
}
turtle.rotate( 84 ); // 回転した分戻す
turtle.setPenColor( Black ); // 黒に戻す
} else { // それ以上のレベル
turtle.rotate( 20 );
turtle.forward( 10*level ); // 枝の長さはレベルに応じて変える
drawFruitTree( level-1 );
turtle.back( 10*level );
turtle.rotate( -40 );
turtle.forward( 10*level );
drawFruitTree( level-1 );
turtle.back( 10*level );
turtle.rotate( 20 );
}
}
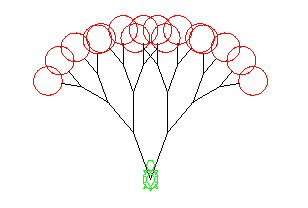
上記のプログラムを実際に入力して描画してみましょう。クラス名はPracticeH410にて。
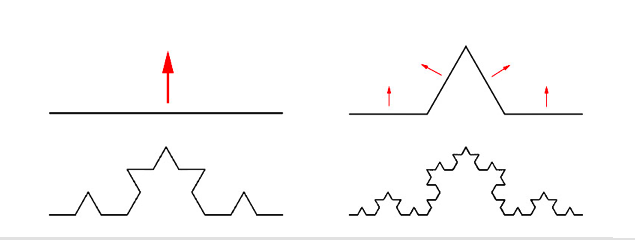
コッホ曲線は、基底においては単なる線を描きます。ところが、次のレベルでは、それを3つの線分に分けて、 真ん中に山を作ります。それぞれの線分に対して、同じように山を作っていったら、下の図のようになります。 かなり有名な曲線です(折れ線だと思うのですが、あるレベル以上になると曲線のように見えてくるので、「曲線」という名前がついています)。 クラス名はKochCurveにて。
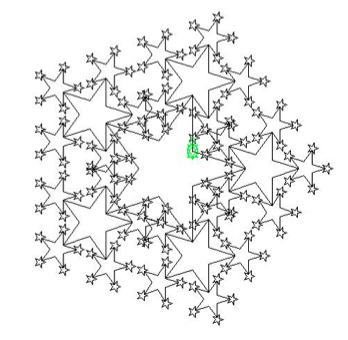
星のそれぞれの端(5つあります)に来ましたら、そこで、より小さな星を描きます。これを再帰的に繰り返すと以下のような図になります。 これは中央の星を中心にして、4レベルまで描画したものになっています。クラス名は、RecursiveStarsにて。
・基底レベル…その演算の元となるような値を返す
・それ以上のレベル…nのときと、n-1のときの関係を再帰呼出しを使って記述する
long factorial( int n ) {
if ( n <= 1 ) { return 1; }
else { return n * factorial( n-1 ); }
}
int summetion( int n ) {
if ( n <= 0 ) { return 0; }
else { return n + summetion( n-1 ); }
}
上記のメソッドを用いて、与えられた数の階乗と(1からのその数までの)総和を求めるようなプログラムを作成します。
int fibonatti( int n ) {
if ( n <= 0 ) { return 0; }
else if ( n == 1 ) { return 1; }
else { int sum = fibonatti( n-1 ) + fibonatti( n-2 ); }
}
上記のメソッドを用いて、100個までのフィボナッチ数を端末に出力するようなプログラムを作成します。
| <<Functions | ⋏ Return to Columns | >>Integers |