Logical Thinking and Programming in 2012 Spring
Minohara Class

Home >> Lecture 11

第11回 実数と関数

実数の指数表現

実数では、指数表現が可能です。eまたはEのあとに、10のべき乗数を書きます。 


	指数表現を使った実数の例：	45.6e9		3.14159E-19		5.5e+4

指数表現とは、以下のように、基数（ここでは10）の何乗というものを掛け合わせた 実数の表現形式のことで、非常に大きい数や小さい数などを表現するときに用います。

　
通常の書き方　指数表現JavaScriptでの指数表現
0.00000567→5.67×10-6→5.67e-6
123000000→1.23×108→1.23e8

たとえば、「1.23×108」という表現ですが、この「1.23」の部分を仮数（Mantissa）と呼び、「8」の部分を指数（Exponent）と呼びます。また、このように0が少なくなるように指数表現を使って桁あわせを行なうことを、実数の正規化（Normalization）と呼んでいます。IEEE-754規格で表現されているJavaScriptの実数定数でも、限られたビットサイズで、非常に小さな数から大きな数を表すために、内部的に正規化を行なっています。

JavaScriptによる実数の表示は、なんとなくお任せ的で、0が一杯になるときは、指数表現されます。そうではないときは、普通に表示されます。

		
	document.write( 45.0 );		//　45.0と表示されます
	document.write( 0.00000032 );	//　3.2e-7と表示されます
	document.write( 55e+20 );		//　5.5e+11と表示されます

Globalオブジェクト

厳密には関数とは異なるのですが、関数と同じように使う事ができるオブジェクトにGlobalオブジェクトがあります。Globalオブジェクトでは、プログラミングを行う上で重要な機能を提供しています。例えば、今までに使ったparseInt()などがそうです。以下にGlobalオブジェクトの機能を挙げます。

メンバ 意味
parseInt(str) 文字列strを整数に変換する。小数点以下は切り捨てる。
parseFloat(str) 文字列strを実数に変換する。
String(val) valを文字列に変換する。
Number(val) valを数字に変換する。

他にもたくさんのメンバがありますので、自分でも調べてみてください。

Mathオブジェクト

Globalオブジェクト同様に厳密には関数ではないのですが、三角関数や平方根など、数学に関わる演算機能を提供しているものにMathオブジェクトがあります。例えば、Math.abs(数値)とすることによって、数値の絶対値を得ることができます。数値は数字リテラルでも変数でも式でも構いません。下記に主要なMathオブジェクトの機能を挙げておきます。メンバがabs(num)の時には、先ほどのようにMath.abs(num)と記述します。

メンバ 意味
abs(num) numの絶対値を求める。
ceil(num) numの小数点以下を切り上げる。
floor(num) numの小数点以下を切り捨てる。
round(num) numをの小数点以下を四捨五入する。
max(num1, num2) num1、num2のうち大きい数を求める。
min(num1, num2) num1、num2のうち小さい数を求める。
pow(num1, num2) num1のnum2乗を求める。
sqrt(num) numの平方根を求める。
exp(num) 指数関数。eのnum乗を求める。
log(num) numの自然対数を求める。
sin(num) サインを求める。numはラジアン。
cos(num) コサインを求める。numはラジアン。
tan(num) タンジェントを求める。numはラジアン。
random( ) 0〜1未満の乱数を返す。

上記の中でrandom()だけは、引数をとらないちょっと風変わりなものになっています。random()は、何も無いところから0〜1未満の乱数を生成します。乱数というのは毎回変わる適当な値です。例えば、「n = random()」のようにすると、nには0〜1未満の値(0.1や0.2345)が入ります。

また、Mathオブジェクトには定数も設定されています。これも関数とは違いますが、以下に挙げておきます。例えば、円周率πを使いたい場合には、プログラムの中で「3.1415...」と書く代わりに「Math.PI」と書くことができます。

メンバ 意味
PI 円周率π。
E 自然対数の底。あるいはネイピア数e。 
var theta = Math.sin( 30 * Math.PI / 180.0 );
var number = Math.floor( 23.454 );
function frac( num ) {
	return num - Math.floor( num );
}
var p = Math.pow( 3, 5 );

対数を使って掛け算と割り算を、足し算と引き算で計算することができます。 

var   num1 = 56.7;
var   num2 = 43.1;
var   lognum1 = Math.log( num1 );
var   lognum2 = Math.log( num2 );
var   logmulti = lognum1 + lognum2;
var   logdiv = lognum1 - lognum2;
var   multi = Math.exp( logmulti );
var   divide = Math.exp( logdiv );

実数の誤差

JavaScriptの実数に関しては、17桁程度の有効桁数しかありません。 これを超えるような桁数を要求する演算を施した場合に、誤差が発生します。 ただし、小数部を10進数から2進数に変換するときに、循環小数になることが 多いので、小数部が循環小数になってしまった場合、17桁以下でも誤差が 発生します。


	a = 4.321 * 100;
	// 432.1が正解ですが、432.099999999999996となります
	// Channel Jより

JavaScriptでは内部的には、実数を有限のデジタル情報として実数を表しています。 そのために、本来アナログ情報である実数を表し切れない場合があるのです。本来のアナログ情報である実数とデジタルで表した場合の実数との差を誤差（Error）と呼んでいます。 実数の計算には、誤差がつきものなのです。JavaScriptでは、実数を64bitの精度で表していますので、従来のプログラミング言語で頻繁に起きていた誤差がかなり少なくなっています。しかし、上のように単純な割り算・掛け算でも誤差が入り込んできます。

以下に誤差のいくつかの類型を見ていきましょう。

☆丸め誤差

JavaScriptでは、有限のビット数でしか実数を表わせませんので、どこかで桁を打ち切るしかありません。このときに、行なわれる四捨五入や切り捨てなどの操作によって真の数とコンピュータ上で表された数が異なるために起こる誤差を丸め誤差（Round Error）と呼んでいます。

☆情報落ち

JavaScriptの実数の計算の中入り込んでくる誤差を情報落ちと呼んでいます。誤差の多かった時代には、なるべく情報落ちを少なくするような形で実数の計算が行なわれていました。情報落ちが発生しやすいときはどんなときでしょうか？経験的に、次のようなことがよく言われています。

「違うオーダー（大きさ）の数を足し算したり、引き算したりすると誤差が発生する」

たとえば、非常に大きな数と小さな数を足し合わせることを考えてみてください。100,000,000に1を足すときは、100,000,000であっても100,000,001であっても、数の大きさ的には大きくは変わりません。同じように、有限のデジタル情報として実数が表されるとき、小さな差は丸められてしまいます。この丸めが情報落ちを発生する原因となっています。実数で計算を行なう場合は、このような大きさが著しく違う数を足したり、引いたりすることを避けなければなりません。


	document.write( 1.234e67 + 1.234e-45 );		// ２番目の1.234e-45が足されたことが無視されています。

☆桁落ち

桁落ちとは、値がほぼ等しく丸め誤差をもつ数値どうしの減算を行った場合、有効数字が減少することを指します。

☆打ち切り誤差

無理数の√２や、πなどを考えてみてください。JavaScriptでは、有限のビット数でしか実数を表わせませんので、どこかで計算を打ち切るしかありません。このようにして入り込んでくる誤差を打ち切り誤差（Drop Error）と呼んでいます。以下のJavaScriptのプログラムの断片は、それらを表示するものです。ここで表示された範囲だけしか、計算に入れていません。それ以下の小数部は無視されています

。 

	document.write( Math.PI );			// 3.141592653589793
	document.write( Math.sqrt( 2.0 ) );	// 1.4142135623730951

JavaScriptによるcanvas描画の基本（復習）

canvas要素は、Webページにプログラムによる描画領域を確保するための要素です。前回の繰り返しになりますが、次のように記述します。この記述では200×200の描画領域を確保しています。タグで囲まれた「四角形を描画する領域」は、もしもcanvas要素をサポートしていないブラウザでこのページが表示された場合に代替として表示される文字列です。最新のFirefoxやSafariなどのブラウザを利用している限りは、このような文字列が表示されることはありません。

<canvas id="canvas" width="200" height="200">四角形を描画する領域</canvas>

キャンバス要素をHTML文書の中に挿入するだけでは、単にページに空間が空くだけになります。この文章の直後に空間が空いていると思いますが、これは上記の記述をこのページに挿入しているためです。実際にcanvas要素を活用するためには、JavaScriptによって描画をすることが必要です。次章以降ではJavaScriptによる描画方法について説明します。

四角形を描画する領域

canvas要素で確保した描画空間にJavaScriptを使って描画をするためには、canvas要素をプログラムの中で取得し、そこから更に描画コンテクストを取得する必要があります。

var canvas = document.getElementById('canvas');
var ctx = canvas.getContext('2d');

上記は前回のcanvas要素の紹介で出てきた四角を描画するプログラムの一部分です。1行目は見慣れた記述だと思いますが、ここでcanvas要素を取得しています。2行目は新しく出てきた記述です。この行で二次元描画用のコンテクストを取得しています。コンテクストというのは解りにくいかもしれませんが、描画を行うにあたり、どのような座標を使うのか、四角や円などどのような図形を指定することが出来るのかなどを定義したものです。つまり、ここでは「'2d'」と指定することによって、二次元描画コンテクストを取得しています。二次元があるということは「'3d'」と書くと三次元描画もできるのかと思いますが、残念ながら現在のところ唯一使える描画コンテクストは「'2d'」のみです。将来的には三次元描画コンテクストも使えるようになるかも知れません。

キャンバスの描画コンテクストを取得すると、そこに存在している幾つかのプロパティを変更することができます。例えば、線の色や太さなどがそうです。JavaScriptで線の太さを変更するためには、描画コンテクストctxを取得した後に(変数名は「ctx」でなくとも問題ありませんが、ここでは便宜上、上記の続きでとみなして「ctx」を使います)、lineWidthプロパティを変更します。また、線の色を変更するためにはstrokeStyleプロパティを変更します。更に、塗りつぶしを行う場合の色は、fillStyleプロパティを変更することによって指定が可能です。

次のプログラムを見てください。7行目から9行目までで線の太さ、色、塗りつぶしの色を指定しています。また、11行目と12行目でそれぞれ、塗りつぶした四角を描画し、四角の枠を描いています。

<canvas id="canvas" width="200" height="200">四角形を描画する領域</canvas>
 
<script>
var canvas = document.getElementById('canvas');
var ctx = canvas.getContext('2d');

ctx.lineWidth = 10.0;
ctx.strokeStyle = "black";
ctx.fillStyle = "lightgrey";

ctx.fillRect(50, 50, 100, 100);
ctx.strokeRect(50, 50, 100, 100);
</script>

☆練習問題11-1

  1. 上記のプログラムを実行してみなさい。
  2. ctx.fillRect()の行とctx.strokeRect()の行を入れ替え、何が起きるかを確認しなさい。

実数の関数を用いたcanvas描画

また、描画においては、より複雑な図形を描画するためにパスという概念があります。これは、いろいろな描画メソッドを組み合わせて図形を描く時に使われるものです。例えば、六角形を描画するメソッドは二次元描画コンテクストには存在しませんが、次のようにすることによって六角形を描くことができます。ここで、beginPath()メソッドからclosePath()メソッドまでがパスを定義している部分になります。その中でmoveTo()メソッド(ペン先を上げた状態で座標に動かす)や、lineTo()メソッド(ペン先を下ろした状態で指定した座標に動かす。つまり、現在ペン先がある所から指定した座標まで直線を引く。)を使って六角形を描き、その上でfill()メソッドによって塗りつぶし、また、stroke()メソッドによって直線を引いた部分に色をつけています。fill()メソッドやstroke()メソッドによって色をつけるまでは、実際には目に見える形にはならないことに気をつけてください。

<canvas id="canvas" width="200" height="200">六角形を描画する領域</canvas>
 
<script>
var canvas = document.getElementById('canvas');
var ctx = canvas.getContext('2d');

ctx.translate( 100, 100 );  // 中心点の座標を移動
var r = 80;   // 半径

ctx.lineWidth = 3.0;
ctx.strokeStyle = "black";
ctx.fillStyle = "lightgrey";

ctx.beginPath();
ctx.moveTo( Math.sin(0 * 2 * Math.PI / 6) * r, Math.cos(0 * 2 * Math.PI / 6) * r);
for (var i=1; i <= 6; i = i + 1 ) {
	ctx.lineTo( Math.sin( i * 2 * Math.PI / 6) * r, Math.cos( i * 2 * Math.PI / 6) * r);
}
ctx.fill( );
ctx.stroke( );
ctx.closePath( );
</script>

また、ここで気をつけるべきことがもう一つあります。通常のグラフでは、X軸は左から右、Y軸は下から上に向かって数字が増えていきますが、canvas要素で描画をする場合にはY軸は上から下に数字が大きくなります。座標を計算する場合はこの点に注意してください。

canvasの座標系

canvasの座標系

☆練習問題11-2

  1. nを入力して、n角形を描画するようなプログラムを作成しなさい。
    2. n角形の描画

    n角形の描画

  2. 下記のような星印を描きなさい。
    3. 四角形を描画する領域

指数関数の曲線

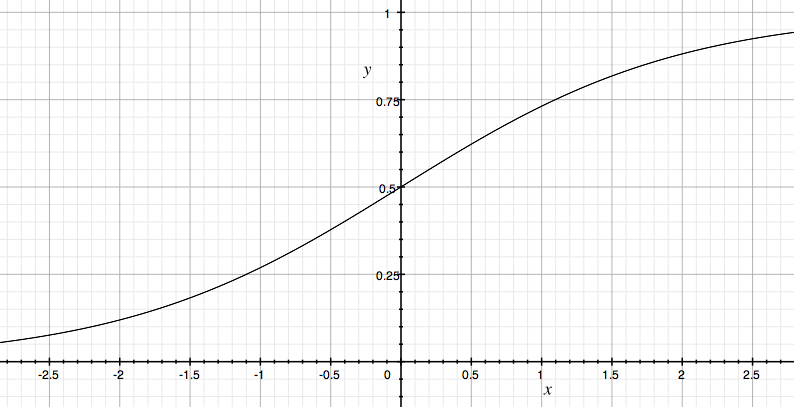
シグモイド関数（sigmoid function）は、 次のような数式で表される実関数です。値域は、0〜1になります。なお、aをゲイン (gain) と呼びます。 このゲインは、横方向の幅（傾き）を規定するものです。

sigmoid( x ) = 1 / ( 1 + e-ax )

a=1、すなわち、ゲインが1のシグモイド関数を 標準シグモイド関数 (standard sigmoid function)と呼びます。

sigmoid( x ) = 1 / ( 1 + e-x )

シグモイド関数は、(0, 1/2）の点を中心として、点対称であったり、 xを無限小（-∞）にすると、0に近づき、無限大（+∞）にすると 1に近づくという性質があります。

シグモイド関数で表わされた曲線は、ロジスティック曲線（logistic curve）と呼ばれ、 いろいろなところで用いられることがあります。名前だけは覚えておきましょう。

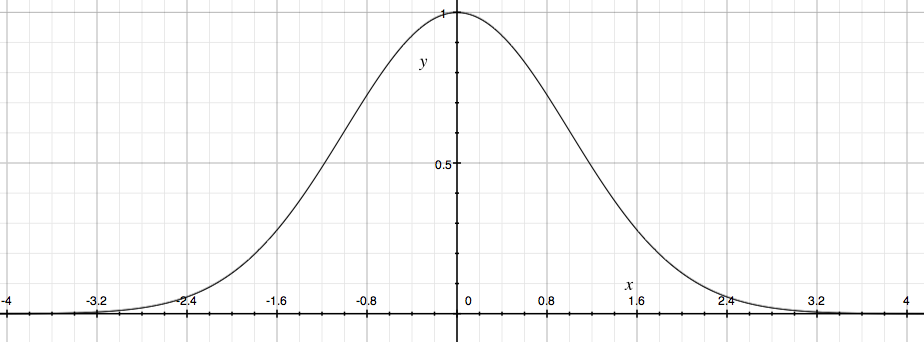
正規分布などで用いられる確率密度関数をもう少し簡単にすると次のような式で記述することができます。 ここで、μは平均で、δは分散を表わします。μは中心になります。δは、横の広がりを示します。

normaldistribution( x ) = e- (x-μ)2/ 2δ2

これもμ=0, δ=1の場合が標準と考えて良いでしょう。

normaldistribution( x ) = e- x2/ 2

☆練習問題11-3

  1. JavaScriptでロジスティック曲線を描いてみましょう。
  2. 確率密度関数のグラフを描いてみましょう。
  3. アルキメデスの螺旋（r=aθ）を描いてみましょう。aは定数です。
  4. 対数螺旋（r=aθ）を描いてみましょう。
  5. リサージュ図形を描いてみましょう。
  6. Lituus（r2θ = a）を描いてみましょう。

二次元配列

表計算のようなことをしようとする場合、これまで使ってきた配列だけでは機能が不足することがあります。例えば、次のようなデータがあるとしましょう。

日付 始値 高値 安値 終値
2011年1月10日 82.690000 83.540000 82.379900 82.940000
2011年1月17日 82.800000 83.489900 81.819900 82.580000
... ... ... ... ...

これは、今年の週毎のドル円の為替データです。このデータを扱うためにはどのようにすれば良いでしょうか? 1つ考えられる方法としては、それぞれのカラムを配列として扱うことです。例えば次のようになります。

var date =  ["2011年1月10日", "2011年1月17日", ...];
var start = [82.690000, 82.800000, ...];
var high =  [83.540000, 83.489900, ...];
var low =   [82.379900, 81.819900, ...];
var end =   [82.940000, 82.580000, ...];

確かにこれでもデータを扱うことはできますが、もう少し良い方法があります。この様な時に使えるのが二次元配列です。二次元配列とは表のように列と行によってデータを格納するための配列です。例えば、次のように記述します。

usdjpy = [
  ["2011年1月10日",82.690000,83.540000,82.379900,82.940000],
  ["2011年1月17日",82.800000,83.489900,81.819900,82.580000],
  ...
];

この例では、日付・始値・高値・安値・終値を1つの行として配列にし、更に週毎にその配列を作っています。つまり「["2011年1月10日",82.69,83.54,82.3799,82.94]」もひつとの配列ですし、それを集めた全体も配列です。上の例ではusdjpyという変数には配列の配列、二次元配列が格納されます。

さて、データを二次元配列に入れる方法は説明しましたが、これはどのようにして使えば良いのでしょうか? 使い方は二次元配列が配列の配列であることが解れば難しくありません。例えば、1行目の2列目を使うためには「usdjpy[0][1]」のようにします。配列は0番目から始まるため、1行目を表す添字は0になりますし、2列目を表す添字は1になります。

<script>
usdjpy = [
  ["2011年1月10日",82.690000,83.540000,82.379900,82.940000],
  ["2011年1月17日",82.800000,83.489900,81.819900,82.580000]
];

document.write(usdjpy[0][1]);
</script>

実際に上のプログラムを実行した結果は、下のようになります。

☆練習問題 11-4

  1. http://ipl.sfc.keio.ac.jp/text/pro-2011-9/lib/usdjpy.jsに今年のドル円の為替データを入れた配列を作るプログラムが用意されています。このデータを使って、下のような表を最後まで出力するプログラムを作りなさい。
  2. http://ipl.sfc.keio.ac.jp/text/pro-2011-9/lib/usdjpy.jsのデータを使って始値で折れ線グラフを書きなさい。
    3. ドル円の折れ線グラフ