Home >> Lecture 4
整数は、内部では2進数で表されていますので、直接2進数の各ビットを制御する演算子があります。 これらの演算子はC/C++からの継承になります。 次のようなビット演算が可能になります。
| 名称 | 演算子 | 意味 | 記述例 |
|---|---|---|---|
| 反転 | ~ | ビットごとに反転させます(complement) | ~value |
| ビット論理積 | & | ビットごとに論理積を取ります(and) | a & b |
| ビット論理和 | | | ビットごとに論理和を取ります(or) | a | b |
| ビット排他的論理和 | ^ | ビットごとに排他的論理和を取ります(exclusive or) | a ^ b |
ビット演算子では、1=true, 0=falseという形で考えてみて下さい。 ビット論理積と論理和では、論理値の演算子に対して、1つ記号が少なくなっています。 また、^という演算子は、べき乗を表すのではなく、ビット排他的論理和として使われていますので注意して下さい。
byte x = 14; // 2進数で00001110 System.out.println( ~x ); // 00001110 → 11110001 (10進数では-15) System.out.println( x & 7 ); // 00001110 & 00000111 → 00000110 (10進数では6) System.out.println( x | 5 ); // 00001110 | 00000101 → 00001111 (10進数では15) System.out.println( x ^ 0xb ); // 00001110 ^ 00001011 → 00000101 (10進数では5)
2の補数にする場合は、反転させて、+1します。そうすると符号が反転します。 以下はbyte型(8bit)の変数を使って、31の2の補数表現を計算しています。 内部的には、すべてint型(32bit)で計算していますので、代入するときは、キャストを 使ってbyte型に戻しています。
byte x = 31; // 2進数で00011111 x = (byte)(~x); // 各ビットを反転 2進数で11100000 x = (byte)(x + 1); // 2進数で11100001 → byteで標記すると-31 System.out.println( Integer.toString( x & 0xff ) ); // 下位8bitだけを表示させる
二項ビット演算子で自己参照によって変数の値を変える場合は、次のように代入演算子の省略形があります。
▼二項ビット演算子による代入演算子:
&= ビット論理積と代入の組み合わせ x &= 3 x = x & 3
|= ビット論理和と代入の組み合わせ x |= 10 x = x | 10
^= ビット排他的論理和と代入の組み合わせ x ^= 3 x = x ^ 3
& (bit and)演算を使えば、以下の例のように、値に対して、特定のビットだけを考慮させることができます。 これを通常「マスク(mask)する」と呼びます。 また、| (bit or)演算を使えば、特定のビットを1にすることができます。 これを「ビットを立てる」と呼ぶことがあります。
int x = 49; // 2進数で110001 System.out.println( Integer.toBinaryString( x & 0xffff ) ); // xの下位16bitだけを表示 System.out.println( Integer.toBinaryString( x ^ x ) ); // 同じ値を排他的論理和を取るとクリアされる System.out.println( Integer.toBinaryString( -x & 0xff ) ); // 下位8bitだけを表示させる System.out.println( Integer.toBinaryString( x | 2 ) ); // 2桁目のbitを必ず1にする
| 名称 | 演算子 | 意味 | 記述例 |
|---|---|---|---|
| 算術右シフト(符号付き) | >> | 各ビットを右にn回シフトし、最上位ビットの値は保存されます。 これによって、符号を温存することができます。 | a >> 3 |
| 論理右シフト(符号無し) | >>> | 各ビットを右にn回シフトし、最上位ビットには各シフトごとに0がはいります。 | b >>> n |
| 左シフト | << | 各ビットを左にn回シフトし、最下位ビットには各シフトごとに0がはいります | a << 4 |
通常の算術右シフト算、左シフト算は、右シフト1回で値を半分にし(整数除算の1/2)、 左シフト1回で値を2倍にすると考えておけば良いでしょう。
System.out.println( 33 >> 1 ); // 整数除算で2で割ったのと同じ、16が表示される System.out.println( 15 << 1 ); // 2倍したのと同じ、30が表示される System.out.println( 5 << 4 ); // 24 = 16倍したのと同じ、80が表示される System.out.println( 429 >> 3 ); // 23 = 8で割ったのと同じ、53が表示される
ここまでで、 2文字以上連続(間に空白を入れてはいけない)演算子(およびコメントなどの記号も含む)がほぼ出揃いました。 以下にその一覧表を示します。 これらの演算子では、記号の間に演算子を入れてしまうと、コンパイラエラーになってしまいます。 また、\uや0xでは直後に16進数を書かないといけません。
|
Integer.toBinaryString( )は、1となっている最上位ビットまでしか表示しません。 これを指定された桁数上位bitの0も含めて表示するアプリケーションを作成しなさい。
これまで出てきた演算子の優先順位の一覧です。上から順番に優先度が高くなっています。 同じ優先順位の演算子は、左結合性を持ちます。ただし、代入演算子だけは、右結合性を持ちます。
|
コンピュータは、実数に関しては概算でしか計算しません。実数を表わすビット数が限られているからです。 ここでは、誤差について説明します。「コンピュータが殊に実数に関しては、いつでも正確な計算をしない」ということを 憶えてください。
たとえば、1/3.0 * 3.0は、通常は1.0になります。 3.0で割る操作を100回繰り返して、もう一度100回3.0倍する操作を繰り返しても、理論的には同じことで結果は1.0になるはずです。 それでは実際に次のようなプログラムの断片の部分を実行させてみましょう。
double x = 1.0;
int n=1;
while ( n <= 100 ) { x=x/3.0; n = n + 1; }
while ( n > 1 ) { x= x*3.0; n = n - 1; }
System.out.println( "result is "+x );
ところが、表示は次のようになりました。1.0にはなっていません。どうしてでしょうか?
result is 1.0000000000000009
Javaでは内部的には、有限のデジタル情報として実数を表しています。 そのために、本来アナログ情報である実数を表し切れない場合があるのです。 本来のアナログ情報である実数とデジタルで表した場合の実数との差を誤差(Error)と呼んでいます。 実数の計算には、誤差がつきものなのです。Javaでは、実数を64bitの高精度で表していますので、 従来のプログラミング言語で頻繁に起きていた誤差がかなり少なくなっています。 しかし、上のように単純な割り算・掛け算も繰り返して行なわせると誤差が入り込んできます。
int n=100000000;
double delta = 1.0/n;
double result = 0.0;
for ( inti=1; i <= n; i++ ) { result += delta }
System.out.println( "result is "+result );
以上のプログラムは、1を1億で割ったものを、0に1億回足すプログラムになっています。 答えは、1.0になるはずですが、実際には以下のようになります。これも誤差のなせる結果です。
result is 1.0000000022898672
以下に誤差のいくつかの類型を見ていきましょう。
Javaでは、有限のビット数でしか実数を表わせませんので、どこかで桁を打ち切るしかありません。 このときに、行なわれる四捨五入や切り捨てなどの操作によって真の数とコンピュータ上で表された数が異なるために起こる誤差を 丸め誤差(Round Error)と呼んでいます。 特に10進数で通常に表すことができる小数も、2進数にするとすぐに循環小数になってしまいますので、丸め誤差が 出やすくなっています。0.1などは、2進数では循環小数になってしまいますので、次のような計算をすると、 丸め誤差が発生しているのがわかります。
System.out.println( 0.1+0.2 ); // 0.30000000000000004と表示されます System.out.println( 0.1+0.7 ); // 0.7999999999999999と表示されます System.out.println( 0.3-0.2 ); // 0.09999999999999998と表示されます
Javaの実数の計算の中入り込んでくる誤差を情報落ちと呼んでいます。 誤差の多かった時代には、なるべく情報落ちを少なくするような形で実数の計算が行なわれていました。 情報落ちが発生しやすいときはどんなときでしょうか?経験的に、次のようなことがよく言われています。
「違うオーダー(大きさ)の数を足し算したり、引き算したりすると誤差が発生する」
たとえば、非常に大きな数と小さな数を足し合わせることを考えてみてください。 100,000,000に1を足すときは、100,000,000であっても100,000,001であっても、数の大きさ的には大きくは変わりません。 同じように、有限のデジタル情報として実数が表されるとき、小さな差は丸められてしまいます。 この丸めが情報落ちを発生する原因となっています。 実数で計算を行なう場合は、このような大きさが著しく違う数を足したり、引いたりすることを避けなければなりません。
System.out.println( 1.234e67 + 1.234e-45 ); // 2番目の1.234e-45が足されたことが無視されています。
また、float型をdouble型に変換しても、すぐに情報落ちが起こります。たとえば、プログラム上で次の表示をさせてみて下さい。
System.out.println( (double)0.3f );
これは、単精度実数を倍精度実数に変換しただけなのですが、表示は「0.3」ではなくて、次のようになります。 これだけみても、情報落ちが単精度実数で特に酷いのがわかると思われます。
0.30000001192092896
桁落ちとは、値がほぼ等しく丸め誤差をもつ数値どうしの減算を行った場合、有効数字が減少することを指します。 たとえば、「1.23456789×102-1.23456780×102」を計算すると、計算結果は 「9.0×10-6」となり、有効桁数が1桁になってしまうような場合のことを差します。 ちなみ、上記の計算をJavaでしてみると、丸め誤差が発生しますので、以下のような値になります。
System.out.println( 1.23456789e2-1.23456780e2 ); // 9.000000005698894E-6と表示されます
上記の情報落ちを、いくつかの計算で確かめてみましょう。クラス名は、Practice0801とします。
無理数の√2や、πなどを考えてみてください。 Javaでは、有限のビット数でしか実数を表わせませんので、どこかで計算を打ち切るしかありません。 このようにして入り込んでくる誤差を打ち切り誤差(Drop Error)と呼んでいます。 以下のJavaのプログラムの断片は、それらを表示するものです。 関数については、次の節で説明します。 ここで表示された範囲だけしか、計算に入れていません。それ以下の小数部は無視されています。
System.out.println( Math.PI ); System.out.println( Math.sqrt( 2.0 ) );
BlueJでの環境では、以下のように表示されました。だいたい17桁程度です。
3.141592653589793 1.4142135623730951
上記の表示は標準の桁数しか表示されません。そこで、繰返しでSystem.out.printfメソッドを使って小数部が どこまで詳しく表示されるかどうか見て下さい。クラス名は、Practice0403とします。
上記の誤差について結論を述べると次のようなことになります。
コンピュータは実数に関しては、必ずしも正確な計算をするとは限らない。
プログラマが注意してなるべく、本来の値(真数)に近づくように計算をさせる必要がある。
たとえば、誤差を含んだ実数において、「等しい」というのは、機能しない場合があります。 次のような条件式を持ったプログラムについて考えてみましょう。xは実数型の変数とします。
if ( x == 10.3 ) { ..... }
このような記述は、ほとんどの場合うまく機能しません。誤差が含まれるので、10.3の値になる可能性が 少ないからです。実数の場合には、等価性を求めるときには「ある範囲内に入っている」という記述をします。 たとえば、上記のような場合は、一定の誤差が含まれる範囲を指定しておき、その範囲内に入っていたら、 同じであると見なすという形で記述します。
double range = 0.01; // 誤差の許容範囲を0.01としています。
if ( x >= 10.3 - range && x <= 10.3 + range ) { ..... }
Mathクラスには、数学上使う便利な関数がメソッドとして用意されています。 ここでは、最低限の三角関数とその他の良く使うものだけに限り紹介します。
| 分類 | 定数またはメソッド | 評価結果の型 | 意味 |
|---|---|---|---|
| 定数 | PI | double | 円周率を表す |
| E | double | 自然対数の底を表す | |
| 整数値 | ceil( 実数 ) | double | その数より大きいか等しい整数と等しい値にする |
| floor( 実数 ) | double | その数より小さいか等しい整数と等しい値にする | |
| rint( 実数 ) | double | その数に最も近い整数と等しい値にする | |
| round( 実数 ) | long | 小数部を四捨五入して整数にする | |
| 三角関数 | cos( 角度 ) | double | cosを求める |
| sin( 角度 ) | double | sinを求める | |
| tan( 角度 ) | double | tanを求める | |
| acos( 底辺/斜辺 ) | double | 底辺と斜辺の比から角度を求める(値域は0〜π) | |
| asin( 直立辺/斜辺 ) | double | 直立辺と斜辺の比から角度を求める(値域は-π/2〜π/2) | |
| atan( 直立辺/ 底辺 ) | double | 直立辺と底辺の比から角度を求める(値域は-π/2〜π/2) | |
| atan2( 実数 , 実数 ) | double | 2つの実数をy、x座標として角度を求める | |
| hypot( 直立辺 , 底辺 ) | double | 直立辺と底辺から斜辺の長さを求める | |
| 双曲関数 | cosh( 角度 ) | double | cosh(双曲線余弦)を求める |
| sinh( 角度 ) | double | sinh(双曲線正弦)を求める | |
| tanh( 角度 ) | double | tanh(双曲線正接)を求める | |
| 指数・対数 | exp( 実数 ) | double | 自然対数の底のべき乗を求める |
| pow( 実数, 実数 ) | double | べき乗を求める | |
| log( 実数 ) | double | 自然対数を求める | |
| log10( 実数 ) | double | 常用対数を求める | |
| その他 | abs( 数 ) | double, float, long, int | 絶対値を返してくる |
| max( 数, 数 ) | double, float, long, int | 2つの数のうち大きい方を返す | |
| min( 数, 数 ) | double, float, long, int | 2つの数のうち小さい方を返す | |
| random( ) | double | 0.0以上1.0未満の間で乱数を返してくる | |
| sqrt( 実数 ) | double | 平方根を求める | |
| cbrt( 実数 ) | double | 立方根を求める |
実際にこれらの関数を使って簡単な数式、あるいは代入文を記述してみましょう。
double ceil = Math.ceil( 44.23 ); // ceil = 45.0 double floor = Math.floor( 44.23 ); // floor = 44.0 double closest = Math.rint( 44.23 ); // closest = 44.0 int round = Math.round( 44.23 ); // round = 44 int trunc = (int) 44.23; // trunc = 44
整数への変換で注意しなければならないのは、ceilやfloorなどは、それぞれ負の数の場合は、 絶対値的には異なるような数に変換されるということです。 また、roundとキャスト(このキャストの小数部の切捨ては、一般にはtruncateと呼ばれます)だけは整数に変換されますが、 他のものは関数の計算結果が実数のままであるということにも注意してください。 また、roundは四捨五入ですので、下の例のような形になります。コメントとして書かれているのが、計算結果です。
Math.ceil( 23.45 ) // 24.0 Math.ceil( - 23.45 ) // - 23.0 Math.floor( 23.45 ) // 23.0 Math.floor( - 23.45 ) // - 24.0 Math.rint( 23.45 ) // 23.0 Math.rint( - 23.45 ) // - 23.0 Math.round( 23.45 ) // 23 Math.round( - 23.45 ) // - 23 Math.round( 23.50 ) // 24 Math.round( -23.50 ) // -23 Math.round( 23.55 ) // 24 Math.round( -23.55 ) // -24 (int) 23.45 // 23 (int) - 23.45 // - 23
ceilとfloorの関係、あるいはroundとfloorの関係を示すのに次のような公式が用いられることがあります。 これで、各関数の関係を判断してみてください。
Math.ceil( x ) = - Math.floor( - x ) Math.round( x ) = (int) Math.floor( x + 0.5 )
三角関数、逆三角関数の場合は、角度を指定するときはすべてradian体系(πを基準とする体系)で行なわれます。 通常の360度を使って角度を表す体系はdegree体系と呼ばれています。その間の変換は、次のようになります。 なお、πを指定するときは、JavaではMath.PIと記述します。
radian角度 = degree角度 / 180 * π
例えば 90゜は1/2π
代表的な角度を以下に書き記してみました。
|
これを変換するために、以下の2つのメソッドが用意されています。計算結果は実数です。
Math.toRadians( degree角度 ) … radian角度に変換する
Math.toDegrees( radian角度 ) … degree角度に変換する
実際に、三角関数などを使った式を記述してみましょう。
double radians = Math.toRadians( 60 ); // 60度をradian角度に変換する double bottom = Math.cos( radians ) * 10; // 60度のときの斜辺が10のときの底辺の長さを求める double result = Math.sin( Math.toRadians( 60 ) ); // sin( 60 ) = √3 / 2 を求める double ratio = Math.cos( Math.PI / 3 ); // cos 60 = 1/2 これは斜辺の長さが1のとき double alpha = Math.toDegrees( Math.atan2( 1.0, 1.0 ) ); // x, yの値から角度を求める。alpha = 45度
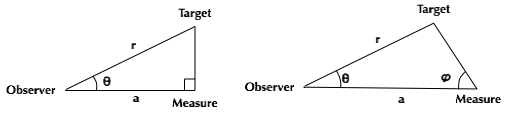
ユーザに三角測量のときに、垂直に立てた測定物差しまでの距離aと、 本当に測定したいものと測定物差しの間の角度θを入力してもらいます。 そして、本当に測定したいものとの距離rを求めるようなプログラムを書いて下さい。クラス名は、 Triangulationです。え?忘れたって?斜辺をrとして、底辺をaとするとcosθ=a/rでしたね。 さて、余裕がある人は、上記の場合は測定したいものと丁度90度を成す角度の位置に測定物差しが 置かれていたのですが、測定物差しの場所からみて、測定者と測定対象の角度がφ度だったときに、 測定者と対象物までの距離rを求めるプログラムを書いてみて下さい。

その他の関数としては、絶対値を求めるようなもの、自然対数関連のもの、べき乗や平方根などがあります。 絶対値以外は、実数に対してしか用意されていないことに注意してください。
int abs = Math.abs( -44 ); // 44 double power = Math.pow( 4, 3 ); // 43 double rand = Math.random( ); // 0.0 <= n < 1.0 double root = Math.sqrt( 2.0 ); // √2 = 1.41421356.... double cubicroot = Math.cbrt( 39.304 ); // 3√39.304 = 3.4
Math.randomは、乱数になっていて、0.0〜1.0の間の適当な実数を発生して返してくれます。 しかし、1.0という値は発生しませんので注意が必要です。 たとえば、サイコロのように1から6までのどれかの整数を得たい場合は、次のように記述します。
int dice = (int)( Math.random( ) * 6 + 1 ); // 1〜6までの乱数を発生
2つの垂直に交差する軸の距離から、2点間の距離を求めて下さい。 r2=x2+y2でした。クラス名は、Pythagorasです。
曲線そのものを描画する場合は、線は、点の動きとして表わされますから、xを変えながら、y座標の位置を求め、 座標の決まった各点を描いていけばいいように思えます。 ところが、Javaでは点を描くというメソッドがありません。また一般的にも点で描くということは行なわれていません。 一般的は、短い直線で曲線を描くことが行なわれています。つまり、折れ線で曲線を近似しようということになります。
線を描くにはdrawLineメソッドを使うのですが、始点と終点の2つの点の座標が必要でした。 2つの点を決めるために、新たに求める1つの点は計算で求めるとして、 もう1つの点は前に計算した点の座標を別の変数(以下の記述では、lastxとlasty)で覚えておくことにします。 1つ前の点から、現在の点まで線を引くようにします。 そこで座標を計算して線を描いた後に、その値を次のように更新するようにします。
lastx = x; lasty = y;
このように常に一つ前の点の座標を別の変数に覚えておけば、そこから、現在までの点の座標(xとy)を計算で 求め、2つの点の間に線を引くことができるでしょう。
パラメータ形式で表わされる曲線のことを、パラメトリック曲線(Parametric Curve)と呼びます。 この曲線を、以上のような形でn本の折れ線で近似するためには、つぎのプログラムの断片で描くことになります。 ここで、x = f( t )やy=g( t )とは、媒介変数tを使った何らかの計算式で、xやyが描かれるということを示しています。
▼パラメトリック曲線の描画方法:
double delta = 1.0 / n; // 媒介変数tを0〜1の間で移動させるときのステップ間隔 double t = 0.0; int lastx = f( 0 ), lasty = g( 0 ); for ( int i=1; i <= n; i++ ) { t += delta; int x = f( t ), y = g( t ); g.drawLine( lastx, lasty, x, y ); lastx = x; lasty = y; }
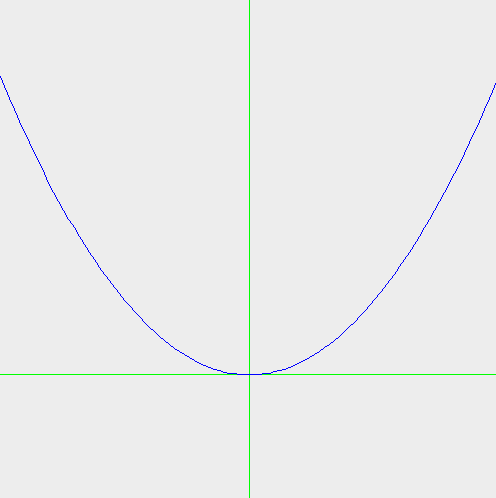
この方法で、2次関数の放物線を折れ線で表示してみましょう。ここでは、ウィンドウの座標への変換も考慮すると、 関数fとgは、次のように記述できるのではないでしょうか。
size = 200; // tの定義域の大きさ f( t ) = t * size - size/2 + centerx // xの変化範囲が0を中心とする-size/2からsize/2 // のsizeの範囲なのでこのような式になる、+centerxは座標変換用 g( t ) = - ( t*size - size/2) * (t*size - size/2) * 0.015 + centery
centerxとcenteryは、座標軸の原点の座標のグラフィックス上のx, y座標です。 たとえば、以下のようにしてアプレットのグラフィック描画領域の幅と高さから求めることができます。
int centerx = getWidth( ) / 2; // 描画領域の幅の半分 int centery = getHeight( ) / 2; // 描画領域の高さの半分
実際のアプレットのプログラムとして、記述してみましょう。 たとえば、折れ線の数nを100とします。型変換も含めると次のように記述できます。 paintメソッドの部分だけを記述しました。
public void paint( Graphics g ) {
int n = 100;
int size = getWidth( ); // 描画領域の幅がサイズ
double scale = 300.0 * 4 / size / size; // y方向の最大の高さは300とする
int centerx = getWidth( )/2, centery=getHeight( ) * 3 / 4;
double delta = 1.0 / n;
double t = 0.0;
int lastx = -size/2+centerx;
int lasty = (int)(-(size/2)*(size/2.0)*scale)+centery;
for ( int i=1; i <= n; i++ ) {
t += delta;
int x = (int)( t * size ) - size/2 + centerx;
int y = -(int)((t*size-size/2) * (t*size-size/2) * scale) + centery;
g.drawLine( lastx, lasty, x, y );
lastx = x;
lasty = y;
}
}
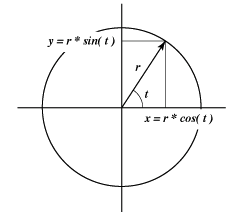
同じようにパラメトリック曲線の描画手法を用いて、三角関数のcosとsinを使ってx、y座標を計算していけば、 円が描けます。以下の式でrは半径、tは中心の角度とします。
x = r * Math.cos( t ) + centerx; y = r * Math.sin( t ) + centery;
public void paint( Graphics g ) {
int x, y, lastx, lasty;
int centerx = 100, centery = 100;
int radius = 80;
g.drawLine( 0, centery, 200, centery ); // 横軸
g.drawLine( centerx, 0, centerx, 200 ); // 縦軸
lastx= radius + centerx;
lasty= centery;
for (int i=1; i<=360; i++ ) {
double radian = Math.toRadians( i );
x = (int) (Math.cos( radian ) * radius )+ centerx;
y = (int) (-Math.sin( radian ) * radius ) + centery;
g.drawLine( lastx, lasty, x, y );
lastx = x;
lasty = y;
}
}
オシロスコープという機械では、2つの波形の位相や比率を知ることができます。 そういうオシロスコープで、面白いのがリサージュ図形なのですが、これも理系以外の人にはあまりお馴染でありません。
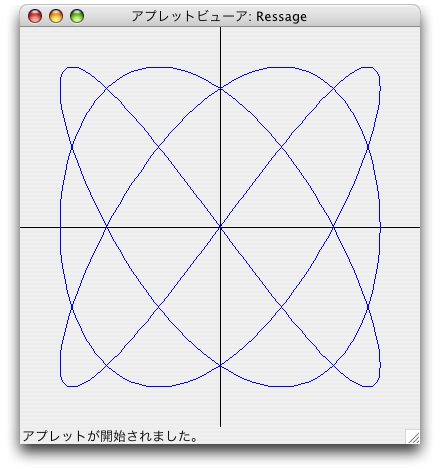
この図形は、円を描くときの三角関数の角度の進み具合を変えてやればすぐ描けます。 円のときは、cosもsinでも0から360度まで行儀良く変化させていきましたが、 cosで0から720度まで変えてしまったらどうなるでしょう? cosだけ2回転もさせちゃったら、まずい気もしてきますが、やってみます。
x = (int) (Math.cos( radian*2 ) * radius + centerx); // 2倍
たとえば、上のようにx座標を求める式で、cos関数の角度を2倍するだけで、変な図形が出てきます。 これをリサージュ図形と呼びます。 これ繰返しを使って何倍にもできるようにしちゃえ!って感じで次のアプレットを作ってみました。 インスタンス変数zoomに倍率をいれておき、どんどん倍率が+1されていくのが特徴です。 2倍から5倍まで変わります。倍率が変わるたびに、色を変えるようにしました。
public void paint( Graphics g ) {
int x, y, lastx, lasty;
int centerx = getWidth( ) /2 , centery = getHeight( ) / 2;
int radius = (centerx > centery) ? centery * 3/4 : centerx * 3/4;
// 座標軸の描画
g.drawLine( 0, centery, getWidth( ), centery );
g.drawLine( centerx, 0, centerx, getHeight( ) );
// 倍率を変えての繰返し
for ( int zoom =2; zoom <= 5; zoom ++ ) {
g.setColor( (zoom == 2 ) ? Color.blue : ( zoom == 3 ) ? Color.red :
( zoom == 4 ) ? Color.orange : Color.green );
lastx = radius+centerx;
lasty = centery;
for (int i=0; i<=360; i++ ) {
double radian = Math.toRadians( i );
x = (int) (Math.cos( radian*zoom ) * radius + centerx );
y = (int) (- Math.sin( radian ) * radius + centery );
g.drawLine( lastx, lasty, x, y );
lastx = x;
lasty = y;
}
}
}
螺旋は、円と似ているのですが、円の半径が角度が変化していくについて変化していきます。 この変化について、一定の割合で変化していくものと、指数的に変化していくものがあり、 ここではその2つについて簡単に描画してみることにしましょう。
蚊取り線香ような螺旋は、アルキメデスの螺旋と呼ばれています。 角度θと半径rの割合が一定の定数cになるような螺旋です。c = r / θとおきますと、各座標は、次のような形になります。
x = c *θ * Math.cos( θ ) + centerx; y = c * θ * Math.sin( θ ) + centery;
この螺旋をアプレットで描画してみましょう。 最大半径を200としまして、360度で最大半径の大きさになるようにcの値を設定します。 paintメソッドの部分だけを記述してあります。 cを求めるのに、一番大きな角度である360を半径で割っておき、それに角度を掛けるようにしてあります。
public void paint( Graphics g ) {
int centerx = getWidth( )/2, centery = getHeight( )/2;
int rotation = 3; // 3 は回転数
int maxradius = 200; // 最大半径
double c = maxradius / (360.0 * rotation);
int lastx= centerx, lasty = centery; // 中心から外へ
for (int i=0; i<=360 * rotation; i++ ) {
double radian = Math.toRadians( i );
int x = (int) (Math.cos( radian ) * c * i + centerx);
int y = (int) (- Math.sin( radian ) * c * i + centery);
g.drawLine( lastx, lasty, x, y );
lastx = x; lasty = y;
}
}
角度と半径が指数の関係にある螺旋で、対数螺旋と呼ばれます。 巻き貝の螺旋がこのような螺旋の構造になっています。r = acθとおきますと、各座標は次のようになります。
x = a * cθ * Math.cos( θ ) + centerx; y = a * cθ * Math.sin( θ ) + centery;
このアプレットでは、6回転ぐらいさせてみましょう。 上の式から考えると、a = e(自然対数)とおくと対数を使って、c = log( r )/ θとなります。 ここで、rは最大半径とします。 paintメソッドだけ記述しますと、以下のようになります。 なお、θは、ラジアン体系を使っています。
public void paint( Graphics g ) {
int centerx = getWidth( )/2, centery = getHeight( )/2;
int lastx= centerx, lasty= centery;
int maxradius = 200;
int rotation = 6;
double c = Math.log( maxradius ) / ( rotation * 2 * Math.PI );
for (int i=0; i<=360 * rotation; i++ ) {
double radian = Math.toRadians( i );
int x = (int) (Math.cos( radian ) * Math.exp( c * radian ) ) + centerx;
int y = -(int) (Math.sin( radian ) * Math.exp( c * radian ) ) + centery;
g.drawLine( lastx, lasty, x, y );
lastx = x; lasty = y;
}
}

リチュースと呼ばれる、代数螺旋は何回転もさせると以下のような美しい螺旋を描きます。 r2 = a2 / θです。 これを描くアプレットを作成しなさい。クラス名は、Lituus(巻杖のラテン語)で。 リチュースは、無限のかなたから、中心に向かって描いていきます。 θを0度から始めてしまうと、いきなり実行時エラーになりますので、0に近い小数から始めるようにします。
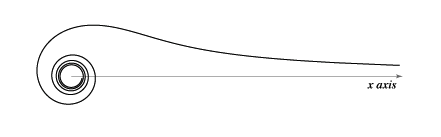
双曲螺旋(hyperbolic spiral)は、c = rθの関係があり、x = (c / θ) * cos θで、y = (c / θ) * sin θになります。 これを何回転もさせるようなアプレットを作りなさい。クラス名は、HyperbolicSpiralで。
| <<Previous Lecture | Next Lecture>> |