第2部 実践編
第2部実践編の内容
実践編では、スポーツ科学を題材にして観察データや計測データを使ったデータ分析の基本手法を学ぶ。もちろんここでとりあげる解析方法のみがスポーツ科学で必要とされるものではないし、不十分であるがもっとも基本的であると思われることをとりあげてみた。さらに専門的な分析方法については第3部上級編でとりあげる。
準備
Spell Off
In[1]:=
![]()
In[2]:=
![]()
データ読み込み/書き込みディレクトリの準備
In[3]:=
![]()
Out[3]=
![]()
In[4]:=
![]()
Out[4]=
![]()
基本記述統計量
記述統計量
慶應義塾大学湘南藤沢キャンパス学生の体力測定
最初に学ぶであろう基本的な統計処理をMathematicaで行うことが本章のテーマである。対象とするデータはスポーツ科学らしく体力測定データとした。その体力測定データは筆者のいる慶應義塾大学湘南藤沢キャンパス(Keio SFC)学生の計測値である。SFC学生の体力測定データを統計処理してみることがどんなことがみえてくるだろうか?
測定項目
ヒトの体力を総合的に表すには次の6項目に分けて体力を考え、それぞれの項目に関するテストを行ってその結果で評価する。筋力、瞬発力、持久力(全身持久力と筋持久力とに分ける事もある)、平衡性、敏捷性、柔軟性がここで取り扱うデータである。
筋力
筋力の評価には握力と背筋力を用いる。握力はもちろん手を握るときの力を測るのだが、大雑把にみて上肢の筋力を測っているものと考えられる。なぜなら、手を握るのに使われる筋肉は前腕の筋肉だからである。これに対して背筋力は背筋、すなわち体幹の筋力を測っていると言える。背筋は人間の身体のなかで最も長い筋肉でもあり、全身の筋力を代表すると言っても過言ではない。
瞬発力
瞬発力とは、短時間にどれだけ大きな力を発揮できるのかを知るための指標となる。筋力が優れていて大きな力を発揮できても、ゆっくりとしか力を出せない場合には瞬発力に優れているとはいえない。従って一瞬にして重たいバーベルを持ち上げないといけない重量挙げ選手達は優れた瞬発力をもつ。
持久力
持久力はどれだけ長い時間運動を持続できるのか?あるいはどれだけの強度で長時間運動を持続することが出来るのかを示す指標である。大雑把には持久力だが、実際には筋持久力と全身持久力とに分けるが、SFCでは全身持久力の指標である最大酸素摂取量を評価値としている。
敏捷性
敏捷性とは、すばしっこさとでも言おうか。バスケットボールで相手をすり抜けてドリブルをするといった場合にはこの敏捷性がより高いほうが有利といえる。単位時間内にどれだけ速く、数多く反復運動を行えるかで評価する。多くの場合、反復横跳び(Side Step)を行って評価する。
柔軟性
柔軟性とは身体の柔らかさである。身体といっても具体的には関節の柔らかさであるといえる。評価には立位体前屈が長年用いられてきたが、立位体前屈の場合には手の長さによって個人差が出てしまうため、最近では長座位体前屈が用いられることが多い。SFCでは長座位体前屈を用いることにしている。
体力測定データを読み込む
![]()
![]()
SFC学生の体力測定データを読み込もう。データの名称は、"SFC2004.txt"である。データは下記のように並んでいる。図はエクセルで見たところ。

{性別(1=男性、2=女性)、年齢(歳)、身長[cm]、体重[Kg]、体脂肪率[%]、右握力[Kg重]、左握力[Kg重]、背筋力[Kg重]、垂直跳び[cm]、反復横跳び[回/20sec]、全身持久力(最大酸素摂取量)[l/min]、長座位体前屈[cm]}
![]()
SFC2004という名前でカーネル上にデータが読み込まれた。ちなみにあらかじめ明らかにおかしいデータ(身長や体重が0である、握力が0である、etc.)は取り除いてある。本来はこのような不正データや欠落データの処理についても行う必要があるが、説明がケース・バイ・ケースになりがちなのでここでは割愛させてもらうことにする。
標本分布
標本
母集団と標本
統計では一般的に大きな集団の傾向をつかむために、しばしば全データの一部分を使って調べることがある。全データのことを「母集団]:population」と呼ぶ。それに対して母集団の一部を「標本:sample」と呼ぶ。全体の傾向をつかむためにその一部を用いるというわけである。それでは今読み込んだSFC体力測定データの「標本数」はいくつだろうか?リストの長さを調べるには、Length[]を使う。
![]()
![]()
741名分のデータをすべてみるのは大変だ。そこで短縮表示で見てみよう。データはリストのリストになっている。入れ子になっているリストの中には1名分の体力測定データ12項目が含まれている。
![]()
![]()
さて、SFC新入生741名のデータをここでは、SFC学生という母集団の傾向をつかむための標本と位置付けてみることにしよう。標本がどのような分布を示しているのかを眺めることは小学校のときにやっただろう。そう、棒グラフで描く度数分布表である。
度数分布グラフを描く関数は、Histgram[]である。
![]()
身長の度数分布
では各測定項目の度数分布グラフを作ってみよう。SFC2004というデータは先ほど説明したように、リストのリストである。内包されているリストには、1名の学生の測定項目が順番に並んでいる。つまり、
{{1人目の性別(1=男性、2=女性)、1人目の年齢(歳)、1人目の身長[cm]、1人目の体重[Kg]、1人目の体脂肪率[%]、1人目の右握力[Kg重]、1人目の左握力[Kg重]、1人目の背筋力[Kg重]、1人目の垂直跳び[cm]、1人目の反復横跳び[回/20sec]、1人目の全身持久力(最大酸素摂取量)[l/min]、1人目の長座位体前屈[cm]},
{2人目の性別(1=男性、2=女性)、2人目の年齢(歳)、2人目の身長[cm]、2人目の体重[Kg]、2人目の体脂肪率[%]、2人目の右握力[Kg重]、2人目の左握力[Kg重]、2人目の背筋力[Kg重]、2人目の垂直跳び[cm]、2人目の反復横跳び[回/20sec]、2人目の全身持久力(最大酸素摂取量)[l/min]、2人目の長座位体前屈[cm]},.....}}
である。度数分布を作るためには、同じ計測項目を取り出してまとめておかなくてはならない。つまり、次のようなデータが必要であるということだ。
{{1人目の身長,2人目の身長,3人目の身長,......166人目の身長},{1人目の体重,2人目の体重,3人目の体重,......166人目の体重},.....}
リストのリスト(2重リスト)が行列だと考えると、これは行列の転置(Transpose)をとることで容易に得られる。前回の行列の説明でも出てきたが、Transpose[]を用いる。ではSFC体力測定データの転置行列を作り出し、そこから身長だけを取り出してみよう。
![]()
[[3]]と後ろにつけたのは、元データの3番目が身長だから転置した場合には、得られたリストのリストの3つ目の要素が身長に相当しているからである。では身長度数分布をグラフにしてみよう。
![]()
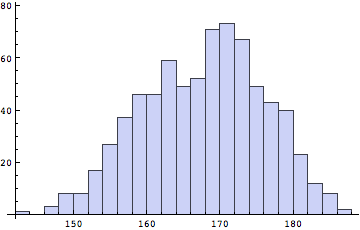
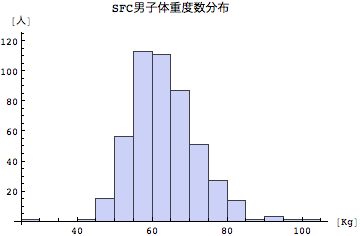
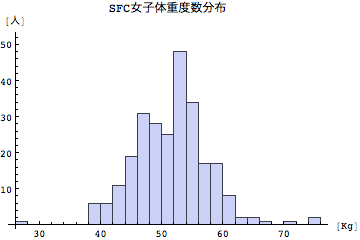
162.5cm以上165cm未満のところに一つ、ピークがあって、さらに172.5cm以上175cm未満の所にもピークがあるように見受けられる。これは男女すべてまとめて表示したからだ。18歳男子高校生の平均身長が、約172cmであるということから、2つめのピークは男子の平均に近い人たちの群を示しているといえよう。これとは異なり、1つめのピークは女子の人数と男子の人数が重なり合って数が多いように見えているだけとも受け取れる。そこで男子だけ、女子だけと性別ごとの度数分布グラフを作ってみよう。では、男子だけ、女子だけ取り出すにはどうしたらよいだろうか?男子は性別の項が1、女子は性別の項が2である。これはちょっと難しいかもしれない。考え込むといくつものプログラムが挙げられるが、男子と女子の性別を示すデータが、1か2であったことを思い出すと、性別つまりデータの1列目の値が1の場合は男、それ以外の場合には女として該当するデータを抜き出してくることが可能である。
![]()
![]()
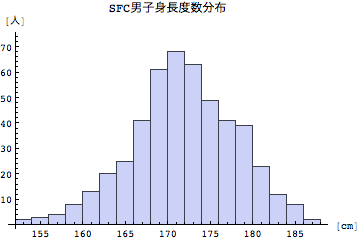
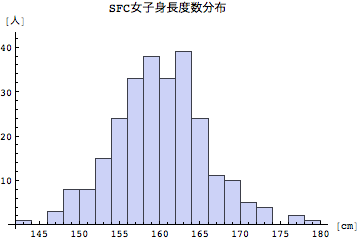
どうやら女子の身長でもっとも度数が多いのは、160cmから162.5cmの群であることがわかる。または、その一つ下の157.5cm以上160cm未満の群かもしれない。
平均・分散・標準偏差
平均
平均とは
すでに基本編でも登場したが、ある母集団の傾向を知るためにもっとも多く使われるのが「平均」であろう。平均とは変量としての数値、![]() ,
,![]() ,...
,...![]() があるときに以下の式によって求められる。
があるときに以下の式によって求められる。
![]()
体力測定データの平均値を求めよう。もう一度、平均や分散を求める手順はやったのでその流れは分かっていることと思う。第3回資料にその計算の方法が記載されているのでそれを参考にしてもらいたい。第3回の授業では自前で平均や分散、標準偏差を計算する関数を作成した。
そんな基本関数ないのか?と思った人もいるだろう。ちゃんと用意されている。
身長・体重の平均値
それでは、早速関数Mean[]を使って身長と体重の平均値を求めてみよう。まずは男子、女子それぞれの身長体重を抜き出そう。次にそれぞれの性別ごとの平均値を求めよう。すでに男女それぞれの身長については取り出してある。同じ方法で体重も取り出してみよう。
![]()
![]()
![]()
![]()
![]()
度数分布グラフから直感的にわかったことと比較してどうだろうか?体重は度数分布グラフを作っていなかったので、ここで確認してみよう。
![]()
度数分布グラフも捨てたもんじゃない。体重の度数分布をみて気が付くのは、SFC新入生の男子の体重は平均より上(つまり重い方)に裾野が伸びているのに対して、女子は平均を中心にして両方に向かって裾野が広がっているように見える。SFC新入生は男子が太りぎみ傾向にあるのではないだろうか?学生の皆さんはどう思うだろうか?またどうも体重に関しては不正データ(あまりにも体重が軽すぎるようなデータ)があるようだ。
不偏分散と標準偏差
不偏分散とは
先ほど体重の度数分布グラフを眺めたときに、男子のデータの分布は平均よりも上側に裾野が広がっているのかということを述べたが、このデータの広がり具合を示すものが分散である。すでに分散についても説明は行ったが、今一度思い出してみよう。繰り返しの説明になるが仮に同じ平均値をもつ母集団があったとしても分散が異なると下の図のようにまったく傾向の違う集団と結論づけられる。
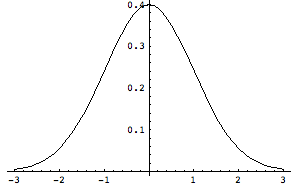
平均0、分散1(標準偏差1)の分布
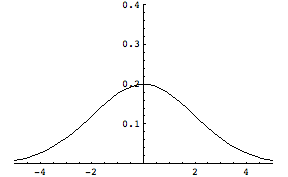
平均0、分散4(標準偏差2)の分布
分散は、すべてのサンプルの平均からの差を二乗することで得られる。
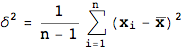
そしてこの分散はVariance[]という関数で提供される
![]()
![]()
![]()
![]()
標準偏差
分散の正の平方根のことを標準偏差と呼ぶ。平方根であるので次元は元データと等しくなるので、どの程度データの広がりがあるのかをつかむにはむしろ標準偏差のほうがわかりやすいときもある。標準偏差はMathematicaでは、StandardDeviation[]という関数で提供される。
![]()
![]()
![]()
![]()
SFC新入生男子学生の身長は、(平均値,標準偏差)=(171.5,6.15)の特徴をもつといえる。分散と標準偏差はともに母集団の傾向を示す変数の一つである。
分布を表す諸変量
その他の特徴量:中央値、歪度、尖度
中央値(Median)
集団の特徴量を示すにはほかにもいくつかの指標がある。中央値(median)は、データの真中にある値のことで平均すると母集団には偏りがある場合などに有効な指標となることがある。
![]()
![]()
![]()
![]()
歪度(Skewness)
度数分布を見たときに、裾野が右側に伸びている、左側に伸びている、と記述したが集団のデータが平均からどちら側に分布しているのかを示すのが歪度である。歪度は以下の式で求めることが出来る
![]()
n= 標本数
δ=標準偏差
3乗が出てくるということは、歪度はデータが平均からみて大きな方(右側)に偏っているときは正の値をもち平均よりも小さい値側に偏っているときには負の値をとることが分かる。
![]()
![]()
![]()
ヒストグラムからは女子の分布はすそ野が左に伸びているように見えたが実際には少しだけ右側(平均より上)に伸びていることが分かった。
尖度(Kurtosis)
尖度は度数分布表でみたときに分布がどれだけ尖っているか?と示す量のことである。
![]()
尖度が小さいとなだらかな分布を示し、大きいと尖っている分布になる。正規分布をするときは尖度は約3を示す、ということも覚えておくとよいだろう。
![]()
![]()
![]()
女子の体重の方が少しだけ平均値に偏り尖った分布だということがわかる
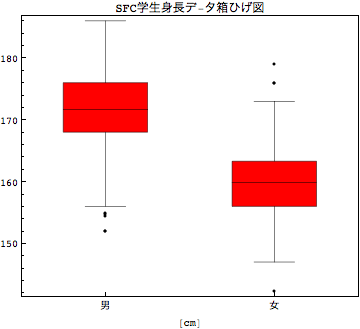
箱ひげ図
特徴量を記述的に表示することが出来たが、もっと直感的に訴えるグラフとして、箱ひげ図というものがある。箱ひげ図は、BoxWhiskerPlot[]という関数で実装されているが、データの中央値を真ん中に描きその上下を第1四分位点と第3四分位点を囲むボックスで描かれる。さらにこれから大きく外れる外れ値を描くかどうかのオプションなどがある。
![]()
検定 (体力測定データを使った平均値の検定)
基本的考え方
ここで,SFC学生が日本人平均値とくらべて体格や体力が優れているのか?それとも劣っているのかということを検討してみたい。これは統計的検定のひとつの方法である。統計的検定にはいくつもの手法があるが、ここでは平均値についての検定を行うこととする。その前に、統計的検定の基本的な考え方を説明しておきたい。
ある事象が確からしいことを確信するに至るには、何らかの定量的な支持を得たい、というのが検定の目的といえる。たとえば、ある集団(ここではSFCの学生集団ということになるが)から何らかの変量を観測・計測したとしよう。そのデータが別の集団のデータと比較して違いがあるかどうかを確かめたいとする。このとき、
(1)全く事前に知識がなく、2つの集団のデータのどちらが大きい・小さい、といったことがわかっていない場合。つまり違いがあるかどうか、を知りたい場合。
(2)事前に何らかの情報をもっていて、2つの集団のうちどちらか一方のデータが大きい(または小さい)ということを予測した上で比較をする場合
の2つのケースが考えられる。どちらの場合においても比較して「差がある」ことを実証したいことには変わりはない。そこで何らかの違いがある、という仮説をたてて検定に臨むわけである。
帰無仮説と対立仮説
帰無仮説 (null hypothesis)と対立仮説(alternative hypothesis)
このとき,「差がある」ということを直接証明するのではなく、「差がない」という逆の仮説が「成り立たない」ことを証明し、「差がある」ということを確信する。というのが一般的統計的な検定の流れとなる。
この「差がない」という仮説のことを、帰無仮説(null hypothesis)とよび、実際に証明したい仮説のことを対立仮説(alternative hypothesis)とよぶ。差がない、という仮説は結局成り立たない(これを棄却されるという)ということが証明されるために、「無に帰する」から帰無仮説と呼ばれる、と覚えておくとよいだろう。
そこで、まずは自分が証明したい事象を仮説(=対立仮説)としてたてる。次にそれを真っ向から否定する仮説(=帰無仮説)をたてる。そしてこの帰無仮説を使って検定を行う。慣習的に帰無仮説は![]() 、対立仮説は
、対立仮説は![]() (or
(or ![]() )と表記される。
)と表記される。
両側検定(two-sided test, )と片側検定 (one-sided test)
ここで検定には,両側検定(two-sided test)と片側検定(one-sided test)の2種類がある。SFC学生の身長が全国の学生と比較して、「高い」か「低い」か分からないが違いがある、ということを知りたいときには結果として得られるものとして、
(1)SFC学生の平均身長は全国平均よりも「高い」
(2)SFC学生の平均身長は全国平均よりも「低い」
(3)SFC学生の平均身長は全国平均と「同じ」
の3つがある。全国の同年齢平均身長(母平均)とSFCの平均身長(標本平均)とをそれぞれ平均値を、![]() とおき、先ほどの帰無仮説と対立仮説に置き換えると両側検定の場合、
とおき、先ほどの帰無仮説と対立仮説に置き換えると両側検定の場合、![]() ,
, ![]() =0
=0![]() ,
, ![]() ≠0
≠0
となる。片側検定の場合にはたとえばSFC生の平均身長が全国平均値よりも高い(はず)、ということを考えるときには![]()
![]()
となる。
帰無仮説の棄却
設定した仮説が真であるとみなして、理論的な可能性と比較して著しく異なる場合、この仮説が正しくない(偽である)としてその仮説を棄却する。仮説を棄却するかどうかということを行うこと、これを検定と呼ぶ。ここでどのようにして帰無仮説を棄却するのかだが、これには正規分布をみて説明をしたい。正規分布のグラフは何を表しているかというと、ある事象が起こりうる、「確率密度関数」である。
平均値が0,分散が1の標準正規分布をつくる
ndist = NormalDistribution[0, 1]
この分布に関する確率密度関数を示す関数を求める.
pdf = PDF[ndist, x]
![]()
Plot[pdf,{x, -3, 3}]
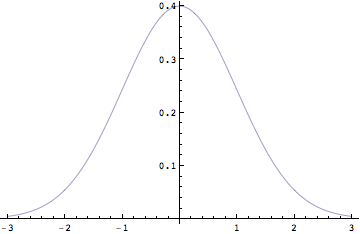
標準正規分布のグラフの横軸は,標準得点(z得点)である。そして縦軸は事象の確率密度である。確率密度というのがなかなか説明しづらいが、釣鐘型の上のグラフの横軸よりも上の面積を全部足し合わせると、1になることをまず覚えておいてほしい。すなわち全ての事象の起こりうる確率を全て足し合わせると1になる、というわけである。そこで横軸のある標準得点位置から、別の標準得点位置までの面積を足すと、目的とする事象の起こりうる確率を知ることが出来る。
標準得点 (z - score)
ところで標準得点とはなんだろうか?身長や体重,あるいは試験の成績など統計的検定を行う対象は、異なる大きさやちらばり(分散)をもっている。そこで様々な大きさや単位をもつ定量的なデータについてはデータを標準化して比較検討を行うことにする。これを標準得点とよぶ。標準得点は、(各測定値\:ff0d平均値)/標準偏差 で表される。
![]()
平均値に関する検定
日本人平均値との比較
それでは、SFC学生の体格・体力が日本人全国平均と比較して違いがあるのか、否かを検定してみることにしよう。そもそも慶應義塾大学SFCの学生が日本人平均値と比べて、体格的、体力的にに優れているのか、劣っているのか、事前知識があるわけではない。つまり、ここでは両側検定を行うことになる。また検定において用いる統計量は体格を示す身長や体重、体力を示す握力や垂直跳びの値の「平均値」である。
統計的検定のパッケージ読み込み
Mathematicaで、統計的検定を行うにはパッケージ HypothesisTestingを読み込む
![]()
母集団の平均値および分散が分かっている場合 (z検定)
母集団の平均値と分散がすでに分かっている場合には、以下の手順をとる。
(1)帰無仮説をたてる。
この場合、H0 = SFC学生の平均値と同年代全国平均値には差がない、となる
(2)有意水準、αを決める。α = 0.05 ( or α = 0.01)。このときのαの値に対応する標準得点(z score)を求めておく。両側検定においてα=0.05の場合のz得点は、![]() (α=0.05) = 1.96であり、
(α=0.05) = 1.96であり、![]() (α=0.01) = 2.58である。
(α=0.01) = 2.58である。
(3)標本のz得点を次の式によって求める
z=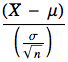

(4)得られたz得点が、|z| > ![]() であれば、帰無仮説を棄却し、有意差があると判断する。|z| <
であれば、帰無仮説を棄却し、有意差があると判断する。|z| < ![]() であれば有意差なしと判断する。
であれば有意差なしと判断する。
全国平均値の確認
ここで検定に必要な、全国平均値を確認しておこう。20歳の全国平均値は以下のようになっている
| 性別 | 身長平均(cm) | 身長標準偏差(cm) | 体重平均(Kg) | 体重標準偏差(Kg) |
| 男子 | 171.00 | 5.41 | 63.10 | 7.52 |
| 女子 | 158.00 | 4.86 | 51.10 | 5.46 |
MeanTestを使う
平均値の検定,MeanTest[ ]
では具体的にMathematica関数を用いて平均値の検定を行ってみよう。平均値に関する検定を行うには関数MeanTest[]を用いる
![]()
基本的な使い方は上のようになっているが,実際には両側検定を行うか否か?母分散(母標準偏差)が既知かどうか、といったオプションを指定する必要がある。
そこで分かっている全国平均値と標準偏差を用いて両側検定を行う手順は次のようになる。
![]()

Reject null hypothesis at significance level"→0.05
α= 0.05 、すなわち5%の有意水準で帰無仮説が棄却されている。すなわち標本平均と母平均は等しい、という帰無仮説が棄却されたわけだから標本平均と母平均は異なる、ということになる。すなわち、男子SFC平均身長は、20歳の男子全国平均値と比較すると5%の有意水準において異なる、といえるわけである。
![]()

α=0.01 、すなわち1%の有意水準ではどうかというと、帰無仮説の棄却が「失敗」している。つまり帰無仮説が正しい、すなわちSFC平均身長と20歳の男子平均身長は1%の有意水準では差がない、ということである。平均値をみてわかるように若干全国平均よりも身長が大きい、といえるがこの違い、それは5%の有意水準では有意差が認められるが、1%の有意水準では有意差はない、ということになる。
次に、女子の平均身長を20歳の日本全国の女子平均身長と比較してみよう。
![]()

![]()

女子の場合には、5%, 1%のどちらの有意水準(危険率)においても有意差があるということになった。つまりSFC女子平均身長は全国20歳女子平均身長と異なる、ということがいえるのである。
母集団の平均値が分かっていて,分散が不明の場合(t検定)
母集団の平均値が分かっているが,その分散が分からない場合には、標本分散![]() を頼りにして母分散
を頼りにして母分散![]() を推定する。
を推定する。
![]()
![]() : 標本平均
: 標本平均
μ : 母平均(母集団の平均)
S : 標本分散の平方根(標準偏差)
n : 標本数
このときには、特にKnowStandardDeviation->XX, KnownVariance->XX,などと指定をしなければよい。
仮に母集団である日本人平均値のみが分かっていてその分散が不明のときに先に行ったことと同じような平均値の検定を行うと以下のようになる。
![]()

先ほどと同じように帰無仮説は棄却されたので5%の有意水準で身長には差がある、と結論付けられる。しかしよくみると先ほどと異なる出力がされていることに気がつくあろう。先ほどは、DistributionはNormalDistribution (正規分布)となっていたが、今度のはStudentTSistribution[481]となっている。481というのは、SFC男子身長データの(個数\:ff0d1)と一致する。
![]()
![]()
練習問題
問:体重に関して,SFC平均値と20歳全国平均値との比較を行い,5%有意水準での検定を行え.
問:以下の体力測定項目の各項目ごとに、それが全国平均値と比較して異なるかどうかを検定せよ。なお、各項目の全国平均値に関しては次の表を参考にせよ。ただし、以下の平均値は20歳の全国平均値を示している。
その結果をもとにして、SFC学生の体力の傾向はどのようなものであるのかを推察せよ。
*元データのうち長座位体前屈に関しては除いている。
| 体力カテゴリ | 項目 | 男子平均 | 男子標準偏差 | 女子平均 | 女子標準偏差 |
| 筋力 | 握力(Kg) | 49.3 | 7 | 30.0 | 5.0 |
| 筋力 | 背筋力(Kg) | 144.6 | 25.0 | 88.5 | 18.4 |
| 瞬発力 | 垂直跳び(cm) | 61.2 | 8.3 | 41.9 | 6.5 |
| 敏捷性 | サイドステップ(回) | 46.3 | 5.4 | 39.7 | 4.9 |
| 持久力 | 最大酸素摂取量(l/min) | 3.0 | 0.44 | 1.93 | 0.32 |
問:体力の特徴を総合的に示すにはこれまでみてきた測定項目をそれぞれ、
筋力:握力、背筋力
瞬発力:垂直跳び
敏捷性:反復横跳び
柔軟性:体前屈
持久力:最大酸素摂取量
などに対応付けて、これらを総合的に本人に提示することが必要とされる。このような問題の場合には、レーダーチャートが便利だといわれている。参考資料にはレーダーチャートを描くプログラムを載せている。このプログラムを利用して、ユーザーから任意の計測データを受け取ったら、その測定項目のレーダーチャートとを出力する関数、EvaluateYourFitness[]を作れ。また実際にデータを入力して確認せよ。その際には10段階のうちSFC平均値を5として考えることにせよ。すなわち、EvaluateYourFitnessを実行すると個人の体力をSFC生の平均値と比較してレーダーチャートで比較する関数を作る、ということである。
*とんでもなく変な値が入力されたときにはどうするか?
参考資料(MathematicaでRaderChart)
RaderChart(レーダーチャート)とは
RaderChartはいくつかの変量を同じ尺度(例えば,0から10まで)にスケール変換した値を見やすく表示したグラフのことである.残念ながらMathematicaには,RaderChartを描く関数はない.そこで次の関数,RaderChart[]は,いくつでも項目を入力してもレーダーチャートが描けるようになっている。こうやって組み込み関数ではない関数もグラフィックス原始関数を用いることで自作することが可能となる.

Example
![]()
分散分析(一元配置分散分析)
分散分析とは
分散分析は,いくつかのコントロール可能な条件によって得られる実験結果に対して,はたしてどの条件が作用を及ぼしたのか?ということを分析しようとする際に用いられる.
一元配置分散分析
Mathematicaでは,分散分析を行うには,ANOVAというパッケージを読み込む必要がある.
![]()
例題 川本データ
実験データ
ここでは,大東文化大学の川本竜史講師の著書である「SPSSとExcelによる統計力トレーニング」(東京図書)から引用した.
データはサッカー選手の体力測定データである.
![]()
![]()
データを確認してみる
![]()

データのならびは,{被験者番号,ポジション,身長,柔軟性,反応時間}である.
ここで,サッカーのポジションと,選手の身長に関連があるのか?ということを考えてみる.
そこで,ポジションと身長だけを抜き出してみる
![]()
![]()
関数ANOVAを使うと一元配置分散分析が簡単に実現できる.一元配置分散分析では,データは{因子,データ}という並びで与えることが必要である.
![]()

![]()
ANOVA[]で出力されるものは、いわゆる分散分析表である。上記表のP値を参考にすることで、有意差検定を行うことが可能である。
クラスター分析(競泳レース分析データのクラスター分析)
多変量解析の手法のひとつに、クラスター分析がある。クラスター分析は変量の傾向によっていくつかの群(クラスター)に標本を分類する手法である。大きく分けて階層的な方法と、非階層的な方法の2つがあるが、ここではデンドログラムを用いた階層的な方法を紹介する。
競泳レース分析データ
競泳レース分析
筆者は(財)日本水泳連盟の医科学委員として数年前から競泳日本選手権におけるレース分析に関わっている。まだ記憶に新しいアテネ五輪における水泳陣の活躍は水泳研究者として嬉しい限りである。我々レース分析スタッフは日本選手権会場内で選手・コーチに迅速なフィードバックを目指して各選手のレースに関するデータを提供することを行っている。そこでは予選・準決勝のレース情報を翌日の決勝前までにレースペースの詳細情報、すなわち区間通過時間、ストロークタイム(一かきに要する時間)、ストロークレングス(一かきで進む距離)、などを提供している。
選手・コーチらはこれらを見てオーバーペースであったり、ライバルのレースペースから自己の戦略を練り直す、といったことに役立っているものと期待している。
このレース分析データを用いて本節では、選手のレースペースを選手の特性とみなして選手達には一体どの程度のレースパターンが存在するのであろうか?ということをみることにする.レースペースが選手の特性?と首をかしげる人もいるかもしれないが,例えば前半から飛ばして最後はばててしまう選手.前半は抑え気味に泳いで後半スピードを上げる選手,実際こうした傾向は我々水泳競技者なら誰でも知っているし,うまいレース展開が出来た,つまり持っている実力を十分に発揮できた,と思えるときにベストタイムが更新できるものである.そこで,この各人がみせるパフォーマンスとしてのレース展開を題材にしてみようと思う.
変量の定義
ここではこの選手のレースペースは、選手の持つ特徴であると考え、男子200m自由形を対象にして、各50m区間(0から50m、50mから100m、100mから150m、150mから200m)における、ストロークレイト(SR : 1分間に何かきしているか?)、ストロークレングス(SL : 一かきで進む距離)を変量とする。選手が自分の意思によって変化させていると考えられるこのストロークレイト(ピッチと言ってもよい)、ストロークレングスの各局面における組み合わせは、選手の戦略、あるいは選手の能力を示しているのではないかと考えたからである。
従って、
SR = {SR1,SR2,SR3,SR4}
SL = {SL1,SL2,SL3,SL4}
の合計8つの変量を用いる。
競泳レース分析データの確認
![]()
![]()
![]()

![]()
データは、行列形式になっているが、選手IDのほかに、各局面ごとの
![]()
![]()
データの並びは以下のようになっている.
| Year | Sex | Race | Time200 | SV1 | SV2 | SV3 | SV4 | SR1 | SR2 | SR3 | SR4 | SL1 | SL2 | SL3 | SL4 |
| 年度 | 性別 | 予選・準決勝・決勝 | 200m自由形タイム | 泳速度1 | 泳速度2 | 泳速度3 | 泳速度4 | ストロ-ク頻度1 | ストロ-ク頻度2 | ストロ-ク頻度3 | ストロ-ク頻度4 | ストロ-ク長1 | ストロ-ク長2 | ストロ-ク長3 | ストロ-ク長4 |
男子,女子ごとにデータをわけておく.2003年度のデータを抽出し,男女別に変数にしまっておく.
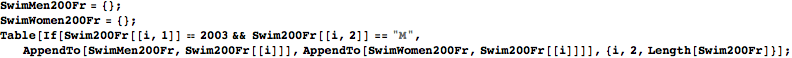
クラスター分析
変量の確認
さてクラスター分析の進め方であるが,ここで取り扱っている競泳200m自由形のレースデータについて触れておく.競泳のレース分析で得られるデータは,以下の2つからなる.
(1)ストローク頻度, Stroke Rate: SR (cycle/min)
(2)ストローク長, Stroke Lnegth : SL (m/cycle)
ここから泳速度, Swimming Velocity : SV (m/s)は以下の式で表される.
SV (m/s) = 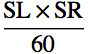
このSV, SR, SLが,4つの局面ごとに記録されているものがここで取り扱っている競泳レース分析データである.第1局面(0mから50m),第2局面(50mから100m),第3局面(100mから150m),第4局面(150mから200m).例えば,男子の1人目のデータで確認すると
![]()
![]()
第1局面のストローク頻度とストローク長を掛け合わせ,1秒間あたりの速度を求めてみると,5列目のデータと一致することが分かるであろう.
![]()
![]()
ここでは,第1局面から第4局面までの4局面間で,選手のパフォーマンスがストローク頻度とストローク長によって表されていて,このパターンが選手の戦略であるという大胆な仮説のもとにクラスター分析を行うことにする.そこで用いる変量は,SR1からSR4とSL1からSL4までの8変量ということになる.
標本をクラスターにわけるには,FindCluster[]を用いる.クラスターに分ける際に標本間距離の算出にはデフォルトではユークリッド距離が用いられる.
クラスター分析の関数 FindCluster
![]()
![]()
![]()
![]()
特にクラスタ判別のための距離関数を指定しないと,2つのクラスターに分けられたことが分かる.
距離関数とは,それぞれの標本が他の要素とどの程度隔たっているのかを規定する関数である.Mathematicaでは特に指定しないかぎり,ユークリッド距離が用いられる.ユークリッド距離とは,![]()
で表される距離のことである.
![]()
デフォルトのクラスター分析結果を見るには,デンドログラムを使うのが普通である.
![]()
![]()
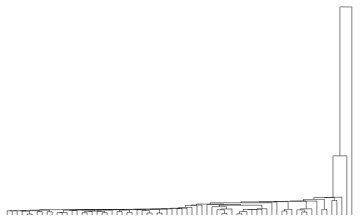
![]()
少々,見難いのでこの場合デンドログラムを横向きに表示してみる.
![]()

変量だけを用いてクラスタ分析すると,実際にその標本がどのようなラベル(例えば,被験者名や試技番号)を持っているのかが分からなくなってしまう.そのため,実際にはラベルをもたせたデータでクラスタ分析を行ったほうが,あとで便利である.
以下では,元データに存在した200m自由形の最終ゴールタイムを持たせた標本をクラスタ分析にかけている.ただし,データの1から8番目までのデータはクラスタ分析自体には関連がないために,解析の際には,1番目から8番目までのデータを抜いて計算を行っている.
![]()
実際には上のFindCluster[ ]を用いるのだが,そのあとのグラフ表示ができないために,以下のDendrogramPlot[ ]を用いてクラスタ分析を行ってその後,樹形図表示(デンドログラム)を行う.
距離関数には,ユークリッド距離.クラスタリングには,最大距離法を用いている.
![]()
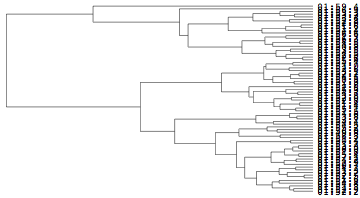
デンドログラムの右に表示しているゴールタイムは小さすぎてよく見えないが,グラフを引き伸ばすとそれは確認できるはずである.
距離関数には,ユークリッド距離.クラスタリングには,Ward法を用いるとやや違った結果が得られる.
![]()
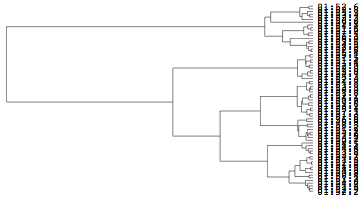
DendrogramPlot[ ]で解析された後に,描かれた上の図は以下のように,階層的クラスタリング(Agglomerate[ ])で求めた結果を,DendrogramPlot[ ]で描画することでも同じことが可能である.この場合には,中間成果物であるcl3(この場合)をみれば,その中に含まれているデータを確認することが出来る.
![]()
![]()
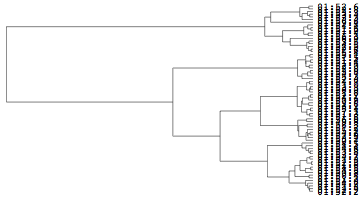
実際,この事例では標本数が多いので,視認しにくい.
クラスタに分割された後で,任意の個数のクラスタにまとめてしまうとより群の違いが見えてくる.
例えば,クラスタを上位7つにすると決めると
![]()
と,7つのクラスタに分割するようなことが可能である.
判別分析
判別分析とは
多変量解析の手法の一つに判別分析(discriminant analysis)というものがある。これは医療診断などの分野ではすでによく知られた手法であるがバイオメカニクスの分野ではあまりなじみがない。例えば臨床検査の結果、いくつもの変量を総合的に判断して、特定の病気であるのか、そうでないのか、それとも病気の予備群であるのかといったようにいくつかの群に分類することに使われている。もちろん、医師の判断がそこには介在するのは言うまでもない。
ここではスポーツデータについて判別分析の適用例を紹介する。
判別分析には大きく分けて、線形判別分析と非線形判別分析がある。非線形判別分析の代表例はマハラノビスの汎距離による判別分析である。マハラノビスの汎距離による判別は、データをその分散によって標準化した上で判別する方法といってもよいだろう。
線形判別分析
線形判別分析の考え方
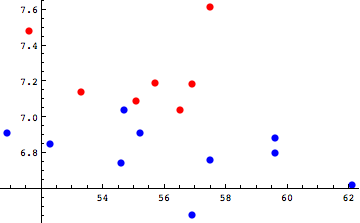
最も簡単な線形判別分析の場合、標本を2つの群に分けるということを考える。2変量{x1,x2}の場合を例に挙げれば、ある2つの群、GroupA、GroupBから得られた標本が図の様に分布する。
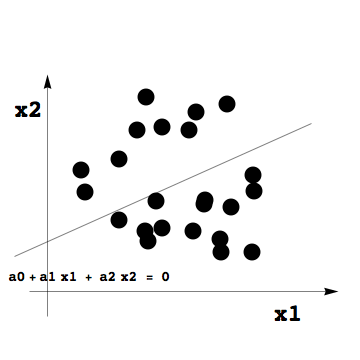
この場合、2群を分ける直線を求めるということは、すなわち判別式
a0 + a1 x1 + a2 x2 ==0
を求めるということに相当する。この直線の上側にデータが存在すれば,その標本はグループAに所属して、直線の下側にデータがあれば,標本はグループBに所属する、とみなすわけである。この直線は、「ちょうどよい具合」に群を分かつ必要があるが、数式の導出に至る過程については統計の専門書に譲ることにする。
線形判別分析のための関数群
変量の平均値 Make Each Row Mean Value
標本の各列データ,すなわち同じ変量の平均値を計算する
In[5]:=
MeanEach[data_]:= Map[Mean[#]&,Transpose[data]]
分散共分散行列 Make Sij Matrix
分散共分散行列を求める
In[6]:=
MakeSMatrix[data1_,data2_]:= Module[{mean1,mean2,smatrix,i,j,k1,k2},
mean1 = MeanEach[data1]; mean2 = MeanEach[data2];
trdata1 = Transpose[data1]; trdata2 = Transpose[data2];
smatrix =
Table[
Table[
(Apply[Plus,
Table[(trdata1[[i,k1]]-mean1[[i]])(trdata1[[j,k1]]-mean1[[j]]),
{k1,1,Length[data1]}]]+
Apply[Plus,
Table[(trdata2[[i,k2]]-mean2[[i]])(trdata2[[j,k2]]-mean2[[j]]),
{k2,1,Length[data2]}]])/(Length[data1]+Length[data2]-2),
{j,1,Length[trdata2]}],
{i,1,Length[trdata1]}];
Return[smatrix];
]
共分散行列を求める関数,Covariance[ ]があるのでそれを用いてもよい.
連立一次方程式を解く Solve Linear Equation for aij
連立一次方程式を解く
In[7]:=
SolveAij[mtrx_,list1_,list2_]:= Module[{exceptA0,a0},
exceptA0 = LinearSolve[mtrx,MeanEach[list1]-MeanEach[list2]];
a0 = -(exceptA0.MeanEach[list1]+exceptA0.MeanEach[list2])/2;
PrependTo[exceptA0,a0]
]
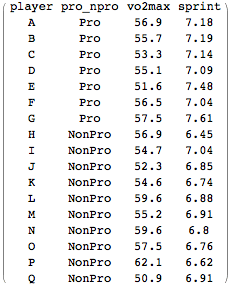
例題:サッカー選手の生理学的特性
標本について
このデータは,筆者の友人である大東文化大学講師,川本竜史氏から提供いただいたものであり,彼の著書でありスポーツ統計学入門書「SPSSとExcelによる「統計力」トレーニング―スポーツデータで分析力を身につける」の事例データでもある.したがって結果を川本氏の書籍と見比べることも可能である.
In[8]:=
![]()
Out[8]=
![]()
In[9]:=
![]()
In[10]:=
![]()
Out[10]//MatrixForm=
In[11]:=
![]()
Out[11]=
![]()
In[12]:=

Out[16]=
In[17]:=
sij=MakeSMatrix[pro,ama]
Out[17]=
![]()
In[18]:=
a = SolveAij[sij,pro,ama]
Out[18]=
![]()
In[19]:=
![]()
Out[19]=
![]()
In[20]:=
![]()
Out[20]=
![]()
ここで結果をながめてみる。判別関数のここでの意味は判別関数に各選手のパラメータX1(VO2), X2(Sprint)を代入して解いた場合、結果が正であれば結果はプロと判断された、ということになる。逆に負となった場合には2つのパラメータによる推定は、選手をノンプロと判別した、ということである。このデータからアマチュア選手の2人目が正の値に判別されているため、この選手がプロ並みの能力をもつ、と判断された、ということになる。
ただし、この使い方には問題があって、通常推定式を作成したデータを再度検証することに使うことはなく、別のデータをもってきて判別式にかける、ということがおこなわれる。
非線形判別分析(マハラノビスの汎距離による判別分析)
非線形判別分析の考え方
アルゴリズム
各群母集団の各変量の平均値を求める
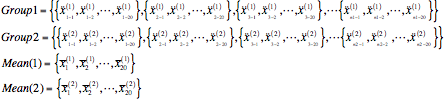
各群母集団の変量の共分散行列を求める
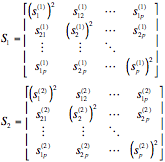
マハラノビスの汎距離Dを求める
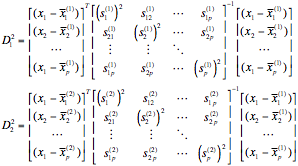
マハラノビスの汎距離が小さいほうの群に属する
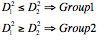
Make CoVariance Matrix
2変量の共分散を求める関数
In[65]:=
MakeCovariance[data1_,data2_]:=
N[(data1.data2 - Length[data1] Mean[data1] Mean[data2])/
(Length[data1]-1)]
Make Variance Covariance Matrix
共分散行列を求める関数。つまり各変量毎に他の変量との共分散をつぎつぎに求めていくだけ
In[66]:=
MakeVarianceMatrix[data_]:=
Block[{i,j},
Table[
Table[
MakeCovariance[Transpose[data][[i]],Transpose[data][[j]]],
{j,1,Length[Transpose[data]]}],
{i,1,Length[Transpose[data]]}]]
マハラノビスの距離
マハラノビスの距離Dは以下のようにして求めることが出来る。
まずは共分散行列や変量の平均値ベクトルを必要としないバージョン。この場合毎回共分散行列を計算し直すので大変な時間がかかる
In[67]:=
MakeMaharanobis[motherdata_,rawdata_]:=
Block[{xlist,eq,dd,replace},
xlist = Array[x,Length[Transpose[motherdata]]];
eq = (xlist-MeanEach[motherdata]).
Inverse[MakeVarianceMatrix[motherdata]].
Transpose[{xlist - MeanEach[motherdata]}];
replace = Table[StringJoin[
ToString[xlist[[i]]],"->",ToString[rawdata[[i]]]],
{i,1,Length[rawdata]}];
dd = Evaluate[eq /. ToExpression[replace]][[1]]
]
次は平均値ベクトル、共分散行列の逆行列を与えるバージョン。引き数の数で見分けられる
In[68]:=
MakeMaharanobis[MeanVector_,InverseVMatrix_,rawdata_]:=
((rawdata-MeanVector).InverseVMatrix.
Transpose[{rawdata-MeanVector}])[[1]]
この距離が近いほうが、所属する群であるといえる
マハラノビスの距離による判別
まずは母集団の平均値ベクトル、共分散行列等の計算も行わなくてもよいバージョン
返り値が1であれば引き数1の群に所属し、-1であれば、引き数2の群に所属する
In[71]:=
DecideWhichMaharanobis[mother1_,mother2_,data_]:=
Block[{d1,d2},
d1 = MakeMaharanobis[mother1,data];
d2 = MakeMaharanobis[mother2,data];
If[d1 <= d2,1,-1]
]
3つの群に判別するバージョン
返り値が1であれば引き数1の群に所属し、-1であれば、引き数2の群に所属する。さらに返り値が0であれば引き数3の群に所属している(少林寺も含む場合用いる)
In[72]:=
DecideWhichMaharanobis[mother1_,mother2_,mother3_,data_]:=
Block[{d1,d2,d3},
d1 = MakeMaharanobis[mother1,data];
d2 = MakeMaharanobis[mother2,data];
d3 = MakeMaharanobis[mother3,data];
If[d1 <= d2 && d1<=d3,1,
If[d2 <= d3, -1, 0]]
]
次は母集団の平均値ベクトル、共分散行列等の計算を行ったうえでマハラノビスの汎距離を求めどちらの群に属するのかを判定する関数
2つの群に判別するバージョン
In[73]:=
DecideWhichMaharanobis[Mean1_,InverseS1_,Mean2_,InverseS2_,data_]:=
Block[{d1,d2},
d1 = MakeMaharanobis[Mean1,InverseS1,data];
d2 = MakeMaharanobis[Mean2,InverseS2,data];
If[d1 <= d2,1,-1]
]
3つの群に判別するバージョン
In[74]:=
DecideWhichMaharanobis[Mean1_,InverseS1_,Mean2_,InverseS2_,
Mean3_,InverseS3_,data_]:=
Block[{d1,d2,d3},
d1 = MakeMaharanobis[Mean1,InverseS1,data];
d2 = MakeMaharanobis[Mean2,InverseS2,data];
d3 = MakeMaharanobis[Mean3,InverseS3,data];
If[d1 <= d2 && d1<=d3,1,
If[d2 <= d3, -1, 0]]
]
例題: 格闘技の打撃技における腕の加速度からの格闘技スタイル判別
格闘技と一言で言っても、国技でもある相撲、柔道、剣道、空手、少林寺拳法と我が国では幅広く、ひとくくりにできない。ここでは打撃技をもつ格闘技の代表として、空手、ボクシング、少林寺拳法の3つを取り上げる。
筆者は15年ほど前に、多くの選手をあつめて彼らの打撃力を計測した経験がある。詳しくは拙著、データサイエンスをご覧頂きたい。
この一連の実験では打撃する腕に加速度センサを装着したが、実験後にわかったことは格闘技種目(ここでは、空手/ボクシング/少林寺拳法)のそれぞれで波形が特徴的であるということである。確かに肉眼では格闘家の打撃フォームが違うのであるから当たり前ではあるが、当時は動きの違いがセンサ信号にも現れるということが、新鮮であった。人間の目視で違いがわかるとすれば数学的に波形の違いを判別できないか?と考えてこの非線形判別分析を適用してみた。
すると期待通り波形から格闘技種目の判別ができることがあきらかになった。
参考文献
(1)太田憲,仰木裕嗣,木村広,廣津信義著,データサイエンスシリーズ11,スポーツデータ,共立出版, 2005.8.
(2)仰木裕嗣, 杢野隆直, 山岸正克, 宮地力:加速度信号を用いた身体運動の分析方法に関 する研究\:ff5e第一報: 格闘技種目の判別および突き技衝撃力の推定, 日本機械学会スポーツ工学1997講演会論文集, pp.155-159, 日本機械学会1997スポーツ工学シンポジウム講演会, 岐阜, 1997.10��
そこで生データを打撃直前の0.2秒間分とってきて、等間隔でそろえて用意する。
In[22]:=
![]()
Out[22]=
![]()
![]()
データは0.2秒間の加速度波形が0.01秒ごとに記録されている
In[82]:=
![]()
Out[82]=
![]()
空手選手の場合45試行分
In[83]:=
![]()
Out[83]=
![]()
ボクシング選手の場合50試行
試しにデータを見てみる
In[92]:=
![]()
Out[92]=
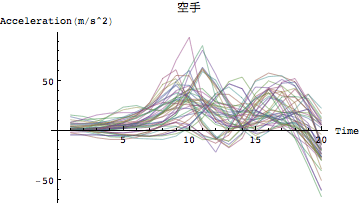
Out[93]=
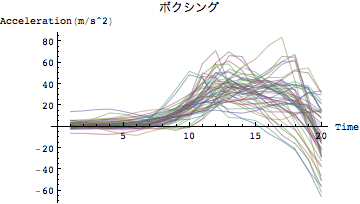
波形に違いがあることを確認できるだろうか?
ここで空手競技者データのなかから1つを抜き出して果たしてそれが、空手競技者の動きであると判別されるか、確認してみよう
ユーザー関数の、DecideWhichMaharanobis[]は、1を返すと最初の群、-1を返すと次の群に変量が分類される。
In[94]:=
![]()
Out[94]=
![]()
空手競技者20番目の実験データは確かに空手競技者の動きであると判別された。
In[95]:=
![]()
Out[95]=
![]()
主成分分析(未完)
主成分分析とは?
主成分分析は多くの変量の値を,出来るだけ少数の変量にしてそのデータの特徴を見出すための手法であるといえる.例えば,大学入試センター試験では数科目の試験を受けることが通常だが,数科目を総合した学力をみているのだといえる.スポーツで言えばバッテリーテスト,あるいはパフォーマンステストと呼ばれるような選手の能力判定テストにおける複数の変量から選手の特性を見出すといったことに使われる.![]() からなる p個の変量をもつデータについて,
からなる p個の変量をもつデータについて,![]()
という線形結合を用いることで総合的な指標を新たに導き出すものである.そして出来るだけ,元データの情報量を失うことなく新しいこの総合的な指標のうち,独立する指標を以下のようにもとめ,これでデータを記述するものである.![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
.......![]() =
= ![]()
![]() , ....,
, ...., ![]() のことを第1主成分,第2主成分,第3主成分,...第m主成分,と呼ぶ.
のことを第1主成分,第2主成分,第3主成分,...第m主成分,と呼ぶ.
パッケージの読み込み
In[127]:=
![]()
例題:2変量の場合での主成分分析の理解
社会統計調査指標データ
ここでは,総務省統計局が発表している2006年度の社会統計調査指標から,日本の各都道府県における教育施設(公民館,図書館,博物館,青少年教育施設など)とスポーツ施設(屋外施設,屋内施設,プールなど)を2つの変量として主成分分析に挑戦してみよう.
まずはデータを読み込む
In[96]:=
![]()
In[97]:=
![]()
Out[97]=

日本語が文字化けしているので,お決まりの手順により訂正しておく.1行目にはデータのプロパティが書き込まれている.
In[98]:=
![]()
Out[98]=
![]()
2行目以降のデータを用いてまずは,変量の関係をみるためにグラフで表示してみる.
In[99]:=
![]()
Out[99]=
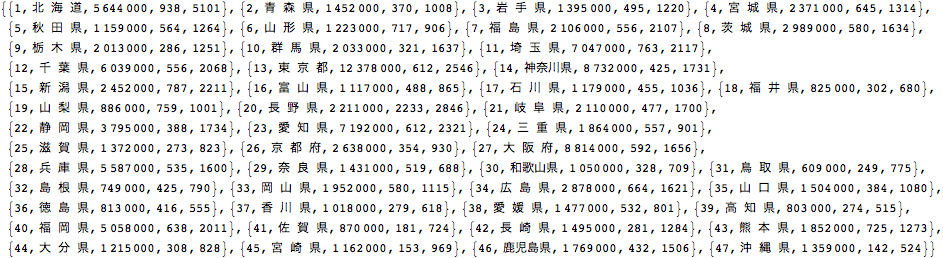
都道府県によって人口は相当異なるので,10万人あたりの施設数に変換し,それを散布図にしてみる
In[102]:=
![]()
Out[103]=
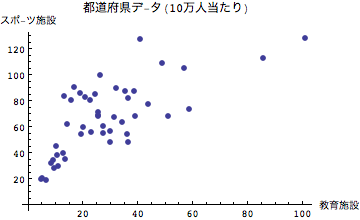
散布図から見えてくることは,教育施設の充実とスポーツ施設の充実振りはどうも右肩上がりの比例関係に近いような傾向がわかる.この分布を1本の直線で表すことを考えることが主成分分析の出発点となる.
2個の変量の場合の考え方
考え方の前提
![]() を使って次のような線形一次結合を考える.
を使って次のような線形一次結合を考える.
z = ![]()
合成変量の分散の最大化,という観点から主成分を求める

In[104]:=
![]()
Out[104]=

それぞれの変量の平均値,分散を求めておく.
In[108]:=
![]()
Out[108]=
![]()
In[109]:=
![]()
Out[109]=
![]()
In[110]:=
![]()
Out[110]=
![]()
In[111]:=
![]()
Out[111]=
![]()
分散共分散行列も求めておく.
In[113]:=
![]()
Out[113]=
![]()
In[114]:=
![]()
Out[114]=
![]()
In[115]:=
![]()
Out[115]=
![]()
In[116]:=
![]()
Out[116]=
![]()
In[117]:=
![]()
Out[117]=
![]()
In[118]:=
![]()
Out[118]=

In[119]:=
![]()
Out[119]=

In[122]:=
![]()
Out[122]=

In[129]:=
![]()
Out[129]=
![]()
情報損失量の最小化,という観点から主成分を求める
一般的な場合(p個の変量の場合)
複数の変量と先ほど述べたが,変量は以下のように得られていると仮定すると,主成分分析ではp個の変量をより少ない変量でその特徴を表すことを考える.
| 変量個体 | ... | |||
| 1 | ... | |||
| 2 | ... | |||
| 3 | ... | |||
| ... | ... | ... | ... | ... |
| n | ... |
最初からたくさんの変量を用いたのでは理解がし難いので,ここではまず2変量の場合を例としてその考え方を学ぶ.
例題:体力測定データからみえてくる体力要素
体力測定データの概要
ここで取り扱うのは,とある集団から得られたサンプルデータ30人分である.体力測定はこの章以外でも取り扱うが,ここでは以下の体力測定要素を
例題:十種競技選手の能力を測る
参考文献
[1] 田中豊,脇本和昌著,多変量統計解析法, 現代数学社, 1983
[2] 小林道正,小林厚子著,Mathematicaによる多変量解析,現代数学社, 1996
最小二乗法(単回帰:力の計測法)
ラケットのひずみから作用した力を求める
筆者の研究分野はスポーツ工学、スポーツバイオメカニクスである。スポーツ工学はスポーツ用具の開発や、新しい計測方法の開発、さらには用具と人間のインターフェースに関連する研究であるといえる。もう一方のスポーツバイオメカニクスとは、スポーツや人間の運動における身体運動の仕組みや働きを分析する研究分野である。本章では、スポーツバイオメカニクス研究では頻繁に行う、力の計測を題材にしていくつかのトピックを学ぶ。具体的にはラケットの歪み(ひずみ)を計測することで衝突時やスイング時にシャフトに作用している力が推定できることを知ろう。「歪み」で「力」を計測するというのが、今回行うことである。そして、今回学ぶ処理の技法は最小二乗法と相関である。
力の計測方法
力と歪み(ひずみ)
ひずみ
物体に力が作用すると、変形が生じることがある。物質の中身の構造までもが変形する(塑性変形)場合は別として、加えた力は変形量に比例することが一般的な現象として観察される。バネがそれである。バネばかりは、ぶら下げたものの重さに比例してその伸びが決まっているため利用される。バネの伸びが重さに比例していなければ誰もバネをはかりとしては用いないだろう。同様に一般に硬くて変形しないだろうと思われるような素材でも力が加えられると微小ではあるが変形することが知られていて、その変形量は加えた力に比例する。そこで加えられた力を知るために、どのくらい歪んだかを知ろうというのが今回のテーマである。
ここで、「ひずみ」は、元の長さ(l)と力が加わって伸びた長さ(+Δl),縮んだ量(-Δl)との比、![]() で表される。1mの棒が力を加えられて1mm伸びたとしよう。するとひずみ量は、
で表される。1mの棒が力を加えられて1mm伸びたとしよう。するとひずみ量は、
ε = ![]()
ひずみゲージ
ひずみゲージとは、ひずみによって応力(加えられた力だと思ってほしい)を計測するための小さなセンサである。実はひずみゲージは精密抵抗のことである。一般にひずみゲージは合金素材が用いられているが、精密に作られた銅線のようなものだと思って欲しい。小学校のときに習ったように、銅線を流れる電流はその銅線のもつ抵抗によって流れを変える。銅線の断面積が大きくなれば電気は流れやすくなるため流れる電流は増加する。逆に銅線が伸びて断面積が小さくなれば抵抗は大きくなり、電流は流れにくくなる。道路にたくさん、人が歩いているときに道が広いほど歩きやすいのと似ている。
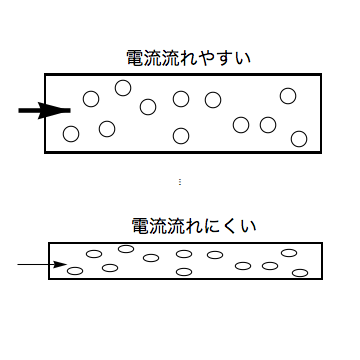
(図:銅線の抵抗変化)
![]()
参考URLには典型的なひずみゲージが載っている。このようなひずみゲージを物体表面に貼り付ける。ひずみゲージ表面と鉛直上方向から力が作用したらどうなるだろうか?下方向にわずかではあるが「たわむ」だろう。そして力がある臨界点を超えなければその変形量は力に比例する。そしてその変形量は同時にひずみゲージの抵抗変化にも比例する。つまりあらかじめ分かっている電圧をかけておくとひずみ量の変化は抵抗の変化によって電流の変化となるわけである。
ところが電流の変化を捉えることは、そう一般的ではない。電圧の変化を捉えるほうが簡単である。どの程度の歪みが生じるかというと、例えば120Ωのひずみゲージに、1×![]() ストレイン(ひずみの単位:元の長さからどの程度伸び縮みしたのかという指標)のひずみが生じた場合、抵抗値は0.24Ω変化する。きわめて微小である。この微小な変化を捉えるために、ここでホイーストンブリッジが登場する。
ストレイン(ひずみの単位:元の長さからどの程度伸び縮みしたのかという指標)のひずみが生じた場合、抵抗値は0.24Ω変化する。きわめて微小である。この微小な変化を捉えるために、ここでホイーストンブリッジが登場する。
ブリッジ回路(ホイーストンブリッジ)
ホーストンブリッジとは次の図のような回路を指す。抵抗素子の抵抗値はすべて同じ大きさであると仮定している。
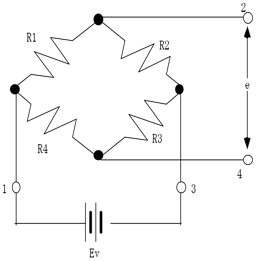
(図:ホイーストンブリッジ)
ここで点1・3間の電圧が一定で、抵抗素子の抵抗が全く等しければ点2・4間に電位差は生じない。つまり![]() 電位差と聞いて「うっ…」と拒否反応が始まりそうな人は、電気の流れではなくて電圧は標高差、抵抗は管の太さ、電流は流れる水量だと思ってみればよい。話を元に戻す。ここで全ての抵抗は同じと書いたが、その一つR1は物体表面に貼り付けてあるひずみゲージだとする。すでに説明したように上から力を加えられて物質が変形を起こした場合、ゲージ素子が伸びることからひずみゲージR1の抵抗は小さくなる。仮にδR(Ω)が変化量だとしよう。するとこのとき
電位差と聞いて「うっ…」と拒否反応が始まりそうな人は、電気の流れではなくて電圧は標高差、抵抗は管の太さ、電流は流れる水量だと思ってみればよい。話を元に戻す。ここで全ての抵抗は同じと書いたが、その一つR1は物体表面に貼り付けてあるひずみゲージだとする。すでに説明したように上から力を加えられて物質が変形を起こした場合、ゲージ素子が伸びることからひずみゲージR1の抵抗は小さくなる。仮にδR(Ω)が変化量だとしよう。するとこのとき![]() オームの法則からR1を流れる電流I1は、以下のように求められる(小学校で習ったかな?)。
オームの法則からR1を流れる電流I1は、以下のように求められる(小学校で習ったかな?)。
![]()
![]()
ここでR1両端の電位E12は
![]()
![]()
同様にして
![]()
![]()
R4両端の電位E14は
![]()
![]()
![]()
![]()
ここで分数が出てきた。Mathematicaは分数もお手のものだ。異なる分母を持つ分数を通分するには、Together[]を用いる。
![]()
![]()
![]()
分子に共通因子Evが見つかったのでもう少し簡略できることが分かる。簡略するには、すでに出てきたがSimplify[]を用いる。
![]()
![]()
![]()
式から、4つの抵抗R1からR4が全て同じ場合には分子が0になるため2―4間の電位差はなく、そこに電流が流れないことが分かる。あるいは、全部が同じ抵抗値ではなくてもR1R3=R2R4を満たせば分子が0になるため、平衡状態が生じて電位差がないために電流が流れないことも明らかである。
ここでなんらかの原因(実際には力を想像して欲しい)で歪みが生じて抵抗値が変わったとする。すると歪みに応じて抵抗値が変化することから、抵抗変化から2―4間に電位差が発生し、結果電圧の変化が観察される。この電圧の変化から加えられた力を推定するというのが道筋である。
力計測の実際
計測装置など
それでは早速、力とひずみの関係を調べてみよう。スポーツにちなんで今回はラケットのシャフトに生じるひずみを計測することによってインパクト時、あるいはスイング時にシャフトに生じている力を推測することにする。計測の手順は以下のとおり
ラケットのシャフトにひずみゲージを貼り付ける

(図:ひずみゲージ貼り付けの図、表と裏に貼り付けてある)
シャフトの表と裏にゲージを貼り付けたということは一方向に曲がった場合に、片方のゲージは伸びてもう片方のゲージは縮むということになる。そこで実際に対象物に貼り付けているゲージは2枚だけということになって、先ほど説明したブリッジ回路のように4つの抵抗素子がないことになる。そこで回路をブリッジにするために補う必要がある。これをやってくれるのが、ブリッジボックス(ブリッジ回路)である。この例の場合、ブリッジボックスは先の表裏に貼ったひずみゲージをR1, R2として、残りのR3,R4の抵抗を肩代わりしてくれる。

(図:ブリッジボックス、ブリッジ回路を構成してくれるボックス)
次にストレインアンプに接続する。すでに述べたようにブリッジ回路にしたとしてもひずみ量の変化は微小であり、抵抗値も微小変化しか示さない。そこで電圧の変化も同様に微小であるためこれを増幅してから計測することが一般的である。この増幅をやってくれるのが「アンプ」である。皆さんもステレオを持っているならば「アンプ」というパーツがあることくらい知っているだろう。アンプは英語のアンプリファイアー(Amplifier)の略、和製英語である。

(図:動ひずみアンプ)
歪→力
ブリッジ回路にしたら、いよいよ計測だ。要は加えられた力とひずみとの関係が知りたいのであるから、あらかじめ分かっている力をラケットのシャフトに作用させ、そのときのひずみ量を調べればいいのだということにすぐに気がつくだろう。当然だが何も力が作用していなければひずみは0のはずである。そして力が大きくなっていけばそれに比例して生じるひずみも大きくなっていくだろう。したがって、異なる力を何回かかけてやることでその傾向がみえてくるのではないだろうか?この過程を図で表すと次のようになる。
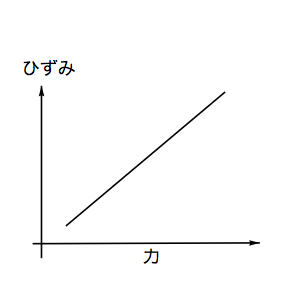
ところでひずみ量は結局のところアンプからの出力では電圧の変化になるため下の図に置き換えてしまってもよい。
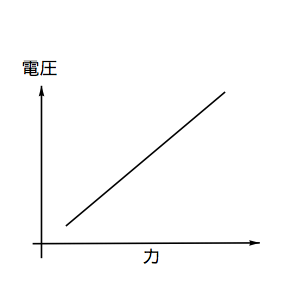
ところが我々が今求めたいのは、実際にスイングしているときに作用した力を知りたいのであって、出力電圧を知りたいわけではない。なので上のグラフは次のように考えておいたほうがいいだろう。単にXYの軸を変えて描いただけだが、最終的に求めたい方程式が違ってくるので念のため。
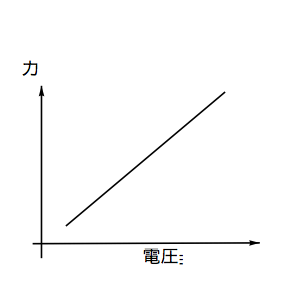
そこで何度か作用させる力を変えてみて、この直線を求めることにしよう。次の写真はラケットのグリップ部を万力ではさんで、ラケット先端に重りをつるして作用した力を再現している様子である。

(ラケットに作用する力測定の写真)
実験データから散布図をつくる
実験データ
何度か上の写真のような計測を行って得られた結果が次のようになった。この表を元にしてグラフを描いてみよう。ちなみにMathematicaで下のような表を作るには、「挿入」メニューから 「表・行列」を選べばよい。
データはリストにしたほうが、都合が良いだろうということはもう察しがついているのではないだろうか?
In[130]:=
![]()
Out[130]=
![]()
In[131]:=
![]()
Out[131]=
![]()
力の単位
ここで力の単位には、ニュートン[N]を用いる。バイオメカニクスの分野では、いや工学、物理の分野では単位系にはMKS単位系というものを用いることが慣例であり、また何も断わりがない限りこのMKS単位系を用いることになっている。Mは長さの単位のm、Kは重さの単位のKg、Sは時間の単位のsecondである。MKS単位系で計算される力の単位がニュートン[N]である。
1Nは、1Kgの質量をもつ物質が1秒間に、1m/![]() の加速度で動かされた際に物質に作用した力のことである。そこで測定した重量ではなく、ラケットに作用した「力」のデータで上で作った表を書き換えてみよう。
の加速度で動かされた際に物質に作用した力のことである。そこで測定した重量ではなく、ラケットに作用した「力」のデータで上で作った表を書き換えてみよう。
In[132]:=
![]()
Out[132]=
![]()
散布図を描く
散布図をMathematicaで描くのは簡単だ。ListPlot[]を使おう
![]()
ListPlot[]で散布図を描くにはまずデータを準備しなくてはならない。ListPlot[]では、描きたいデータを、{{x1,y1},{x2,y2},.....{xn,yn}}の形にして与えなければならない。先ほど作ったデータは同じ種類(次元)のデータが1つのリストになっていたので、これをそれぞれ、一番目の要素同士、二番目の要素同士…というふうに「転置」しなければならない。転置についてはすでに解説して理解しているはずである。
In[133]:=
![]()
Out[133]=
![]()
Transpose[]はリストデータを転置する。つまり、XYグラフを描きたい場合に、(x1,y1),(x2,y2).....のデータを作ってくれる。また軸にラベルをふるには、AxesLabelというオプションを使えばよい。
In[134]:=
![]()
Out[134]=
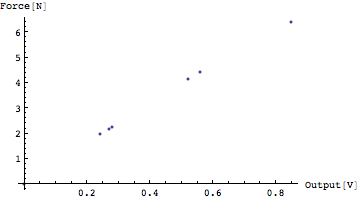
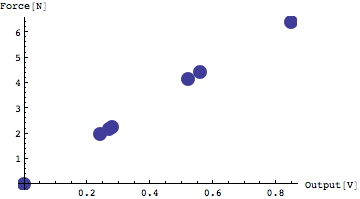
ちょっと点が小さすぎて見えない。点を大きく描こう。点を大きく描くにはPlotStyle->PointSize[x]を用いることはすでに習った。思い出そう。
In[135]:=
![]()
Out[135]=
プロットした点を線でつなぐには、Joined→Trueというオプションを使う。
![]()
Out[136]=
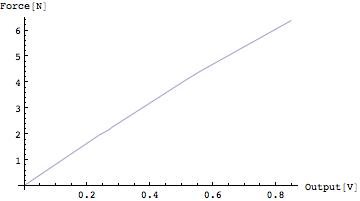
ほぼ直線だが、若干のジグザグがある。この点を代表する最も妥当な直線を探すというのが目的である。
最小二乗法
最小二乗法とは?
今やろうとしている問題を少し抽象化すると以下のようになる。
「x ={x1,x2,...xn}, y={y1,y2,...yn}で作られるデータに対して、xからyを推測することの出来るもっとも妥当な直線を見つけよ。」
もっとも妥当な直線というのは全ての点から、その妥当な直線に引いた垂線、つまりxiにおけるy^ - yiの差(これを残差, residualと呼ぶ)の和を最小にすればよいということに直感的に気がつくだろう。y^は「わいはっと」と読む。そして2次元平面のこのxyの関係を表すには直線を想定しているわけであるので、求めたい直線は
y = a x + b
の形をしていることになる。
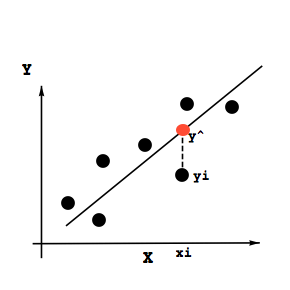
ではラケットのひずみの実験データを使ってこの直線を求めることにしよう。まずは残差の総和を求めるのだが、残差をそのまま足してしまうとプラスマイナスで相殺してしまう可能性があり、うまくない。そこで残差を足す際にはこれを二乗したものを足す。
そこでまずは求める式を定義しておこう
In[138]:=
![]()
In[139]:=
![]()
Out[139]=
![]()
この式のxの値に実験データである、アンプの出力電圧を代入した値がy^(yハットのつもり)になるわけだ。そこでこの式のxには実験データの出力電圧を代入してみよう。代入とは言ってみたがMathematicaの場合、これは置き換えにあたる。置き換えには通常、/. (スラッシュ+ピリオド)を後置形で使う。
In[140]:=
![]()
Out[140]=
![]()
ここで、x /.→voltageとしたが、voltageはリストだった。置き換えるものがリストの場合、置き換えられるべきxにはリストの要素全てを適用させる。次に、求めたyhatと実際に作用した力(実測値)との差分の二乗を足し合わせる。これには以下の1行だけでよい。Mathematicaはなんと楽なことか。これをC言語やC++で書こうとすると何行になるだろうか?
In[141]:=
![]()
Out[141]=
![]()
In[142]:=
![]()
Out[142]=
![]()
Simplify[]で簡略にすると上の残差の二乗和は,aとbで書きあらわされた式になっていることが分かる。最小二乗法とはこの式をa,bそれぞれで偏微分して0とおいた式を連立させて解くと求めることが出来る。
偏微分
「偏微分!、聞いたこともない」という人は軽くそのまま右から左に聞き流してもらってよい。a,bを変化させたときにもっとも残差の和が小さくなる。すなわち0になるという点を求めているということだけ覚えておいて欲しい。bの方は固定しておいてaだけを変化させたときに最も小さくなり、aの方を固定しておいてbを変化させて最も小さくなる、そんなa,bを求めようというわけだ。さてMathematicaで偏微分をするにはD[]を用いる。Dはderivative(微分の意味)の頭文字である。
![]()
![]()
式はこの場合には、残差の二乗和のSをaで偏微分し、同じくSをbで偏微分する、ということを行う。まずはaで偏微分してみる。
In[143]:=
![]()
Out[143]=
![]()
次にbで偏微分してみる
In[144]:=
![]()
Out[144]=
![]()
そして、「微分したものを0とおき、これを連立させて解く」という手順は次の1行で書くことが出来る。
In[145]:=
![]()
Out[145]=
![]()
Solve[]は連立方程式を解く関数である。すでにこれも習ったので使えるはずだ。
![]()
上の例では、a=7.51321, b=0.118581 と求まった。つまり求めたい方程式(1次式)の形は、
y = 7.51321 x +0.118581
ではこの定数が求まったところで実験データと求められた直線を同じグラフ上に表示して比べてみよう。
In[146]:=
![]()
Out[148]=
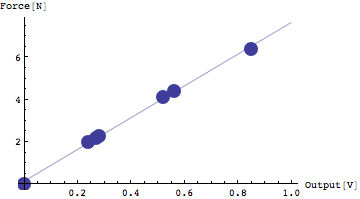
よく実験データを表す直線が求められたとみなしてもいいだろう。
相関係数
平均、分散、そして共分散
相関係数を簡単に説明すると、この最小二乗法の場合には求められた回帰直線のあてはまりの度合いを示すとでも言うべきか。この場合の相関係数は2変量(出力電圧、力)の散らばり具合、すなわち分散から求めることが出来る。2変量それぞれの平均値、分散は以下の式で表されることはすでに説明した。
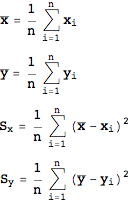
これに加えて、変量x、変量yの共分散というものが相関係数を計算するには必要となる。共分散は次の式によって与えられる。意味としてはお互いの変量間の相互の分散を示していると考えてもらいたい。共分散は判別分析の章で出てきたので参照してみてほしい.
![]()
上の式では、i番目のxi, yiを使ってΣの中を計算するが一方が平均値から偏っていればその掛け算の結果の絶対値は大きくなる。つまりx,yのそれぞれの平均値からの偏りがどちらも小さいときにのみ0になるということだ。
ここで相関係数は下記の式によって表される。変量x,yの共分散をxの分散とyの分散で割ったものである。
![]()
In[149]:=
![]()
Out[149]=
![]()
分散はVariance[]を用いる。
In[150]:=
![]()
Out[150]=
![]()
In[151]:=
![]()
Out[151]=
![]()
In[152]:=
![]()
Out[152]=
![]()
In[153]:=
![]()
Out[153]=
![]()
共分散を求める関数は、Covariance[]である。括弧内にリストを2ついれてやる。
In[155]:=
![]()
Out[155]=
![]()
In[156]:=
![]()
Out[156]=
![]()
相関係数が0.9以上となり、きわめて相関が高いことが分かった。つまりアンプの出力電圧からの力の推定は大変信頼性が高いことが示された。
スイングの計測
計測しよう
それでは実際にスイング中のラケットのひずみを計測してみよう。計測に用いた装置一式などは下の図に示した。こんな簡単な計測なのに結構な道具や装置が必要とされる。

(図:実験概要~ここではコンピュータにはデータを取り込まずオシロスコープでデータを眺めている)
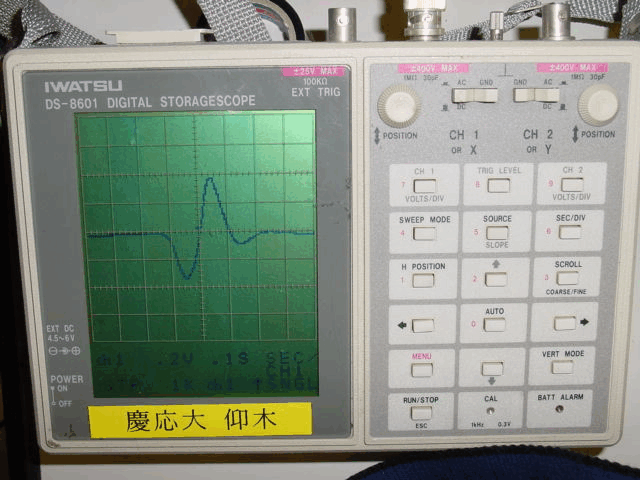
(図:ラケットスイング時の電圧変化=歪み)

(図:コンピュータに電圧の変化を取り込むための装置~AD変換器とコネクタボックス)
実験データの読み込み
推定式が求まったところで、実際にスイングしている最中にどの程度の力が作用しているのかを推定しよう。ファイル名、"RacketSwing.dat"という名前で実際にスイングをしたときのひずみ(電圧)のデータが準備してある。このデータを表示して、次にこの電圧データからインパクト時に作用した力の最大値を求めてみよう。準備されているデータはMathematicaのファイルであるので、Need[]もしくは、前置式では、<<で読み込める。
In[157]:=
![]()
Out[157]=
![]()
In[158]:=
![]()
実験データの確認
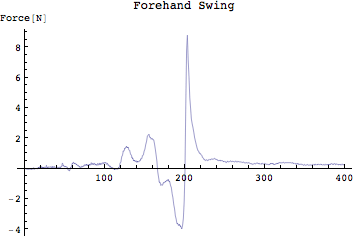
読み込んだファイルには、フォアハンドスイングのときの電圧変化(forehand)とバックハンドスイング(backhand)のときの電圧変化が記録されている。データの間隔(サンプリング時間)は、0.005[sec]、つまり200[Hz]である。一秒間に200回のサンプリングを行ったのである。
![]()
Out[161]=
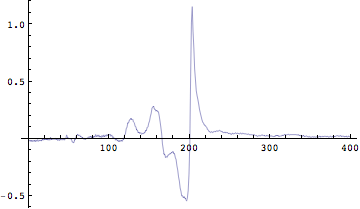
Out[162]=
フォアハンドスイングとバックハンドスイングでは、歪み方が逆の順番で表れていることに気が付いただろうか?では、どの程度の力がラケットシャフトに作用したのかを先ほどの回帰式から求めよう。先ほどの計算結果(solution)の各々の係数を回帰式にすればよく、その回帰式にこの電圧データを代入してやればよい。係数は求まっているので関数にしておこう。
推定式からスイング中の力を推定する
較正式の確認
今一度,推定式(較正係数)を確認しておこう.こでは,電圧から力を推定するための式であった.
In[163]:=
![]()
Out[163]=
![]()
この較正係数を使って,y = a x + b の形を作ってやる
In[164]:=
![]()
この較正式に実験データ(電圧)を入力して,力を求める.
In[165]:=
![]()
![]()
Out[167]=
Out[168]=
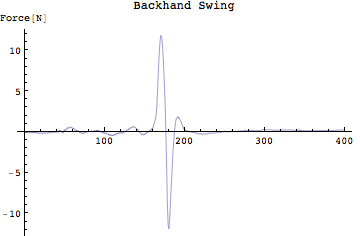
フォアハンドの場合には、最大で約8[N]。バックハンドの場合には最大で約±10[N]の力が作用していることがわかる。10Nというと9.8で割るとだいたい1Kg重の力ということになる。
最小二乗法 : Fit[ ]
すでに感づいている人もいるかとは思うが、こんな手順をいちいち順番にやらなくてもMathematicaは回帰直線を求める関数を準備してくれている。Fit[]がそれである。
![]()
ではFit[]を使って同じように最小二乗法で推定式が得られるだろうか?
In[169]:=
![]()
Out[169]=
![]()
In[170]:=
![]()
Out[170]=
![]()
{1, x}, x
の意味は、括弧の中{1,x}はxの0次の項、xの1次の項が式には必要です。最後のxは、その式の中での変数はxとします。というふうに定義する。偏微分を用いて計算して得られた係数と関数Fit[]を用いて得られた係数は一致した。すなわち関数Fit[]は同じことをやっているわけである。関数形の与え方がちょっと特殊だが、関数形のなかで独立変数の次元を書いておく。また1というのは定数項を含むという意味になる。
例題
問:前に用いたSFC学生の体力測定データのなかから、身長および体重を使って以下の回帰式を求めよ
(1)男子における身長から体重を推定する一次回帰式と相関係数
(2)女子における身長から体重を推定する一次回帰式と相関係数
最小二乗法(重回帰:打撃能力を測る)
はじめに
前節では得られる電圧から作用した力を推定する推定式を求めた。この際、独立変数は電圧であり従属変数は力(あるいはひずみ)であったと言える。このように一つの変数から他の変数を推定する上で、一次直線による推定式を求めることを一次回帰、または単回帰とも呼ぶ。これに対していくつかの変量からある変量を推定することを重回帰とよぶ。例えば、発掘された骨の長さ、太さ、歯の大きさなどの複数の変量から古代人の身長を知りたい、といった際には重回帰が必要とされる。
野球打撃成績データ
野球打撃成績データ
ここでは2004年のプロ野球パリーグ打撃個人成績データを用いて、打撃能力を推定することを試みよう。打撃能力といってもいろいろな要素が含まれるが、ここでは打点(各個人が打球を打ったことによって入った得点)に貢献するいくつかの変量から、打点推定式を算出し、それぞれの変量の重みについても考えてみよう。まずは2004年パリーグ打撃成績データを読み込む。
In[171]:=
![]()
Out[171]=
![]()
In[172]:=
![]()
In[173]:=
![]()
Out[173]//TableForm=
| \217\207\210Ê | \226¼\221O | \213\205\222c | \221Å\227¦ | \216\216\215\207\220\224 | \221Å\220È\220\224 | \221Å\220\224 | \223¾\223_ | \210À\221Å | \223ñ\227Û\221Å | \216O\227Û\221Å | \226{\227Û\221Å | \221Å\220\224 | \221Å\223_ | \216O\220U | \216l\213\205 | \216\213\205 | \213]\221Å | \213]\224ò | \223\220\227Û | \217o\227Û\227¦ | \222·\221Å\227¦ |
| 1 | \217¼\222\206 | \203_\203C\203G\201[ | 0.358 | 130 | 577 | 478 | 118 | 171 | 37 | 1 | 44 | 342 | 120 | 67 | 84 | 12 | 0 | 2 | 2 | 0.464 | 0.715 |
| 2 | \217¬\212}\214´ | \223ú\226{\203n\203 | 0.345 | 101 | 452 | 377 | 78 | 130 | 19 | 2 | 18 | 207 | 70 | 70 | 70 | 3 | 0 | 2 | 3 | 0.449 | 0.549 |
| 3 | \217é\223\207 | \203_\203C\203G\201[ | 0.338 | 116 | 498 | 426 | 91 | 144 | 25 | 1 | 36 | 279 | 91 | 45 | 49 | 22 | 0 | 1 | 6 | 0.432 | 0.655 |
| 4 | \210ä\214û | \203_\203C\203G\201[ | 0.333 | 124 | 574 | 510 | 96 | 170 | 34 | 2 | 24 | 280 | 89 | 90 | 47 | 9 | 0 | 8 | 18 | 0.394 | 0.549 |
| 5 | \221º\217¼ | \203I\203\212\203b\203N\203X | 0.32 | 108 | 503 | 459 | 70 | 147 | 29 | 1 | 6 | 196 | 51 | 87 | 35 | 3 | 5 | 1 | 11 | 0.371 | 0.427 |
| 6 | \230a\223c | \220¼\225\220 | 0.32 | 109 | 473 | 394 | 79 | 126 | 21 | 1 | 30 | 239 | 89 | 59 | 71 | 4 | 0 | 4 | 6 | 0.425 | 0.607 |
| 7 | \222J | \203I\203\212\203b\203N\203X | 0.317 | 96 | 431 | 378 | 58 | 120 | 27 | 1 | 15 | 194 | 63 | 42 | 44 | 2 | 2 | 5 | 10 | 0.387 | 0.513 |
| 8 | \203x\203j\201[ | \203\215\203b\203e | 0.315 | 130 | 552 | 457 | 89 | 144 | 31 | 1 | 35 | 282 | 100 | 77 | 86 | 5 | 0 | 4 | 8 | 0.426 | 0.617 |
| 9 | \225\237\211Y | \203\215\203b\203e | 0.314 | 128 | 569 | 506 | 67 | 159 | 42 | 1 | 11 | 236 | 73 | 82 | 47 | 10 | 2 | 4 | 2 | 0.381 | 0.466 |
| 10 | âE\225\224 | \213ß\223S | 0.309 | 120 | 529 | 457 | 82 | 141 | 22 | 1 | 26 | 243 | 75 | 69 | 62 | 2 | 5 | 3 | 7 | 0.391 | 0.532 |
| 11 | \212L\222Ë | \220¼\225\220 | 0.307 | 112 | 420 | 384 | 53 | 118 | 27 | 2 | 14 | 191 | 75 | 77 | 32 | 1 | 1 | 2 | 8 | 0.36 | 0.497 |
| 12 | \203Z\203M\203m\201[\203\213 | \223ú\226{\203n\203 | 0.305 | 125 | 530 | 443 | 86 | 135 | 24 | 0 | 44 | 291 | 108 | 110 | 70 | 14 | 0 | 3 | 0 | 0.413 | 0.657 |
| 13 | \221å\221º | \213ß\223S | 0.303 | 120 | 549 | 498 | 74 | 151 | 25 | 2 | 2 | 186 | 34 | 65 | 30 | 11 | 9 | 1 | 22 | 0.356 | 0.373 |
| 14 | \220ì\215è | \203_\203C\203G\201[ | 0.303 | 133 | 633 | 564 | 87 | 171 | 19 | 8 | 4 | 218 | 45 | 63 | 48 | 3 | 15 | 3 | 42 | 0.359 | 0.387 |
| 15 | \226k\220ì | \213ß\223S | 0.303 | 133 | 580 | 508 | 75 | 154 | 27 | 0 | 20 | 241 | 88 | 70 | 62 | 4 | 4 | 2 | 7 | 0.382 | 0.474 |
| 16 | \220V\217¯ | \223ú\226{\203n\203 | 0.298 | 123 | 544 | 504 | 88 | 150 | 28 | 3 | 24 | 256 | 79 | 58 | 15 | 9 | 12 | 4 | 1 | 0.327 | 0.508 |
| 17 | \220\205\214û | \213ß\223S | 0.293 | 118 | 473 | 389 | 55 | 114 | 20 | 0 | 6 | 152 | 40 | 60 | 50 | 3 | 27 | 4 | 0 | 0.374 | 0.391 |
| 18 | \203I\201[\203e\203B\203Y | \203I\203\212\203b\203N\203X | 0.289 | 128 | 526 | 477 | 70 | 138 | 28 | 0 | 24 | 238 | 71 | 87 | 40 | 7 | 0 | 2 | 4 | 0.352 | 0.499 |
| 19 | \222\206\223\207 | \220¼\225\220 | 0.287 | 133 | 559 | 502 | 70 | 144 | 22 | 3 | 27 | 253 | 90 | 108 | 39 | 11 | 3 | 4 | 18 | 0.349 | 0.504 |
| 20 | \226Ø\214³ | \223ú\226{\203n\203 | 0.285 | 132 | 559 | 505 | 67 | 144 | 24 | 1 | 9 | 197 | 62 | 108 | 47 | 4 | 0 | 3 | 4 | 0.349 | 0.39 |
| 21 | \215\202\213´\220M | \223ú\226{\203n\203 | 0.285 | 115 | 452 | 404 | 66 | 115 | 19 | 2 | 26 | 216 | 84 | 93 | 34 | 6 | 3 | 5 | 2 | 0.345 | 0.535 |
| 22 | \203t\203F\203\213\203i\203\223\203f\203X | \220¼\225\220 | 0.285 | 131 | 580 | 513 | 87 | 146 | 23 | 1 | 33 | 270 | 94 | 117 | 53 | 8 | 0 | 6 | 5 | 0.357 | 0.526 |
| 23 | \203Y\203\214\201[\203^ | \203_\203C\203G\201[ | 0.284 | 130 | 542 | 455 | 60 | 129 | 18 | 0 | 37 | 258 | 100 | 121 | 63 | 19 | 0 | 5 | 1 | 0.389 | 0.567 |
| 24 | \203o\203\213\203f\203X | \203_\203C\203G\201[ | 0.279 | 115 | 503 | 419 | 68 | 117 | 20 | 0 | 18 | 191 | 74 | 61 | 74 | 4 | 0 | 6 | 1 | 0.388 | 0.456 |
| 25 | \225½\226ì | \203I\203\212\203b\203N\203X | 0.279 | 124 | 424 | 377 | 50 | 105 | 18 | 7 | 6 | 155 | 39 | 69 | 30 | 6 | 9 | 2 | 10 | 0.34 | 0.411 |
| 26 | \203t\203\211\203\223\203R | \203\215\203b\203e | 0.278 | 130 | 503 | 439 | 70 | 122 | 35 | 2 | 16 | 209 | 65 | 66 | 58 | 2 | 1 | 3 | 1 | 0.363 | 0.476 |
| 27 | \222\206\221º | \213ß\223S | 0.274 | 105 | 462 | 387 | 59 | 106 | 16 | 1 | 19 | 181 | 66 | 88 | 73 | 1 | 0 | 1 | 0 | 0.39 | 0.468 |
| 28 | \226x | \203\215\203b\203e | 0.261 | 119 | 516 | 445 | 70 | 116 | 23 | 2 | 14 | 185 | 51 | 88 | 55 | 1 | 14 | 1 | 5 | 0.343 | 0.416 |
| 29 | \220Ô\223c | \220¼\225\220 | 0.259 | 122 | 436 | 374 | 68 | 97 | 18 | 2 | 9 | 146 | 41 | 87 | 42 | 2 | 15 | 3 | 16 | 0.335 | 0.39 |
| 30 | \213à\216q | \223ú\226{\203n\203 | 0.256 | 109 | 372 | 332 | 42 | 85 | 15 | 1 | 3 | 111 | 39 | 86 | 28 | 4 | 6 | 2 | 5 | 0.32 | 0.334 |
日本語の書かれているCSVファイルだが、読み込んでみると文字化けを起こしてしまっている。これはMathematicaの内部文字コードがUnicodeであるのに対して、読み込んだファイルの文字コードがWindowsで作られているために、ShiftJISになっているからである。正常に表示するには、ToCharacterCode[] とFromCharacterCode[]を用いて以下のようにする。
1行目は全部文字列なので、すべての列を文字コード変換し、それ以降の行は2列目と3列目だけ文字コード変換する。
In[174]:=

Out[174]=

![]()
| 順位 | 名前 | 球団 | 打率 | 試合数 | 打席数 | 打数 | 得点 | 安打 | 二塁打 | 三塁打 | 本塁打 | 打数 | 打点 | 三振 | 四球 | 死球 | 犠打 | 犠飛 | 盗塁 | 出塁率 | 長打率 |
| 1 | 松中 | ダイエー | 0.358 | 130 | 577 | 478 | 118 | 171 | 37 | 1 | 44 | 342 | 120 | 67 | 84 | 12 | 0 | 2 | 2 | 0.464 | 0.715 |
| 2 | 小笠原 | 日本ハム | 0.345 | 101 | 452 | 377 | 78 | 130 | 19 | 2 | 18 | 207 | 70 | 70 | 70 | 3 | 0 | 2 | 3 | 0.449 | 0.549 |
| 3 | 城島 | ダイエー | 0.338 | 116 | 498 | 426 | 91 | 144 | 25 | 1 | 36 | 279 | 91 | 45 | 49 | 22 | 0 | 1 | 6 | 0.432 | 0.655 |
| 4 | 井口 | ダイエー | 0.333 | 124 | 574 | 510 | 96 | 170 | 34 | 2 | 24 | 280 | 89 | 90 | 47 | 9 | 0 | 8 | 18 | 0.394 | 0.549 |
| 5 | 村松 | オリックス | 0.32 | 108 | 503 | 459 | 70 | 147 | 29 | 1 | 6 | 196 | 51 | 87 | 35 | 3 | 5 | 1 | 11 | 0.371 | 0.427 |
| 6 | 和田 | 西武 | 0.32 | 109 | 473 | 394 | 79 | 126 | 21 | 1 | 30 | 239 | 89 | 59 | 71 | 4 | 0 | 4 | 6 | 0.425 | 0.607 |
| 7 | 谷 | オリックス | 0.317 | 96 | 431 | 378 | 58 | 120 | 27 | 1 | 15 | 194 | 63 | 42 | 44 | 2 | 2 | 5 | 10 | 0.387 | 0.513 |
| 8 | ベニー | ロッテ | 0.315 | 130 | 552 | 457 | 89 | 144 | 31 | 1 | 35 | 282 | 100 | 77 | 86 | 5 | 0 | 4 | 8 | 0.426 | 0.617 |
| 9 | 福浦 | ロッテ | 0.314 | 128 | 569 | 506 | 67 | 159 | 42 | 1 | 11 | 236 | 73 | 82 | 47 | 10 | 2 | 4 | 2 | 0.381 | 0.466 |
| 10 | 礒部 | 近鉄 | 0.309 | 120 | 529 | 457 | 82 | 141 | 22 | 1 | 26 | 243 | 75 | 69 | 62 | 2 | 5 | 3 | 7 | 0.391 | 0.532 |
| 11 | 貝塚 | 西武 | 0.307 | 112 | 420 | 384 | 53 | 118 | 27 | 2 | 14 | 191 | 75 | 77 | 32 | 1 | 1 | 2 | 8 | 0.36 | 0.497 |
| 12 | セギノール | 日本ハム | 0.305 | 125 | 530 | 443 | 86 | 135 | 24 | 0 | 44 | 291 | 108 | 110 | 70 | 14 | 0 | 3 | 0 | 0.413 | 0.657 |
| 13 | 大村 | 近鉄 | 0.303 | 120 | 549 | 498 | 74 | 151 | 25 | 2 | 2 | 186 | 34 | 65 | 30 | 11 | 9 | 1 | 22 | 0.356 | 0.373 |
| 14 | 川崎 | ダイエー | 0.303 | 133 | 633 | 564 | 87 | 171 | 19 | 8 | 4 | 218 | 45 | 63 | 48 | 3 | 15 | 3 | 42 | 0.359 | 0.387 |
| 15 | 北川 | 近鉄 | 0.303 | 133 | 580 | 508 | 75 | 154 | 27 | 0 | 20 | 241 | 88 | 70 | 62 | 4 | 4 | 2 | 7 | 0.382 | 0.474 |
| 16 | 新庄 | 日本ハム | 0.298 | 123 | 544 | 504 | 88 | 150 | 28 | 3 | 24 | 256 | 79 | 58 | 15 | 9 | 12 | 4 | 1 | 0.327 | 0.508 |
| 17 | 水口 | 近鉄 | 0.293 | 118 | 473 | 389 | 55 | 114 | 20 | 0 | 6 | 152 | 40 | 60 | 50 | 3 | 27 | 4 | 0 | 0.374 | 0.391 |
| 18 | オーティズ | オリックス | 0.289 | 128 | 526 | 477 | 70 | 138 | 28 | 0 | 24 | 238 | 71 | 87 | 40 | 7 | 0 | 2 | 4 | 0.352 | 0.499 |
| 19 | 中島 | 西武 | 0.287 | 133 | 559 | 502 | 70 | 144 | 22 | 3 | 27 | 253 | 90 | 108 | 39 | 11 | 3 | 4 | 18 | 0.349 | 0.504 |
| 20 | 木元 | 日本ハム | 0.285 | 132 | 559 | 505 | 67 | 144 | 24 | 1 | 9 | 197 | 62 | 108 | 47 | 4 | 0 | 3 | 4 | 0.349 | 0.39 |
| 21 | 高橋信 | 日本ハム | 0.285 | 115 | 452 | 404 | 66 | 115 | 19 | 2 | 26 | 216 | 84 | 93 | 34 | 6 | 3 | 5 | 2 | 0.345 | 0.535 |
| 22 | フェルナンデス | 西武 | 0.285 | 131 | 580 | 513 | 87 | 146 | 23 | 1 | 33 | 270 | 94 | 117 | 53 | 8 | 0 | 6 | 5 | 0.357 | 0.526 |
| 23 | ズレータ | ダイエー | 0.284 | 130 | 542 | 455 | 60 | 129 | 18 | 0 | 37 | 258 | 100 | 121 | 63 | 19 | 0 | 5 | 1 | 0.389 | 0.567 |
| 24 | バルデス | ダイエー | 0.279 | 115 | 503 | 419 | 68 | 117 | 20 | 0 | 18 | 191 | 74 | 61 | 74 | 4 | 0 | 6 | 1 | 0.388 | 0.456 |
| 25 | 平野 | オリックス | 0.279 | 124 | 424 | 377 | 50 | 105 | 18 | 7 | 6 | 155 | 39 | 69 | 30 | 6 | 9 | 2 | 10 | 0.34 | 0.411 |
| 26 | フランコ | ロッテ | 0.278 | 130 | 503 | 439 | 70 | 122 | 35 | 2 | 16 | 209 | 65 | 66 | 58 | 2 | 1 | 3 | 1 | 0.363 | 0.476 |
| 27 | 中村 | 近鉄 | 0.274 | 105 | 462 | 387 | 59 | 106 | 16 | 1 | 19 | 181 | 66 | 88 | 73 | 1 | 0 | 1 | 0 | 0.39 | 0.468 |
| 28 | 堀 | ロッテ | 0.261 | 119 | 516 | 445 | 70 | 116 | 23 | 2 | 14 | 185 | 51 | 88 | 55 | 1 | 14 | 1 | 5 | 0.343 | 0.416 |
| 29 | 赤田 | 西武 | 0.259 | 122 | 436 | 374 | 68 | 97 | 18 | 2 | 9 | 146 | 41 | 87 | 42 | 2 | 15 | 3 | 16 | 0.335 | 0.39 |
| 30 | 金子 | 日本ハム | 0.256 | 109 | 372 | 332 | 42 | 85 | 15 | 1 | 3 | 111 | 39 | 86 | 28 | 4 | 6 | 2 | 5 | 0.32 | 0.334 |
打者の成績に関して
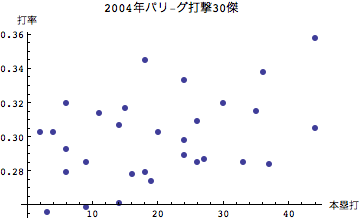
打率に関する観察
打率がもっとも高い選手のことを首位打者とよぶが、打率は安打に当然関連するので横軸に安打数、縦軸に打率を描いてみよう。
任意の列データのみを抜き出す。さらに先頭行のインデックスも取り除く。それをListPlotで表示する。
In[181]:=
![]()
Out[183]=
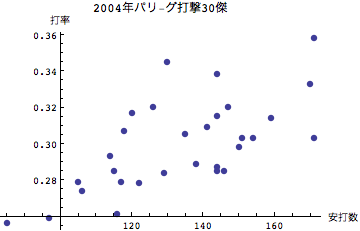
当然といえば当然だが、安打数が多い選手ほど打率もよい傾向にあることがわかる。次に本塁打および二塁打と打率についてみてみよう。
In[184]:=
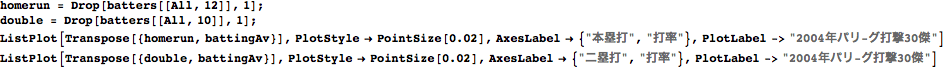
Out[186]=
Out[187]=
本塁打については傾きが若干小さいようにみえるが、二塁打については二塁打本数が多いほど打率も高い傾向にあるようだ。
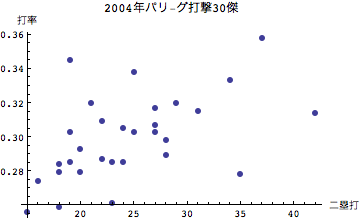
打点に関する観察
打点は塁上にランナーがいる場合、あるいは自分自身を含めて自らのバッティングによって得点したかどうかを示す指標である。従ってよく打つのだが塁にランナーがいないために得点には結びつかない場合には打点が向上することはない。逆の見方をすればチャンスに強いという打者は塁にランナーがいるときに打てる打者であるといえる。では打点とそのほかの変量との関係をみてみよう。
In[188]:=

Out[189]=
Out[190]=
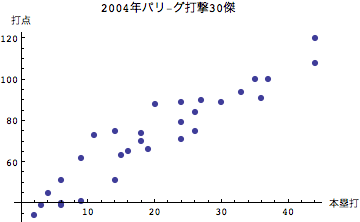
Out[191]=
グラフから読み取れるように、本塁打を量産する打者ほど打点が大きいということが分かる。安打、二塁打については散らばりが大きく、必ずしもそれが直接打点に結びついていないこともここからわかる。ホームランバッターが重宝される理由はここにあるといえる.
重回帰の考え方
安打や本塁打などの打者の「打つ」という行為の結果として現れる打点を推定することを考えよう。打点は、安打(シングルヒット)、二塁打、三塁打、本塁打などをあわせた結果として得られる数量であると考えるならば、それらをまとめて打点を推定する推定式を作ろう、というのが目的である。仮に安打と本塁打の2つから打点を推定することを考えると、3次元平面を考えて、X軸には安打数を、Y軸には本塁打数を、Z軸には打点の軸をそれぞれとった空間を考える。この空間上で安打と本塁打が分かれば打点を推定できる式を見つけることが命題となる。
一次回帰(単回帰)の場合には、2次元平面に散らばるデータに対して、説明変数(独立変数)Xと目的変数(従属変数)Yとおき、XからYを推定するもっとも適切な直線を見つけ出した。これが2つの説明変数(独立変数)から、1つの目的変数を推定するということになった場合には、3次元空間上を2つに横切る平面の方程式を見つけることにほかならない。つまり下のように3次元空間を区切る平面の方程式で言えば、a=2, b=3, cの各係数を求めることが重回帰方程式を求めるということに相当する。
In[193]:=
![]()
Out[193]=
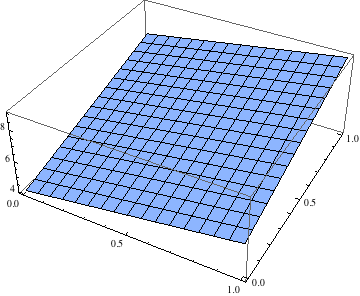
打点は、そのときどきの安打・二塁打・三塁打・本塁打が影響を及ぼすことは間違いない。また打点と各変量間の関係を散布図で見て分かったように、ある程度安打、本塁打と打点の間には関係がありそうだ。そこでここでは安打と本塁打を説明変数(独立変数)として、目的変数(従属変数)には打点をおき、安打と本塁打数から打点を推定する式を求めよう。
一次回帰のところでも登場したFit[]を用いれば簡単に重回帰方程式が求められる。
Fit[]を使った重回帰式の算出
Fitによる重回帰方程式の算出法
関数Fit[]を用いた重回帰方程式の算出は簡単だ。変数の並び方だけ注意すればよい。今一度Fitの使い方を見ておこう。データは2重リストで与える必要がある。そして各リスト要素の一番最後には目的変数(従属変数)がきて、それよりも前のデータのならびには、変量を指定しておく。
In[194]:=
![]()
では安打と本塁打から打点を推定する推定式を求めよう。変量hit(安打)と変量homerun(本塁打)によって、打点(ribby)を求めるには以下のようにする。
In[195]:=
![]()
Out[195]=
![]()
簡単に求めることが出来た。ためしに、安打数が141本、本塁打数が26本の人はどの程度打点をあげることが出来るのかという予測を行うには以下のようにする。
In[196]:=
![]()
Out[196]=
![]()
/. (スラッシュピリオド)は、置き換えを意味し、式中のx1とx2を141と26で置き換えよ、というのが上の説明となる。実はこの安打141本、本塁打26本は打率10位の礒部選手の値であるが、実際の礒部選手の打点は75であり、8.4本の差が認められる。
では、全選手のデータを用いて、推定がうまくできているかどうかを確認しよう。実際の値と推定値の差をすべて足し合わせると正負の値で差し引き0になる可能性もある。このような場合には誤差を二乗してそれを足し合わせるという手法が常道だ。
In[197]:=
![]()
Out[197]//TableForm=
| 171 | 44 | 120 | 118.665 | 1.33487 |
| 130 | 18 | 70 | 68.2359 | 1.76413 |
| 144 | 36 | 91 | 100.6 | -9.59988 |
| 170 | 24 | 89 | 85.284 | 3.71604 |
| 147 | 6 | 51 | 51.3254 | -0.325407 |
| 126 | 30 | 89 | 87.4496 | 1.55042 |
| 120 | 15 | 63 | 61.4836 | 1.51645 |
| 144 | 35 | 100 | 98.9397 | 1.06032 |
| 159 | 11 | 73 | 61.7525 | 11.2475 |
| 141 | 26 | 75 | 83.4664 | -8.46637 |
| 118 | 14 | 75 | 59.469 | 15.531 |
| 135 | 44 | 108 | 112.287 | -4.28693 |
| 151 | 2 | 34 | 45.3933 | -11.3933 |
| 171 | 4 | 45 | 52.2571 | -7.25714 |
| 154 | 20 | 88 | 75.8084 | 12.1916 |
| 150 | 24 | 79 | 81.7405 | -2.74052 |
| 114 | 6 | 40 | 45.4787 | -5.47872 |
| 138 | 24 | 71 | 79.6145 | -8.61445 |
| 144 | 27 | 90 | 85.6581 | 4.34192 |
| 144 | 9 | 62 | 55.7745 | 6.22551 |
| 115 | 26 | 84 | 78.8599 | 5.14011 |
| 146 | 33 | 94 | 95.9736 | -1.97363 |
| 129 | 37 | 100 | 99.6025 | 0.397503 |
| 117 | 18 | 74 | 65.9326 | 8.06737 |
| 105 | 6 | 39 | 43.8842 | -4.88417 |
| 122 | 16 | 65 | 63.4981 | 1.5019 |
| 106 | 19 | 66 | 65.6439 | 0.356061 |
| 116 | 14 | 51 | 59.1147 | -8.11466 |
| 97 | 9 | 41 | 47.4474 | -6.44739 |
| 85 | 3 | 39 | 35.3601 | 3.63987 |
表形式で表された結果のデータ並びは以下のとおりである.
1列目:実際の安打数
2列目:実際の本塁打数
3列目:実際の打点数
4列目:推定式による打点数
5列目:実測打点数と推定打点数の差
では,標準誤差はというと
In[198]:=
![]()
Out[198]=
![]()
標準誤差は,約1.2点となりなかなか精度よく推定が出来ているといえる.実際には,推定式を作ったデータではなくそれ以外の標本でチェックをしなければならないことを憶えておこう.
最小二乗法の詳細データ:LinearModelFit[ ]
LinearModelFit[ ]の利用
最小二乗法で推定式を求める際に,実際の研究の場ではその推定式の精度や,残差なども知っておく必要がある.おそらくどのようなデータであっても計算上は数式を求めることができるのであるが,その精度を検討する上では,どうしても最小二乗法で求めた式に付随する記述統計量も必要である.
これを知るには,LinearModelFit[ ]という関数を使うと便利である.
LinearModelFit[ ]は,最小二乗法で式を求めることはもちろん,記述統計量も同時に出力してくれる
In[203]:=
![]()
In[204]:=
![]()
Out[204]=
![]()
In[205]:=
![]()
Out[205]=
| DF | SS | MS | F Statistic | P-Value | |
| x1 | 1 | 2898.03 | 2898.03 | 59.3912 | 2.74224*10^^-8 |
| x2 | 1 | 10659.3 | 10659.3 | 218.447 | 1.83942*10^^-14 |
| Error | 27 | 1317.48 | 48.7956 | ||
| Total | 29 | 14874.8 |
In[206]:=
![]()
Out[206]=
![]()
表から,決定係数(相関係数の二乗)が,RSquared -> 0.911429となっており,なかなかの精度で推定式が得られていることがここから分かる.
数値積分(床反力データから跳躍高を求める)
垂直跳び床反力データから跳躍高を求める
床反力の計測
本節では単純な運動と考えられる垂直跳びを題材に床反力の計測から重心の変位、速度、加速度を算出する。Mathematicaを使って数値積分を行い、計測データである床反力から最高到達点の高さを求める。また垂直跳びにおいてなされる仕事、パワーなど関連する変数なども計算を通して理解する。垂直跳びを観察するには、ジャンプしている最中の動作を映像によって観察する方法と、ジャンプしている(離陸前の)最中の床反力を観察する2つの手法がある。前者は運動において外に現れる位置情報を情報源とする。後者は運動において観測される力を情報源とする。前者をキネマティクスといい、後者をキネティクスとよぶ。今回はキネティクスが話題である。
計測実験
フォースプレート
フォースプレートは床反力を計測する計測器のことである。もっとも広く普及しているのはスイスのキスラー社製のフォースプレートである。フォースプレートの原理はピエゾ効果に依存している。フォースプレートの四隅に納まっている水晶の結晶に力が加えられると電荷が放出される。この電荷量を電圧に変換して取り出すことによってそこに加えられた力の大きさが分かるというものである。次の写真は慶應義塾大学所有のフォースプレートである。

(フォースプレート写真)
実験データ
それでは実験データを読み込んで垂直跳びにおいて観察される床反力を眺めてみよう。実験データファイル名は、"vjump023.dat"である。単なるテキストファイルなのでTextファイルを読み込む方式である、ReadList[]を使う。そして計測データの内訳は以下のとおりである。
計測データは今回次の通り。力の単位は[N]。
1)absolute time (s) :時間
2) Fx[N] :X軸方向の力
3)Fy[N] :Y軸方向の力
4)Fz[N] :Z軸方向の力(鉛直成分)
5)Fx12[N] :
6)Fx34[N] :
7)Fy14[N] :
8)Fy23[N] :
9) Fz1[N] : センサ1のZ軸方向の力
10) Fz2[N] : センサ2のZ軸方向の力
11) Fz3[N] : センサ3のZ軸方向の力
12) Fz4[N] : センサ4のZ軸方向の力
実験データの読み込み
In[207]:=
![]()
Out[207]=
![]()
In[208]:=
![]()
データがきちんと読み込まれたかを確認する。リストデータの次元を知るには関数Dimensions[]を使う。
In[209]:=
![]()
Out[209]=
![]()
1250 * 12のリストのリストが返ってきた。1250行×12列といってもよい。実際に使いたいのはこのうち一列分のデータに相当する。したがっていったんこの読み込んだデータの転置行列をとる。
In[210]:=
![]()
鉛直方向(上下方向)の力のみを観察
鉛直方向の力の成分は4番目にあるはずだ。垂直跳びは上下方向の運動だといえるだろうから、まずはこの鉛直方向の力成分のみ描画してみる。リストデータをグラフにするのには、もうご存知のListPlot[]を用いる。
In[211]:=
![]()
![]()
Out[213]=
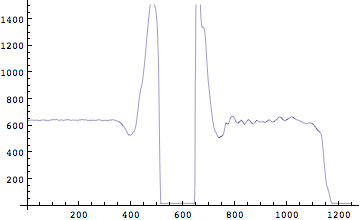
ところでリストデータの1番目は時間である。ここで横軸を時間、縦軸を力にして描画してみよう。
In[214]:=
![]()
![]()
Out[215]=
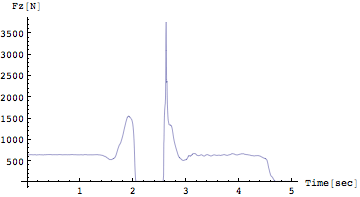
軸にラベルを描いて、縦軸のレンジをデータ全てをカバーするように指定したらグラフ自身が小さくなってしまった。実はMathematicaは通常何も指定しないとデータの変化幅がもっとも適切なグラフを出力してくれる。この例の場合2.5[sec]近辺で大きな衝撃力(3500N以上)が記録されているためこの部分はdefaultの図では省いてしまっている。人が見てもっともデータの変化を捉えやすいように操作してくれたのだ。
他の軸のデータ
次にせっかくのデータなのでFx()、Fy()、Fz(鉛直方向成分)全てのデータを描画してみよう。
![]()
Out[216]=
Out[217]=
Out[218]=
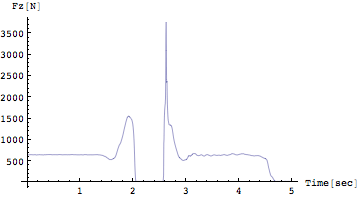
地面反力の鉛直成分を観察する
運動方程式で考える
地面反力の鉛直成分を観察するとどんなことが分かるだろうか?地面反力とは地面が物体を押し上げている力と考えてもらえばよい。そして垂直跳びの運動は次の図のように行われるといえる。重心がまず沈み込み、そしてやがて徐々に上昇していき、離陸して最高到達点であるh2まで跳ぶ。
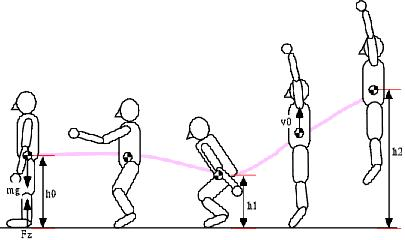
ここでは運動方程式を使って説明していくことにしよう。運動方程式とは物体の運動状態を表す記述方法であり、これが古典物理学の基礎とも言える。今、初期状態である静止している状態を考えるとこの被験者に作用している力は、重力と床から押し上げられている力(Fz)の2つしかない。そしてこの2つが同じ大きさで向きが逆であることから釣り合いの状態にあり、静止している。従って式で書くと
![]()
ここで力はベクトル(大きさと方向を持つ量)であるから、式中の符号は向きをも表していることに注意しなければならない。
静止状態から、次に重心が下に動いたということは物体(人)が下向きに運動したということである。つまりmgとFzの大きさの均衡が崩れてmgのほうがFzよりも大きくなったということになる。逆の言い方をすると、Fzがmgよりも小さくなったといえる。この沈み込む動作のことを抜重と呼ぶ。この間、体重計に乗っているとすると針は体重よりも小さくなる。
柔道などの組み手系の格闘技では相手が抜重した瞬間に足を払うことがよいとされる。その理由は今体重計のことを説明したようにみかけ上体重が小さくなったようにみえ、そのときであれば小さな力で相手を倒すことが出来るからである。
グラフでFzの変化を見てみよう。すると静止状態からFzが減少していることがみてとれる。これが抜重の状態である。次に加重がくる。加重していくということはFzの方がmgよりも大きくなっていき、重心が上方に移動していくということである。
ニュートンの第2法則
力と加速度
力と加速度との関係はどうなっているだろうか?高校の理科1(今も理科1なんてのはあるのだろうか?)で習ったと思うが、ニュートンの第2法則は以下のように説明されている。

「質量mの物体に加速度aが生じた際には、その物体には力Fが作用している」と読める。
ところで、静止状態に観測されたFzはちょうどmgとつりあっていたことはすでに述べた。従って重力加速度g (= 9.8m/![]() )で割れば、実はこの人の体重が求まる。最初の方のデータ100個の平均値をとってみて、体重を求めてみよう。
)で割れば、実はこの人の体重が求まる。最初の方のデータ100個の平均値をとってみて、体重を求めてみよう。
In[219]:=
![]()
Out[219]=
![]()
静止状態ではmgとFzがつりあっていた、ということで運動方程式を書いてみたが、より正確に記述しよう。運動方程式は何も静止して釣り合っている状態だけを記述するものではない。重心の位置座標をxと表すと、重心の持つ加速度は、![]() と表される。ここで
と表される。ここで![]() はxの二階微分であり加速度を意味する。ここでは先ほども出てきているのでこれをaで表すことにする。
はxの二階微分であり加速度を意味する。ここでは先ほども出てきているのでこれをaで表すことにする。
![]()
従って重心の加速度aは次のようになる。
![]()
先ほど、被験者の体重は求めた。そこでこの重心の持つ加速度を計算しよう。
In[220]:=
![]()
![]()
Out[222]=
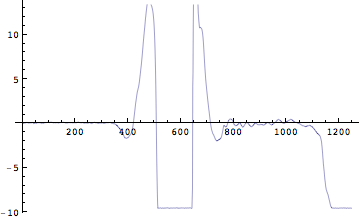
なるほど、動いていないときには重心の加速度は0である。重心の上向きの加速度の最大値はいくつだろうか?
In[223]:=
![]()
Out[223]=
![]()
下向きの加速度の最大値は?
In[224]:=
![]()
Out[224]=
![]()
これは空中期には下向きの重力加速度のみが作用しているということを示している。
加速度・速度・変位
積分の物理的理解
加速度を積分すると速度になる、とは高校の物理で習っただろうか?速度が変化するのは、物体に外から力が働いたにほかならない。物体に力が働かなければその物体は静止しているか、もしくは同じ速度で(等速度)で動きつづけるというのがニュートンの第1法則である。従って加速度を受けた物体は速度変化を起こす。ここで観察しているのは実は重心の変化であり、上で求められた加速度も重心の加速度であるため、これを積分すると重心の速度が算出される。
では積分はどうやって行うのだろうか?連続系の場合には積分は以下の式で高校で習ってきたのではないだろうか?
![]()
微分・積分をMathematicaは数式計算として扱うことが得意だ。ためしに数学にあるような微分積分の問題をMathematicaにやらせてみればよい。今のところ証明可能な積分関数は全てMathematicaで解く事が出来るといわれている。我々、すなわち数学を道具としてしか扱わないような者にとっては解けない式はまずなかろう。ちなみにMathematicaでの積分はIntegrate[],Nintegrate[]である。
![]()
例えば、
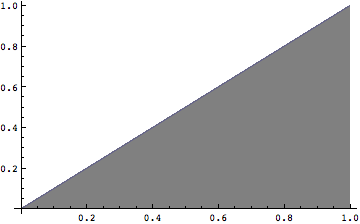
![]()
をxについて0から1まで積分してみよう
In[226]:=
![]()
Out[226]=
In[227]:=
![]()
Out[227]=
![]()
図から分かるように底辺1、高さ1の三角形の面積に相当するわけなので、面積は当然1/2だ
次は、三角関数を試しに積分してみよう
![]()
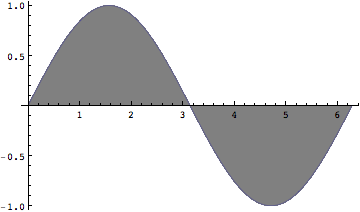
In[228]:=
![]()
Out[228]=
In[229]:=
![]()
Out[229]=
![]()
今度はプラスマイナスが相殺されて面積は0となることは明らかだ
![]()
積分を実行する関数には,Integrate[ ]のほかに,NIntegrate[ ]が存在するが,この2つの関数には引数として式が与えられなければならない。ところが今我々が持っているのは数値列、すなわち鉛直方向の力、加速度の数値データである。従ってこの数値データを数値的に積分しなければならないので、これらの関数群を用いることは出来ない。
数値積分で加速度から速度・変位を求める
シンプソンの台形公式
計算機上ではすでにこれまで見てきたようにデータは連続量(式で表現可能)ではなく離散量(数値列)である。従って積分は数値積分という方法を用いる。数値積分では微小区間の面積を求めてそれを次々に足していくという簡単なものである。微小区間の面積を求めるには一般的にシンプソンの台形公式として知られる公式を用いる。

![]()
シンプソンの台形公式を関数化しよう
In[230]:=
![]()
全体の面積Sを求めるには?
C言語をやってきた人は次のように関数を作るだろう
In[231]:=

In[232]:=
![]()
![]()
Out[233]=
時間軸を横軸にとるには、元のデータの時間軸情報を使う。
![]()
![]()
![]()
エラーがでた。Transpose[]が出来ないと言っている。よく見ると時間軸のデータ個数と速度のデータ個数が異なっている。
In[235]:=
![]()
Out[235]=
![]()
In[236]:=
![]()
Out[236]=
![]()
なぜなら、積分を行った関数ListIntegrate[]をよく見れば分かることだが、今の時刻のデータと次のデータの区間の面積を計算するときにIteratorがリストの長さよりも1つだけ少ない回数だけ繰り返されている。そこで出来上がったデータ(ここでは速度)は元データの時間軸を組にするとTranspose[]をすることが出来ないのである。
そこで時間軸を合わせることにしよう。合わせると言っても積分して速度を計算して一つデータが欠落したので、ないものを付け足すよりも元のデータを1つ減らす方が無難であろう。そこで元データの時間軸に相当するデータを1つ削除してからプロットしてみる。
![]()
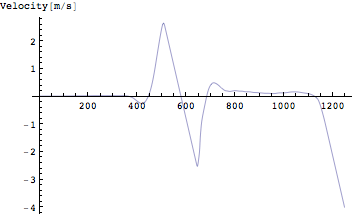
Out[238]=
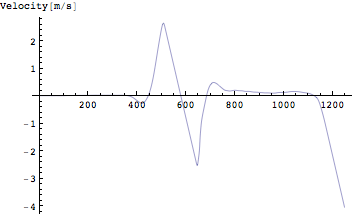
こうすると速度曲線が時間軸に対して描かれた。ここでただ眺めるのではなく物理的な目でこのグラフを眺めてみよう。すると速度の変化には正のピークと負のピークがあることに気が付くだろう。正の速度ピークはどこだろうか?ここで正の向きは上向きと定めた。上向きの速度が最も大きくなるのは、当然飛び出す瞬間であることに気が付くだろう。
なぜなら、飛び出したあとは重力加速度によって徐々に速度は減じることは明らかである。すなわち速度の正のピークの瞬間に離地するのである。次に速度が負のピークに至る前に0を横切っている。速度が0というのはどこだろう?そう、最も高く飛び上がった時間である。なぜなら、最も高い位置(最高到達点)に達した瞬間速度の向きが正から負へ変わる。当然そのとき速度は0になる。負のピークはどうだろうか?考えてみよう。
次に変位を求めよう。「変位」という言葉を使い慣れていない人には違和感があるかもしれない。「位置」と言ったほうがいいかもしれないが、「変位」といった場合にはきちんと定義された座標系での「位置」を指していることが多いようである。ここでは力学の慣例に従って「変位」という言葉で説明する。
「変位」は「速度」の積分によって求めることが出来る。シンプソンの台形公式を説明した図で、理解を促すとすると横軸が時間で、縦軸が速度のグラフを考えると歩いた距離は曲線ではさまれた面積となる。従って変位は速度の積分によって求めることが出来る。
では実際に変位を求めてみよう。
In[239]:=
![]()
![]()
Out[240]=
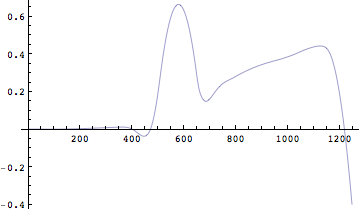
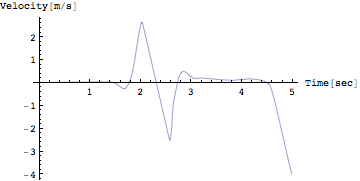
上方向に移動したあとで正のピークを迎えたあとで、また下方へと動き再び上昇している。なんだか変だ?これはなぜだろう?
最初の床反力のグラフを再度見てみよう。
![]()
Out[241]=
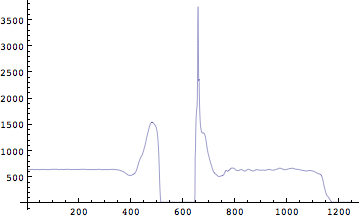
こうしてみると何か気が付いただろうか?力の波形を見てみると、床反力は動き始めで徐々に減少したあと次に増加に転じてピークを迎えたあと、今度は0になってしまう。床反力が0二になったということはすなわちフォースプレートに立っていた人が離地したことを意味している。従ってもとになっているデータはここまでが人間の運動を表しているわけで、これ以降は実は記述することは出来ない。ではここまでの時間でよいので、全てのデータを重ねてみよう。まず飛び出した瞬間の時刻、あるいはデータの並びで言えば何番目のデータが飛び出した瞬間になるのかを知らなくてはいけない。簡単な方法を教えよう。
ListPlot[]のグラフをダブルクリックしてオブジェクト指定した状態でCtl(コントロールキー)を押してグラフの上にカーソルを持っていく。するとグラフ上の座標の取得ができることに気がつくだろう。
Mathematica流で積分計算
リスト演算関数を駆使する
上は繰り返し計算、ここではForを使った一般的なプログラミング言語の手続きと同じだ。それでは面白くない。ここはひとつ、Mathematica流に積分計算プログラムを書いてみよう。それにはリスト演算を使う。説明は後回し、まずはMathematica流のプログラムを見てもらおう
In[242]:=

速度を計算してみよう
In[243]:=
![]()
![]()
Out[244]=
全く同じ結果が得られていることが分かる。Mathematica流で書けばわずか1行でプログラミングが可能だ。今度は速度を積分して位置を計算してみよう
In[245]:=
![]()
![]()
Out[246]=
これも同じグラフが描けた。ここで作成した関数は, FoldList, Map, Paritionという関数を使っている。Mapはもうお馴染みあろう。Partitionも一度出てきているが引数の与え方で動作が異なる。
In[247]:=
![]()
Out[247]=
![]()
In[248]:=
![]()
Out[248]=
![]()
引数を2つ与えると上のように、リストから成分を2つづつ取り出すが、1つだけずらして取り出す、といった分け方が出来る。
In[249]:=
![]()
Out[249]=
![]()
FoldList[]はリストのなかに式を適用するが、このときリストの要素の前から順に式を適用し、それを次々に後に作用させるということをやってくれる。
In[250]:=
![]()
In[251]:=
![]()
Out[251]=
![]()
これは、0,0+1, 0+1+2, 0+1+2+3, 0+1+2+3+4, 0+1+2+3+4+5を計算してくれたということになる。
微分と積分
加速度、速度および変位の関係は下のようになっている。時間で微分することで変位から速度、加速度を求めることが出来る。逆に加速度を時間で積分することで速度、変位が求まる。

変位の微分を求めるということは、変位のグラフを描いたときにある瞬間における変位の変化分、すなわち「傾き」を求めることに相当する。傾きは実は単位時間あたりの変位の変化なのでこれは速度にあたる。加速度は同様にして速度の単位時間あたりの変化分に相当する。時々刻々の曲線の傾きを調べることが微分をするということになる。
仕事とパワー(仕事率)
仕事とパワー(仕事率)
最後に仕事とパワーに関して説明する。仕事とは、力×距離、で求まる物理量である。どのくらいの力を出して移動したのかということ。いくら力を出していても、力の方向に全く移動していないときにはその力による仕事は0である。
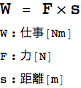
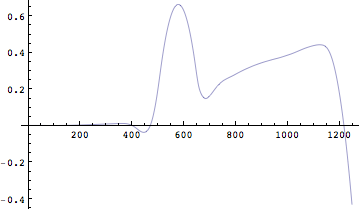
次にパワーは、単位時間あたりに、どのくらい仕事をしたのかということである。つまり上の仕事を要した時間で割ったものになる。
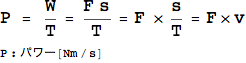
パワーとは、結果的にみると力×速度で求まる物理量である。これは人間の動きに例えるならば「瞬発力」に相当する。いくら大きな力を発揮できても、のんびりとゆっくり力を発揮する場合にはパワーが大きいとはいえない。なんとなく会社の仕事ぶりも同じことが言えるような気がする。「あいつはパワーがある」という場合には仕事をてきぱきと素早くそれもたくさんさばく人のことを指しているように思えるからである。
垂直跳びでなされる仕事とパワー
それでは実際に垂直跳びのときの仕事とパワーを鉛直成分について計算してみよう。まずは仕事から。仕事は力と距離の積である。距離とはこのとき鉛直成分を考えているのですでに求めてある。上下方向の変位に相当する。これを掛けてやればよい。
In[252]:=
![]()
![]()
エラーが出た。どうやら、2つのリストの長さが違うといっている。先ほど説明したように積分計算のときにもとのリストの長さに比べて一回積分をするたびに1つデータが欠落していく。そこで加速度の2回積分を行って求められた変位は加速度データに比べて2個データが不足している。そこで変位のデータ長にあわせることにする。
In[253]:=
![]()
In[254]:=
![]()
今度もエラーが出てきた。だがこれはよく見るとエラーではなく警告メッセージである。PowerというMathematicaが準備しているオブジェクトにそっくりのものを定義しているが大丈夫か?と言ってきているだけであるので無視してよい。powerの計算の時にはもとの力データと速度のデータ長の差は1なので1つだけ後ろからデータを削除していることに注意せよ。それぞれのグラフを表示してみよう。
![]()
Out[255]=
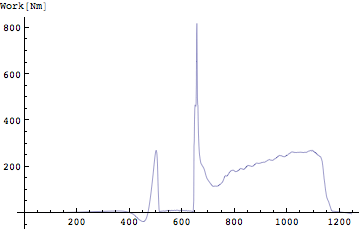
Out[256]=
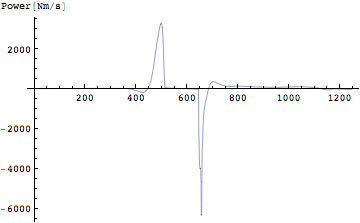
実際には飛び出す瞬間までのデータを表示すればよいので前半部分だけを描くことにする。
![]()
Out[257]=
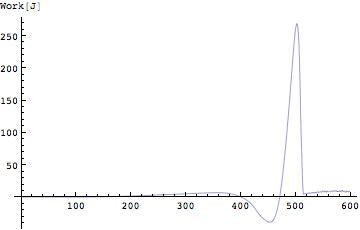
Out[258]=
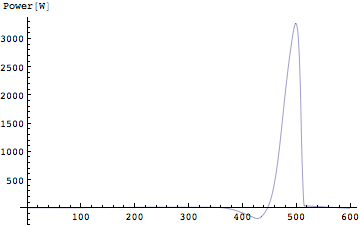
ちなみに、[Nm]は実際には[J](ジュール)。[Nm/s]は[W](ワット)として用いるのが普通である。
例題
数値微分(映像データから加速度を求める)
垂直跳び映像データから速度・加速度を求める
Kinematics とKinetics
本章は前章の続きで垂直跳びを題材にしている。前節は垂直跳びのときにフォースプレートを使って計測された床反力から重心の加速度と速度、変位を求め、さらに垂直跳びの際の仕事、パワーを計算した。こうした力を扱う力学のことを、Kinetics(キネティクス:運動力学)とよび力を考えない力学分野のことをKinematics(キネマティクス、運動学)とよぶ。本節はその垂直跳び中に横から撮影した映像を元にして、運動学的(キネマティクス)な分析を行ってみる。つまり力に関しては考えをめぐらさない。
関節座標を映像から知る
つま先、かかと、足首、膝、腰、首、頭といった身体各部位、ここでは関節で考えることにする。この関節の座標が全部分かればそれらの座標をつなぐことで線画を作ることが出来る。ある時刻の図を1枚分を作ったら、次のコマ、さらに次のコマと線画を作ってしまい出来上がったら「パラパラアニメ」のように連続してみればあたかも動いているように見える。これがアニメーションの原理である。
そしてこのようにパラパラアニメのように,関節座標がわかり,それが時間的に連続して得られたらそこから速度,加速度といった変数が算出される.したがって関節の座標を知ることから始めなければならない。少し考えれば分かることであるが、この関節座標、各コマでそれぞれの座標を求めなければならない上に運動時間全体にわたってそれを繰り返さなければならない。家庭で使うような民生用のビデオカメラでさえも1秒間に30フレーム(正確には60フィールド)の撮影を行っているのでこの作業はかなり大変だ。そこでこんな大変な作業をやってくれるソフトウェアなどがすでに準備されている。これを使ったデータを転用したい。
デジタイズデータの読み込み
In[259]:=
![]()
Out[259]=
![]()
In[260]:=
![]()
Out[260]=
![]()
Excelなどで作ったCSVフォーマット( comma-separated format)のファイルを読み込む場合には、Import[]を用いればよい。CSVファイルなので、オプション"CSV"を与える。
In[261]:=
![]()
リストのリストが読み込まれた。もとのデータの並びは下記のようになっている。
時間[msec], 関節1のX座標[mm], 関節1のY座標[mm], 関節2のX座標[mm], 関節2のY座標[mm], 関節3のX座標[mm], 関節3のY座標[mm]
1行目には,上記の列詳細が含まれているので,1行目だけをまず取り除かないといけない.
これがエクセルによってCSVファイルに保存されたわけである。そして関節1から関節3は、足首、膝、股関節の各関節のいずれかである。
読み込まれたリストのうち内包される一つのリストが、エクセルの1行に相当するわけである。またそれがすなわち、ある瞬間の各関節座標のX,Yを示している。そこで時間に沿ってこれを表示させるためには一旦転置させたほうが簡単だ。
In[263]:=
![]()
するとcoords2の1番目は時間、2番目は関節1番目のX座標、3番目は関節1番目のY座標のというふうに時間に沿ったならびに変わった。ではこれを順番に表示してみよう。
時系列データの表示
あとで分かりやすくなるように色つきで描画する

Out[264]=
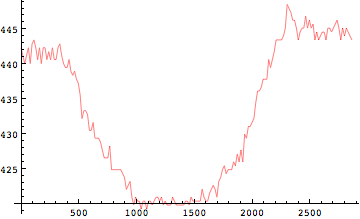
Out[265]=
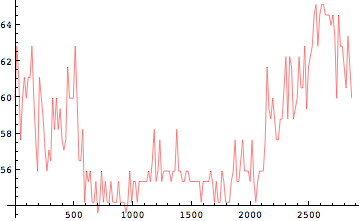
Out[266]=
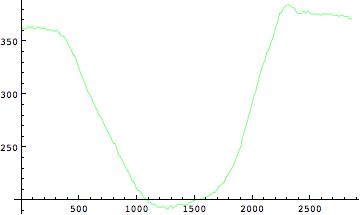
Out[267]=
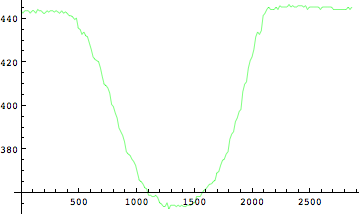
Out[268]=
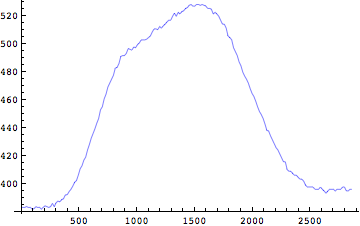
Out[269]=
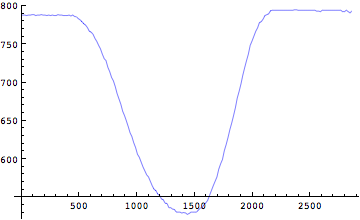
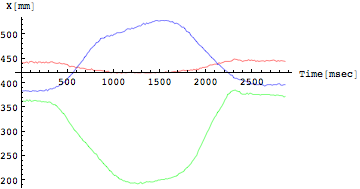
[[2]],[[4]],[[6]]番目がそれぞれのX座標
[[3]],[[5]],[[7]]番目がそれぞれのY座標
であるから、同じX座標はまとめて、Y座標もまとめて表示してみよう。
In[274]:=
![]()
Out[274]=
Out[275]=
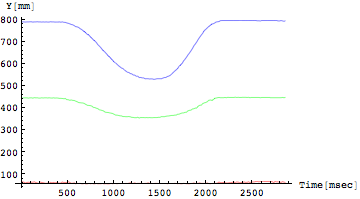
赤(関節1)、緑(関節2)、青(関節3)のそれぞれが足関節、膝関節、股関節のどこに相当するかを知るにはY座標(鉛直方向)をみればよい。直立したときに最も下部にあるのが足首であるから、すなわち赤が足首関節、最も高い位置にある青が股関節、緑が膝関節になるわけである。
1フレーム分のアニメーションをつくる
リストcoordsの中に内包される一つのリストが「ある瞬間の各関節座標」を示していることを先ほど説明した。従ってこの1時刻分のデータを用いれば、ある瞬間の姿勢を描画できることになる。早速これに挑戦してみよう。
Mathematicaでは、時系列データを表示するためのListPlot[]や関数を表示するためのPlot[]、3次元データを描画するためのListPlot3d[]などグラフの描画には数多くの関数が用意されている。しかし、ここでは線画(これをスティックピクチュアとよぶ)によってアニメーションを描くには、グラフィックス原始関数(Graphics Primitives)というより低レベルな関数を用いて描画することにする。すでに諸君はグラフィックス原始関数を学んでいるのでもはや恐れることはない。
線を描くにはLine[]を用いる
![]()
In[276]:=
![]()
Out[276]=
![]()
関数Line[]だけでは描画は出来ない。これはそれぞれの座標を線でつなぐよ、という命令を作ったに過ぎない。そこでこれがグラフィックスオブジェクトであるということを関数Graphics[]で命令する。さらにこれを関数Show[]で表示する。ちょっと面倒だが致し方ない。
In[277]:=
![]()
Out[277]=

![]()
ここでいうprimitivesというのはグラフィックスの種類だと思ってもらえればよい。そしてこのprimitivesにはグラフィックスの色なども指定することも可能だ。
In[278]:=
![]()
Out[278]=

![]()
Showのオプションにはグラフィックスを描画する際に付随的なものを指定することも出来る
In[279]:=
![]()
Out[279]=
Mathematicaの全てのグラフィックスは実はこのような低レベル関数を組み合わせて実現されている。ちょっと前置きが長くなったのでこれらを使って垂直跳びのアニメーションを一こま分作ろう。
ところで、線画にするには以下の順序で線を描かなくてはならないことにはすぐ気が付くだろう。
(1)股関節と膝関節を線で結ぶ
(2)膝関節と足関節を線で結ぶ
単にこれだけをプログラムでかけばよい。関数にしてみよう。与えるデータの並び方によく注意してプログラムを書く。もう一度念のために確認しておくと、
[[1]]時刻
[[2]]足関節X座標
[[3]]足関節Y座標
[[4]]膝関節X座標
[[5]]膝関節Y座標
[[6]]股関節X座標
[[7]]股関節Y座標
In[280]:=
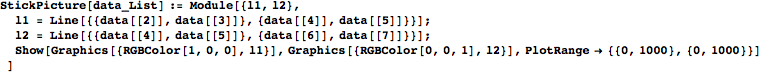
In[281]:=
![]()
Out[281]=

連続して描画しよう
1フレーム分が描画できたのならば、それをフレーム分だけ繰り返して描画すれば全体のアニメーションが完成する。繰り返しには色々な方法があることは既に学んだが、ここではAnimate[]を使ってみよう。
In[284]:=
![]()
In[288]:=
![]()
Out[288]=
ムービーに変換
描画した後に、{-Graphics-,-Graphics-,....}というものが返されたということに気が付いただろう。これはつまり、グラフィックスオブジェクトが返されたということなのでこれを変数animに格納したということはあとでこれを再利用することも可能だということだ。そこでこれを使ってGIFアニメーションを作ってみよう。GIFアニメーションを作るにはMathematicaのデータをGIFフォーマットに変換することが必要だ。これには関数Export[]を用いる。
![]()
In[289]:=
![]()
Out[289]=
![]()
In[295]:=
![]()
Out[295]=
![]()
各関節の速度・加速度
位置座標が求められたが、時々刻々変化するこの位置座標から各関節の速度と加速度を求めることが出来る。
速度とは、「単位時間あたりの移動距離(位置座標の変化)」
加速度とは、「単位時間あたりの速度変化」
で定義される。難しそうな定義を持ち出すならば、速度とは変位の微分であり、加速度とは速度の微分である。垂直跳びの力波形から変位を求めた際には、2階積分を行った。力波形はすなわち加速度波形と同じ時系列を示し、その積分は速度を意味していた。そして速度の積分は変位であった。つまりここでも微分/積分の意味がでてくるのである。
速度
では時々刻々と変化する位置座標を元にして、速度を求めてみよう。
時刻tの時点の速度=(時刻(t+δt)の位置座標-時刻(t-δt)の位置座標)/(2*δt)
である。データの1列目が時刻であったことを思い出せばこの場合の単位時間は各々の時刻間の時間幅であることに気が付くだろう。従ってこれを計算するには次のような関数を作ればよいことになる
In[296]:=

股関節座標から股関節座標のX方向速度およびY方向速度を求めてみよう。
In[297]:=
![]()
![]()
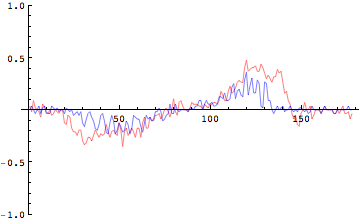
Out[307]=
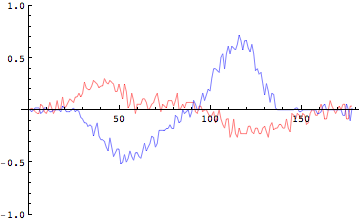
非常にギザギザした波形が得られた。ノイズが乗っているようにも見える。実はこれが映像解析の問題点なのである。映像解析によって関節座標から微分によって速度、加速度を求めるには、単位時間で割り算を行う。時間が微小であるが故にこの計算においてもともとの位置座標の精度が悪いとそこで誤差が増大されてしまうのである。これを微分誤差とよぶ。膝関節、足関節も同様に計算をしてみよう。
In[308]:=
![]()
![]()
Out[312]=
In[313]:=
![]()
![]()
Out[317]=
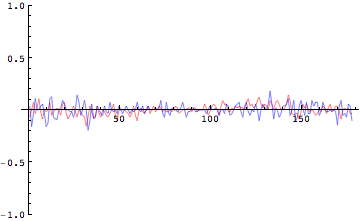
加速度
大変、ノイズの大きな波形である速度が得られたわけであるが、ここまでくるとさらにこれを微分する加速度はもっとノイズが増大されるだろうということにすでに気がついている人もいるかもしれない。とにかくどれほどノイズは増大されるのかを確認するためにも、加速度を求めてみよう。
In[318]:=
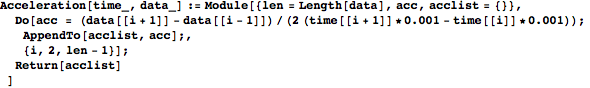
速度を計算する際に、データが2つ欠落したことに注意して繰り返し計算を行う必要がある。従ってここでは時間軸データの最後を一つ削って(Drop[XXXX,-1])から加速度を求めた。
In[319]:=
![]()
![]()
Out[323]=
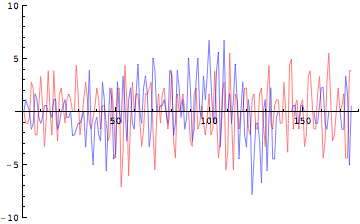
もうノイズだらけで何が何だかわからない波形になってしまっている。Y軸方向の速度は減少、増加、減少と繰り返しているのであるから、それをもたらしたはずの加速度も速度変化に先んじて変化が起こっていなければならないはずだが、ノイズだらけで全くそのような兆候も見受けられない。同様に膝関節、足関節も見てみよう。
In[324]:=
![]()
![]()
Out[328]=
In[329]:=
![]()
![]()
Out[333]=
理論通りにはなかなかうまくいかないということが分かっただろうか?
数式処理(代数方程式・運動方程式を解く)
方程式を解く
スポーツデータを解析するには,必ずモデルが必要である.ここでいうモデルとは,物理モデルであったり数理モデルであったりその形態はいくつもとり得るが,考え方の論拠でありそのモデル範疇でデータを論じることになる.得られるデータは数値であったり,記号であったりするかもしれないが,いずれにせよ数式によって記述しないと定量的な解析はできない.
そこで本章では数式処理について学び,代数方程式の解法,微分方程式の解法などを学ぶことにする.
まずは代数方程式に関する操作について紹介していく事にする.
式の操作
Mathematicaでは,式の操作を行う関数がいくつも用意されている.知っておくと便利なこともあるので紹介しておきたい.ヘルプには、式の操作という項目があるのでこれを参照して欲しい。
式の係数を求める
式の中の特定の変数についての係数を求めるための関数が用意されている.
例えば、y = ![]() Coefficient[]を使う
Coefficient[]を使う
In[334]:=
![]()
In[335]:=
![]()
Out[335]=
![]()
複雑な式のなかに出てくる係数でも簡単に求まる.
In[336]:=
![]()
Out[336]=
![]()
In[337]:=
![]()
Out[337]=
![]()
分数式の操作
分数の形に式が展開されて,そのなかで分母と分子をそれぞれ取り出したいときには, Denominator[]、Numerator[],を用いる
分母を知る
In[338]:=
![]()
Out[338]=
![]()
In[339]:=
![]()
Out[339]=
![]()
分子を知る
In[340]:=
![]()
Out[340]=
![]()
ほかにも,分母,分子のなかを全て展開する,ExpandNumerator[]やExpandDenominator[]などもあるので、ヘルプを参照して欲しい。
式が等しいかどうかを知る
式が果たして同じものかどうかを確かめるための関数,Equal[]が用意されている.通常は、これは==(イコール2つ)で使用する
In[341]:=
![]()
Out[341]=
![]()
In[342]:=
![]()
Out[342]=
![]()
In[343]:=
![]()
Out[343]=
![]()
一次方程式
簡単な一次方程式の解法はすでに学んだはずである.多くの場合は、関数Solve[ ]を使えばよい。例えば,x + 1 == 0の解を求めるには,次のようにして答えを求めればよい
In[344]:=
![]()
Out[344]=
![]()
ここで,得られた解はリストになっているので答えの-1を取り出すには次のようにすればよい
In[345]:=
![]()
Out[345]=
![]()
In[346]:=
![]()
Out[346]=
![]()
返ってきたリストはリストのリストになっていて,更にその中身を指定する必要がある.同じような関数として,Root[ ]という関数も用意されている.
Root[ ]は,k字の代数方程式,f(x) == 0 の根を求める.使う場合には純関数を用いることで表現できる.
In[347]:=
![]()
Out[347]=
![]()
In[348]:=
![]()
Out[348]=
![]()
二次・三次・四次方程式
二次方程式の解の公式
二次方程式についてもすでにこの授業で一度出てきた.解の公式をMathematicaによって確認しよう![]()
In[349]:=
![]()
In[350]:=
![]()
Out[350]=
![]()
確かに,中学校の時に勉強した二次方程式の解の公式と同じ形が得られた。前の例に従ってこの2次方程式の2つの解を取り出すには次のようにすればよい
In[351]:=
![]()
Out[351]=
![]()
In[352]:=
![]()
Out[352]=
![]()
ここで,得られた解の活用方法について一つ学んでおく。
res2[[1,1,2]]は解の一つであるが、ここでもしも、a=6, b = 7,c =2であったとする。これは次の式の展開である。
In[353]:=
![]()
Out[353]=
![]()
これを単純に解くにはSolveに代入してもよい
In[354]:=
![]()
Out[354]=
![]()
あるいは,次のようにしても答えが得られる
In[355]:=
![]()
Out[355]=
![]()
In[356]:=
![]()
Out[356]=
![]()
/. (スラッシュ,ドット)は、置き換えを意味する。式中のシンボルを/.以下で指示したものに置き換える、という意味を持つために {a → 6,b→7,c→2}と指示すると解が同様に求まる。/. は関数の後置形と呼ばれ、これを別の形式で表すと、ReplaceAll[ ]という関数となる。
例題
問:次の式の,xを解け![]()
問:次の式の,xを解け。この答えで出てくるものはなんだろうか?
x^2+1==0
三次・四次方程式
Mathematicaでは,三次方程式や四次方程式,さらに高次の代数方程式も同じようにして解くことができる。
In[357]:=
![]()
Out[357]=
![]()
In[358]:=
![]()
Out[358]=
![]()
特別な式の場合
Cos[x]==x
ある種の特別な式の場合には,Solve[]では解けないことがある.Cos[x] ==xという式の場合がそれに当てはまる
In[359]:=
![]()
![]()
Out[359]=
![]()
この場合,代数的に(数式で)解くのではなく、数値的に解くと解が求まる
In[360]:=
![]()
Out[360]=
![]()
どのようにして求めたかというと,FindRoot[]はニュートン法という方法を用いている.ニュートン法とは数式処理ではなく、数値計算の一手法であるが初期値1.0から解を探索せよ。ということを上の式では指示している。次の例では別の式の解を求めている
In[361]:=
![]()
Out[361]=
![]()
In[362]:=
![]()
Out[362]=
![]()
言うまでもなく,解はSolve[]で求められた、50の平方根である。しかしニュートン法では1つしか解が求まっていない。これは求める解の最初の推定値であり、50近辺から解を求めていく。そこで一つだけが解として求まっている。使用するときには注意が必要である。考え方は次のとおり
(1)根の最初の初期値,a0を決める
(2)近似のよりよい推定値を,a1,a2,a3....を次のルールで次々に求めて,最終的に十分信頼のできる精度の解を得る
![]()
詳しくは,ニュートン法というキーワードで書籍を参考にしてほしい.
連立方程式
連立一次方程式
連立方程式を解く際にも,Solve[]を使うことが可能である.
![]()
In[363]:=
![]()
Out[363]=
![]()
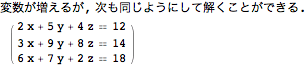
In[364]:=
![]()
Out[364]=
![]()
ベクトル表記を使ったSolve[]の使い方
次の連立一次方程式

In[365]:=
![]()
Out[365]=
![]()
当然,{{3,1},{2,-5}}.{x,y}は,ここで解いている連立方程式2つの式のことである
In[366]:=
![]()
Out[366]=
![]()
微分
数式処理のなかでもMathematicaが得意なものに一つに微分積分がある.そのうちまずは、微分を紹介することにする。微分は関数D[ ]または、Dt[ ]を使う。
全微分 Dt[ ]
例題: y = xを微分する
In[367]:=
![]()
Out[367]=
![]()
In[368]:=
![]()
Dt[]は高校の数学までで習った微分(ここでは全微分と呼んでいる)を行ってくれる.
例題: y = Sin[x]を微分する
In[369]:=
![]()
Out[369]=
![]()
Sin[x]の微分はCos[x]である
In[370]:=
![]()
Out[370]=
![]()
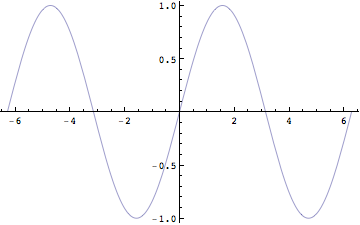
Cos[x]の微分は,-Sin[x]である.
図で理解しよう.まず微分は接線を求めること,あるいは極限を求めることだったことを思い出せば、微分する、すなわち導関数を求めるということは、各点における接線を求めることである。
In[371]:=
![]()
Out[371]=
In[372]:=
![]()
Out[373]=
In[374]:=
![]()
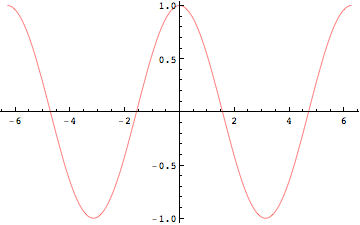
Out[374]=
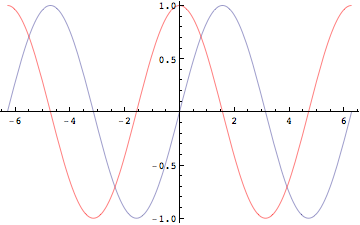
微分して得られた関数は,そのxにおける接線の傾きを示しているため,例えば上の例では時刻0の時の接線の傾きは最も大きく,その値が1であったことがわかる.同様に、Sin[x]の関数が最も大きな値をとる時刻(Pi/2)の時刻では接線の傾きは0である。
例題: y = (x+1)(2x + 3)(3x +4)
因数分解された状態で微分する場合には,各因数を微分したものと,他の因数の積を足し合わせることを覚えているだろうか?
In[375]:=
![]()
Out[375]=
![]()
In[376]:=
![]()
Out[376]=
![]()
最初から展開してから,Dt[]にかけてももちろん同じ答えが返ってくる
In[377]:=
![]()
Out[377]=
![]()
In[378]:=
![]()
Out[378]=
![]()
![]()
自然対数の底eの関数を微分するとどうなるか?
Eがなんだったか忘れてしまった人は、「ふなひとはちふたはち…」で無限に続く数、で丸暗記したことを思い出そう。
In[379]:=
![]()
In[380]:=
![]()
Out[380]=
![]()
![]()
In[381]:=
![]()
Out[381]=
例題
問:色々な式を微分してみよ
Log[x]
ArcCos[x]
…
積分
積分もMathematicaは得意中の得意である。現在、積分可能であると証明されている関数形については、全てMathematicaは積分できるとうたわれている。
不定積分 Integrate[]
高校までの数学で習った積分(不定積分)は,関数Integrate[]で実現可能である.
In[382]:=
![]()
例題:∫xdx
In[383]:=
![]()
Out[383]=
![]()
例題: ∫Sin[x]dx
In[384]:=
![]()
Out[384]=
![]()
Sin[x]の不定積分は,-Cos[x]であることが分かった.微分のときはどうであったか,思い出せ.
例題: ![]()
一般的なべき乗関数の場合にはどうなるか?
In[385]:=
![]()
Out[385]=
![]()
定積分 Integrate[]
区間を決めて積分を行う,定積分も同じくIntegrate[]を用いる
例題: ![]()
関数 y = xを区間{0,1}で積分する
In[386]:=
![]()
Out[386]=
![]()
積分は面積であったことは思い出したであろうか?図で説明するとどうなるか?やってみよう.
In[387]:=
![]()
Out[387]=
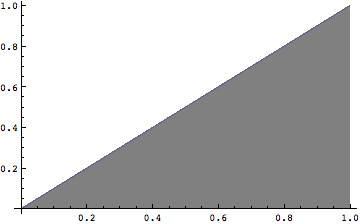
y=xの式の直線から下の部分で囲まれた面積.すなわち上の図で灰色に塗られている部分の面積は1/2であることを確認せよ.
![]()
In[388]:=
![]()
Out[388]=
![]()
In[389]:=
![]()
Out[389]=
Sin[x]を0から2Piまで積分するということは,上の図で灰色で囲まれた面積を0から1までの区間で足し合わせていくということなので,正負の符号を考えると,足し合わせると結局0になるわけである.
例題
問:時速300Kmで走行する新幹線のぞみが、2時間15分走ると何Km走行したことになるか?速度の積分が位置であることを考えればこれは積分で得られる。Integrate[]を使って、2時間15分後の位置を算出せよ。
また、初期位置が300Km地点からの距離を算出するにはどうすればよいだろうか?
ヒトの運動解析
ヒトの運動を解析する上で,ここまで紹介した代数方程式の解法や数値方程式の解法を用いることが出来る.以下では,簡単な例でヒトの解剖学的構造,
てこ
てことは,力の大きさを変換させる機能をもつ棒を意味する。てこには、1,2,3種のてこがあり、人体にはいくつものてこがあり、筋肉の収縮力をてこの作用で変換している。てこには、支点、力点、作用点がある。支点は回転の中心となる点。力点は力がはたらく点。作用点は加えた力が作用する点である。
第1種のてこ
第1種のてこは,支点が力点と作用点の間に存在するてこである.もっとも簡単な例は、シーソーである。
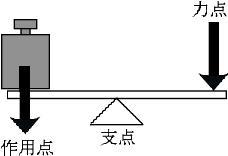
ペンチなんかもこれに相当するてこである。
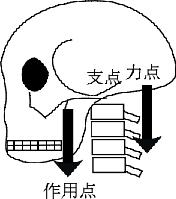
人間の体のなかでは、頭蓋骨を支えている首の部分が第1種のてこに相当する。頭部の重心が側面から見ると耳の辺りにあるため、首の後ろの筋肉がなければ、頭蓋骨が前方に倒れてしまう。そこで首の後ろの筋肉は常に頭蓋骨を持ち上げるために引っ張っている。
第1種のてこが,つりあっている、すなわち静止しているとすれば、回転中心である支点の周りで右回りの回転と、左回りの回転がつりあっていることを意味する。この回転の力のつりあいに関しては、「モーメント」という概念を使う。
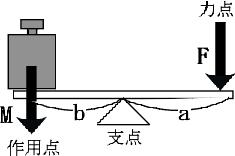
Mb = Faが成り立つということになる.やじろべえもこの原理である。外力(M)に抗して筋肉が力(F)を発揮する場合には、通常 a < b であることが多いため、発揮している力でみると、M < Fのことが多い。
次の例を見ればそれがわかるだろう。
例題
問:上の図で、前腕には張力計(引っ張り力を測定する装置)が手首に取り付けられていて、目盛りには20Kgfが示されているとする。以下のパラメータの場合、つりあい状態にある上の状態で上腕三頭筋が前腕を引っ張っている力、Fがいくつかを計算で求めよ。なお、a,bは、支点からM、Fの力のそれぞれの向きに対して直角に測定した距離である。
a = 2.0cm
b = 23.0cm
M = 20Kgf ( = 196N)
F = ???
第2種のてこ
第2種のてこは,作用点が支点と力点の間にあるてこをさす.栓抜きや、手押し車がこれに相当する.
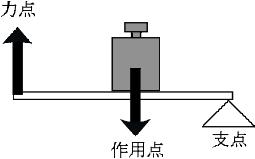
つま先立ちをする際には,アキレス腱を通じて下腿の裏側の筋肉がかかとの骨に力を及ぼしている.このとき第2種のてこの原理が働いている
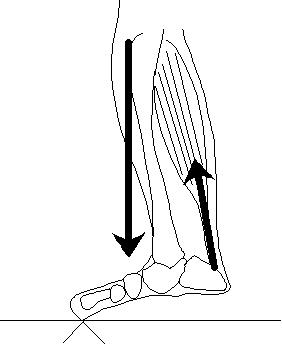
第2種のてこの場合には,a > b, F < Mが常に成り立っている.従って,小さな力で大きな力に抗するようなときに向いているといえる。上の例では、体重という大きな負荷を小さな筋肉であるアキレス腱で持ち上げることが可能になっている。
第3種のてこ
第3種のてこは,力点が支点と作用点との間にあるてこのことをさす.
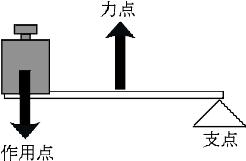
前腕を肘関節回りで屈曲させるときには第3のてこがはたらいているといえる.
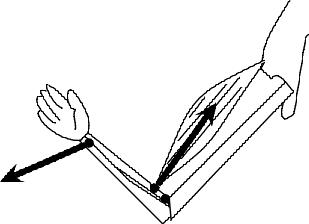
この場合,a < b , F> Mであるので,常に発揮する力以下の力しか外に現れない(作用点に作用しない)ため,筋肉の出せる力よりも軽いものしか動かせないことになる.
脊椎の静力学
てこがどんなものか,だいたい理解できたところで運動中に人体に働いている力を静力学の立場で解析してみよう.
例題:バーベルを持ち上げる人
この例題は,バイオメカニクス(嘉数侑昇,横井浩史監訳,NTS)のp117-p119である。重量挙げを行う人の脊椎において、どの程度の力が作用しているのかを解析的に求めた上で、それに実際の人体のパラメータをいれて、推定してみる。
まずは、重量挙げを行おうとしている選手のイメージを想像してもらいたい。次の図をみると腰に負担がかかりそうな姿勢であることは容易に想像がつくであろう。そして、この姿勢で今選手の動きが静止していると仮定しよう。
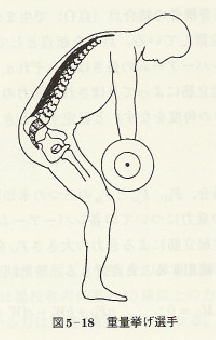
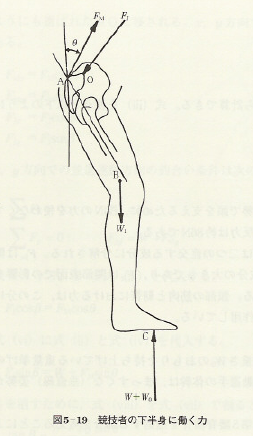
次に,下半身,脊椎部分に注目するとそこに働く力は、
体重+バーベルに相当する地面反力 : W+W0
下腿の重量:W1
上体の前傾角度:θ
仙骨と第5腰椎結合点に作用する圧縮力:Fj
体幹を支えるために脊柱起立筋によって発揮される力:FM
Oという回転の中心(下半身全体と上半身がここで結合されている支点であると考える)によって上図の姿勢を保っていると考える。すると、FMという脊柱起立筋によって骨盤が引っ張られて姿勢が維持できていることが分かるだろう。
上の図をさらに簡略化して描いたものが次の図となる。ここで、「釣り合っている」ということは、
(1)回転をしていない
(2)並進運動もしていない
ということになるので、回転の要素(モーメント)も釣り合っている上、上下方向の力の成分と左右方向の力の成分のそれぞれは、釣り合っているということになる。つまり力はベクトルなのでその方向も考慮すれば差し引き0であることを意味する。
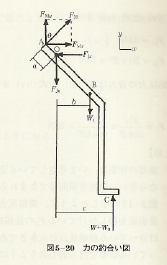
解法:Mathematicaを使って数式のままで解いてみる
まずは回転については釣り合っているということと,その回転の中心はOにしたので,Oを中心とした正逆方向の回転要素が釣り合っていることを式で表す
![]()
In[390]:=
![]()
Out[390]=
![]()
今知りたいのは,どのくらいの力で脊柱起立筋が引っ張ってくれて,身体を支えてくれているかを知りたいのであるからFMについて解けばよい
In[391]:=
![]()
Out[391]=
![]()
実際に得られた答えの中の未知変数,a,b,c,W,W1,W0を与えれば実際の力の大きさが分かる。しかしこのままでは、回転は起こしていない、という条件のみの計算しか行っていないので、上下方向、左右方向(並進運動)も釣り合っているという条件式を解く必要がある。
まずは,FMの左右方向成分(x方向成分)、上下方向成分(y方向成分)を求めておく
In[392]:=
![]()
![]()
In[394]:=
![]()
FjxとFjyがこれらの式でわかるということは,どの程度の力が骨盤に対して圧縮力として働いているのかを知ることができるということである.
では、実際にパラメータを与えてみることにする。ここであまり体重は意味をなさない(これは後で分かる)。そこで体重に対して各重量がどの程度の割合かがわかるだけで、解いていきたい。また長さについても身長によってa,b,cなどの身体の長さに関する変数は変わりうるので、これも実際の値を入れることはあまり意味がない。そこで長さに関しては身長に対する割合で表すことにする。身長をhで表すことにする。
身長:h
a = 0.02h
b =0.08h
c = 0.12h
バーベルの重さ:W0=W (つまり体重と同じ重さのバーベル)
下半身の重量:W1 = 0.4W
In[396]:=
![]()
Out[396]=
![]()
解析的に解いて,得られた答えの中のパラメ-タに数値を実際にいれて確認をするには,ReplaceAll[](/.)を使えばよいのである.
解けた!で喜んでばかりいてはいけない。出てきた答えが何を意味するのかを考えよう。なんと脊柱起立筋(いわゆる背筋)は、体重と同じ重さのバーベル(ベーベルでなくてもよい)を持った際には、体重の10倍以上の力を発揮しているのである。
次に,脊椎に働く圧縮力についてみてみる.先ほどx方向と、y方向の力の釣り合いを式によってあらわしたが、再度それを確認してみる。
In[397]:=
![]()
Out[397]=
![]()
In[398]:=
![]()
Out[398]=
![]()
式をみれば,それぞれx方向の力とy方向の力は,FMが分かって上体の傾け角度(θ)が分かれば決まることになっている.すなわちこれらは、θの関数であるということもここからわかる。θは上体の傾け角度なのだから、傾け角度が変わると大きさが変わるということである。またFjxとFjyの合力である、Fjは図から以下のようにして求められる
In[399]:=
![]()
Out[399]=
![]()
では傾き角度θが45度の場合を考えてみよう.eqx、eqyの右辺を取り出すには次のようにすればよい。
In[400]:=
![]()
Out[400]=
![]()
In[401]:=
![]()
Out[401]=
![]()
In[402]:=
![]()
Out[402]=
![]()
圧縮力はだいたい体重の11.5倍にもなっていることが分かる.体重が60Kgの人であれば、700Kg近い圧縮力が脊椎に働いているわけである。椎間板ヘルニアになるわけがこれでわかったであろうか?
この計算には、てこの腕の長さに相当するa,b,cの長さの見積もりが少し曖昧な部分が残る。姿勢の違いによって角度θも変わるが実際にはOからの距離、a,b,cも変わるため、厳密な計算には長さのパラメータの見積もりが重要である。しかし大勢はこれで十分にわかる。
例題

問:三角関数を含む任意の式(例えばx^2-50==0であったように)を自分で用意してその式を変数xについて解け。ただし、Solve[]で解けるような式とせよ。次に同じ式をニュートン法によって解き(FindRoot[]を使う)、Solveで得られた解とFindRoot[]で得られた解の違いがどの程度の大きさかを確かめよ。十分に信頼できる精度でFindRoot[]は解を求めているのかを確認せよ。
数例の式を試してみよ。
ベクトルと行列(回転行列・座標変換・内積・外積)
回転行列と座標変換の手法を学ぶ
運動を解析する上では,得られるデータの多くはスカラーではなくベクトルである.したがってベクトルの操作を学んでおかなければならない.そこでこの章では,基本的なベクトルの操作と,その応用を学ぶことにする.
ベクトルとリスト
2次元平面上の点
まずベクトルとリストの関係から考えていこう。高校数学でベクトルは習っているかと思うが、思い出して欲しい。ベクトルとは「大きさ」と「向き(方向)」をもった量のことである。従って、教科書では2次元平面上の点の位置を、原点から見た「距離 r」と「角度 θ」で表したり、あるいは、原点からのX方向の距離とY方向の距離であらわしていたと思う。(r, θ)、(x,y)といった具合に教科書に書かれていたはずである。
()括弧を{}括弧に変えてやればMathematicaでは、これをリストとして扱えるわけである。Mathematicaの柔軟な仕組みのおかげで、2次元空間上の位置,3次元空間上の位置は、{x,y}や{x,y,z}の形でリストとして表すことが可能である。リストの演算の約束を確認すればリストの演算が空間座標の位置を示す計算に対してそのまま用いることができることに気がつくはずである。
たとえば、点AAが2次元平面上で、(1,1)にあるものとする。これをベクトル、すなわちMathematicaの表現でリストで表すと
In[403]:=
![]()
Out[403]=
![]()
2次元平面上の点を描くと次のようになる。もちろんListPlot[]を使わなくても、Point[]でも点は描ける。
In[404]:=
![]()
原点{0,0}からAまでにArrow(矢印)を描く
In[408]:=
![]()
同時に描画する
In[409]:=
![]()
Out[409]=
このように表せる。
ベクトルの定数倍(スカラー倍)
次にリストの演算の約束に従うと,リストに定数倍をすれば、
In[410]:=
![]()
Out[410]=
![]()
X,Yのそれぞれの要素が定数倍される.これを図で表すと,以下のようになる.
In[411]:=
![]()
Out[413]=
図から、ベクトルの定数倍はベクトルの向きは変わらずに矢印の大きさが変わることだということがわかる。次に負の定数倍だとどうなるかと言うと,
In[414]:=
![]()
Out[414]=
![]()
In[415]:=
![]()
Out[417]=
図でみると分かるように,負の定数倍をすると「向き(方向)」が逆になる。
ベクトルの和と差
リストとリストの足し算,引き算を思い出し欲しい。この場合は、リストの長さが同じでないといけなかったはずである。
In[418]:=
![]()
Out[418]=
![]()
In[419]:=
![]()
![]()
Out[419]=
![]()
AA + {2,2}
この演算は何を意味するのだろうか?座標面でのベクトルの動きを見てみよう。
In[426]:=

Out[431]=
図でわかるように、2次元座標をリストで表した場合、リスト同士の足し算は、要素ごとの足し算であるためその要素ごとの移動を表す。この場合の要素とは、X方向、Y方向への移動距離のことになる。X方向、Y方向と向きが決められているため正の値を足すときには、X方向では右向きに移動を行い、Y方向では上向きに移動を行うことになる。逆に負の値を足す場合には、X方向左向き、Y方向下向きにベクトルが移動することになる。このようにベクトルをリストで表すとその、大きさを変える(定数倍する)、向きを変えるという操作は、リストの計算によって表すことが出来るので大変便利である。つまり座標をその座標系のなかで移動させるにはベクトルに別のベクトルを加える操作で実現可能である、ということである。
行列とリスト
行列とリスト
次は行列の扱い方とその操作である.そして,行列を使った回転移動について話を進めていきたい。すでに述べたようにベクトルは、Mathematicaのなかではリストとして表すことができた。行列も同様にリストを使って表すことが可能である。
たとえば、次のような行列があるとする。
x = ![]()
Mathematicaでは以下のように表せる。
In[432]:=
![]()
Out[432]=
![]()
そうだ,2重リストである。これが行列(Matrix)であることを確認してみよう。
In[433]:=
![]()
Out[433]//MatrixForm=
![]()
行列ですか? と尋ねる関数が用意されているのでこれを使って,行列かどうかを確認してみる
In[434]:=
![]()
Out[434]=
![]()
当然だが3×3の行列は以下のように書くことが出来る。
In[435]:=
![]()
Out[435]=
![]()
In[436]:=
![]()
Out[436]//MatrixForm=
![]()
In[437]:=
![]()
Out[437]=
![]()
ちなみに、行列の行と列は、
yの一行目は、{1,2,3} 、二行目は{4,5,6}、三行目は{7,8,9}
yの一列目は、{1,4,7}、二列目は{2,5,8}、三列目は{3,6,9}
である。
行列の演算
行列の定数倍
ベクトルのときと同様,行列の演算についても考えてみる。まずは行列の定数倍はベクトルのときと同様に表すことが出来る。
In[438]:=
![]()
Out[438]//MatrixForm=
![]()
行列を定数倍すると,それぞれの要素が定数倍される,ということが確認できる。
行列の和と差
次は、行列の和と差についてである。
In[439]:=
![]()
Out[439]=
![]()
In[440]:=
![]()
Out[440]//MatrixForm=
![]()
同じ,行数・列数の行列同士の和と差は,それぞれの要素後との和と差に等しい,ということが確認できる。それでは要素数が異なる行列同士の演算はどうだろうか?
In[441]:=
![]()
![]()
Out[441]//MatrixForm=
![]()
ベクトルのときと同じように,要素数が異なると当然のことながら演算はできない。ここまでの流れで明らかなように、リストはベクトルも行列も表すことが出来る。
行列の積
行列同士の積についてはルールがあるので覚えておく必要がる。行列同士の積を計算するには、ピリオド(ドット)を用いる。以下のシンボル同士の演算を見ればその計算方法がわかるはずである。
In[442]:=

Out[446]//MatrixForm=
![]()
Out[447]//MatrixForm=
![]()
In[448]:=
![]()
Out[448]=
![]()
行列形式によって見やすくすると以下のようになる。
In[449]:=
![]()
Out[449]//MatrixForm=
![]()
従って計算結果である行列の
1行1列目は、x3の1行1列×x4の1行1列目+x3の1行2列目×x4の2行1列目
1行2列目は、x3の1行1列×x4の1行2列目+x3の1行2列目×x4の2行2列目
2行1列目は、x3の2行1列×x4の1行1列目+x3の2行2列目×x4の2行1列目
2行2列目は、x3の2行1列×x4の1行2列目+x3の2行2列目×x4の2行2列目
という順序で計算が行われていることがわかる。
行列とベクトルの積
行列とベクトルの積についても,ピリオド(ドット)が使える。これを使うと1次方程式を行列形式の書式でかくことができ、すっきりとまとまる。
鶴亀算を覚えているだろうか?あれを行列とベクトルの形で表してみると次のようになる。
例題:鶴と亀があわせて10匹(羽?)いる。足の数を数えてみると34本ある。鶴、亀がそれぞれ何羽、何匹いるかをMathematicaで解け。鶴が片足で眠っているなんてのはなし。
In[450]:=
![]()
Out[450]//MatrixForm=
![]()
In[451]:=
![]()
Out[451]=
![]()
In[452]:=
![]()
Out[452]=
![]()
行列に関する関数たち
行列と行列式に関する話題をここでは深く説明しないが,行列に関しては以下のような関数群が用意されている。今後、Mathematicaを使って行列計算を行いたい場合にはきっと出会うことになるだろう。
転置行列
行列の「行」と「列」を入れ替えることを転置(Transpose)するという。行列の転置を求めるには関数、Transpose[]を用いる
In[453]:=
![]()
Out[453]=
![]()
In[454]:=
![]()
Out[454]//MatrixForm=
![]()
逆行列
In[455]:=
![]()
Out[455]=
![]()
In[456]:=
![]()
Out[456]//MatrixForm=
![]()
In[457]:=
![]()
Out[457]=
![]()
In[458]:=
![]()
Out[458]//MatrixForm=
![]()
行列式
行列式を求めるには,Det[]を用いる.
In[459]:=
![]()
Out[459]=
![]()
In[460]:=
![]()
Out[460]=
![]()
行列のべき乗
行列のべき乗を計算するには,MatrixPower[]を用いる
In[461]:=
![]()
Out[461]=
![]()
行列の固有値・固有ベクトル
正方行列の固有値を求めるには,Eigenvalues[]を用いる.
固有値・固有ベクトルは
n次の正方行列A,0でないベクトルxがあるとき,A x = λ x が成り立つ(x≠0)とき.λをAの固有値,xをAの固有ベクトルという.
固有値は,| A ―λ I | = 0 の根となる(Iは単位行列).
固有値の計算には,Eigenvalues[ ]を使う
In[462]:=
![]()
Out[462]=
![]()
In[463]:=
![]()
Out[463]=
![]()
行列の固有ベクトルを求めるには,Eigenvectors[]を用いる
In[464]:=
![]()
Out[464]=
![]()
In[465]:=
![]()
Out[465]=
![]()
図形の平行移動
ベクトルを使った座標の平行移動
本章の最初で、ベクトルで表現される2次元座標平面上の点の移動が、リストの演算で表されることがわかっただろう。それではそれを利用して図形の平行移動に挑戦してみよう。図形が平行移動する、ということはすなわち図形を形作る点が全て同じ移動を行うということである。2次元座標平面上に,いくつもの点が存在していてこれらが,何かの形を表しているものとしよう。たとえばただの四角形でもよいので、適当な4点を決めておこう。そして全部をつないで描画してみよう
In[466]:=
全部の点をつないで描画するには,次のように考えればよい。
(1)基本は隣の点とグラフィックスプリミティブ、Line[]で線を引く
(2)次々に、これを繰り返す
(3)最後の点だけは最初の点と結んで線を引く
一見するとFor文などの繰り返しを使わないとうまくいかないように思えるが実はすでに習ったMap[]を用いるとこれが可能だ。
In[472]:=
![]()
Out[473]=
少し脱線するが,上の式でどうして任意の点の座標が全てLine[]で結ぶことが出来るのかを説明しておこう。まずは上の式のなかで、Graphicsオブジェクトを作る前段階までが最も重要な部分なので、これだけを抜き出してくる。
In[474]:=
![]()
Out[474]=
![]()
これをみると確かに、1番目の点と2番目の点、2番目の点と3番目の点、……、というふうに次々に隣り合う点を結ぶ線分を描いている。さらに分解してみる。
In[475]:=
![]()
Out[475]=
![]()
隣あう点同士を2重リストにする,ところまでが完成している。さらに分解してみる。
In[476]:=
![]()
Out[476]=
![]()
最初の方は,p1からp4までのりスト,後ろはそれがひとつずれた(RotateLeft)リストになっている.
In[477]:=
![]()
Out[477]=
![]()
一連の操作の要点は,RotateLeft[]でリストを左に一つだけ,ずらした後,それを元の座標データと一緒に2重リストにする。その後Transpose[]することで隣り合う座標データの組にする。そしてそれをそれぞれLine[]で描画する。という過程をとっている。分かっただろうか?
さて、次に2次元座標上の任意の点を任意の移動距離だけ動かす関数をつくろう。
In[481]:=
![]()
座標{1,1}をx方向に2,y方向に2移動させると次のような位置に移動する。
In[482]:=
![]()
Out[482]=
![]()
この関数を,もとのデータである、p1からp4までに適用して平行移動させればよいので、Mapを使って各要素にこの関数を適用する。たとえばX方向に+2、Y方向に+1だけ平行移動させるには、
In[483]:=
![]()
Out[483]=
![]()
Mapを使うことでいっぺんに全部の点を同じ移動距離だけ移動させることが出来た。これを図で確認してみよう。
In[484]:=
![]()
Out[485]=
確かに,四角形全体が平行移動していることがわかる。
図形の回転移動
原点回りの回転
原点O{0,0}を中心にして,ある任意の点pを、任意の角度を回転させることを考えよう。
In[486]:=

Out[489]=
![]()
点pのx座標,y座標は半径rが1であることから,三角関数を用いることで、
px = r Cos[theta]
py = r Sin[theta]
として求めることが出来る。これは高校数学までで多くの人が習ったことだろう。
In[490]:=

Out[493]=
pを今ある位置から原点Oまわりに、角度βだけ回転(反時計回り)させて新たに、P={PX,PY}の座標を作ることにする。
このとき、もとの座標 p={px,py}から、新しい座標 P={PX,PY}を求める公式は以下のようになる。![]()
これを行列とベクトルとの積で書き表すと次のようになる。
{{Cos[beta],-Sin[beta]},{Sin[beta],Cos[beta]}}.{x,y}
回転させたい角度をβとおき、任意の座標を任意の角度だけ回転させるため、関数をつくっておくことにする。
In[495]:=
![]()
座標{1,1}を、90度回転させてみよう
In[497]:=
![]()
Out[497]=
![]()
In[498]:=
![]()
Out[498]=
![]()
図で見ると,上の計算結果を確認できることだろう
In[499]:=

Out[504]=
確かに,もとのベクトルを90度反時計回りに回転させた座標が得られていることがわかる。
このように空間座標を回転させるための行列のことを回転行列とよぶ。2重リストで表された回転行列を行列らしく表示するには、前にも出てきたMatrixForm[]という関数を用いる。
In[505]:=
![]()
Out[505]//MatrixForm=
![]()
例題
問 : 次の座標を結んで四角形をつくり、グラフィックスで表示せよ。
(1)次にこの図形(全座標)を、X方向に3、Y方向に2だけ移動させよ(すでに先ほどやったばかりです)
(2)(1)の後に,この図形(全座標)を全て原点まわりに,60度回転させよ.そして回転後の図形を、前の図形と比較できるように同じグラフ上に描画せよ。グラフは縦横比が正しく1対1になるように、AspectRatio->Automaticとして指定せよ。
In[506]:=
任意の点まわりの回転
ベクトルの回転
任意の点まわりにベクトルを回転させるには次のパッケージを読み込むのが便利である。実はここまでで説明してきた内容を網羅する関数が用意されている。
ベクトル{1,0}を原点O{0,0}を中心にしてシータだけ回転させる
In[524]:=
![]()
Out[524]=
![]()
In[525]:=
![]()
Out[525]=
![]()
{px,py,pz}について、x軸まわりの回転でシータだけ回転させる。
In[521]:=
![]()
Out[521]=
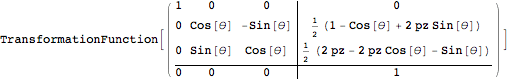
例題
問:2次元平面内(机の上に腕を伸ばしているような状態)に次の位置に肩、肘、手首の関節があるとき、肘関節の角度は何度(ラジアンではなく)であるか?その時系列変化をListPlot[]で表示せよ。元データの座標は{x,y}のならびになっているとみなせ。
肩:変数 shoulder
肘:変数 elbow
手首:変数 wrist
グラフを使って回答を行う際には、そのグラフが何を示すグラフであるのか?各軸は何を示していてその単位は何か?またいくつかのラインが同グラフ上に描かれているときには各ラインが何を示していたのか、といった補助情報が必ず必要である。
data
In[526]:=
![]()
Out[526]=
![]()
In[527]:=
![]()
ベクトルの内積
内積の計算方法
次はベクトル同士の積はどうなるのか,ということを考えよう。ベクトル同士の積には2とおりのものがある。それは「内積」と「外積」である。内積はすでに高校数学でならっていることだと思うが、これをMathematicaを使って再確認してみよう。内積の定義を今一度思い出してみよう。ベクトル aとベクトルbの間をなす角をθとおくと、そのベクトル同士の内積は次の式によって表すことができる。
![]()
これを確認してみよう。仮に a = {![]() ,0} , b = {
,0} , b = {![]() ,
, ![]() }とおこう
}とおこう
In[528]:=
次の図で分かるように,この点はおなじみの直角三角形で2つのベクトルのなす角は60度である。これをラジアン表記で表すと、Pi/3となる。
In[530]:=
Out[530]=
上記の内積を説明した式の左辺の形式をMathematicaで表すには、ドットプロダクトを用いる。すなわち「ドット(ピリオド)」を用いる。
In[531]:=
![]()
Out[531]=
![]()
右辺を計算してみよう。
ベクトルaの絶対値は、ベクトルの長さを意味するので関数の説明のところで出てきた、Distance[]を用いて計算してみる
In[532]:=
![]()
In[533]:=
![]()
Out[533]=
![]()
In[534]:=
![]()
Out[534]=
![]()
ところで、Cos[] やSin[]のような三角関数の引数としてはラジアン表記の角度を渡す必要がある。Pi/3と入力してもよいが、ラジアン標記ではピンとこない人もいるだろう。ここで度数表記とラジアン表記の変換を覚えておこう。度数を表すには定数Degreeを使って次のようにする。60とDegreeの間には空白がある。つまり60と定数Degreeを掛けている。度数からラジアンへの変換は「Degreeを掛ける」と覚えよう。
In[535]:=
![]()
Out[535]=
![]()
In[536]:=
![]()
Out[536]=
![]()
逆にラジアンから度数に変更するには逆の手順をとればよい。たとえばPi/3ラジアン(=60度)を度数に変換するには、「Degree で割って実数にする」
In[537]:=
![]()
Out[537]=
![]()
実数扱いにしない場合には、ちょっとへんな結果が返ってくる。正しい値なのでこれでもよいが度数で分かりにくい場合には、N[]を適用してやる必要がある。
In[538]:=
![]()
Out[538]=
![]()
あるいは、「180を掛けてPiで割る」と覚えよう。
In[539]:=
![]()
Out[539]=
![]()
In[540]:=
![]()
Out[540]=
![]()
左辺と右辺が同じことが明らかになった。左辺、右辺ともに、「ベクトル」ではなく「スカラー」となっていることに注意しよう。「スカラー」とは大きさだけをもっていて、方向を持たない量のことである。ベクトルとベクトルの内積の結果得られるのはスカラーであり、これは余弦関数(Cos)の性質上、\:ff0d1から+1の間の値をとる。実はベクトルの内積とは、あるベクトルが、他方のベクトルに対して投影したときにどの程度一致するのかを示している。このことは実験データや統計データの場合においては、データ間の相関係数として表現される。相関係数も同様に\:ff0d1から+1の間の値をとる。左辺の計算方式(ドット積)、右辺の計算方法(絶対値と、余弦関数を使う)のいずれを用いてもよいのだが簡便のためには、左辺方式(ピリオドによる計算)を使うことにしよう。
内積の力学への応用(仕事を例に)
ここでベクトルの内積の力学的な意味を考えておこう。内積はベクトル![]() とベクトル
とベクトル![]() によって決定されるスカラー量であるが、これは力学の世界では仕事を考える際に使われる。「仕事」の定義を確認しておこう。物体に力が加えられた際に、その力と物体の移動した距離の積を仕事と呼ぶ。
によって決定されるスカラー量であるが、これは力学の世界では仕事を考える際に使われる。「仕事」の定義を確認しておこう。物体に力が加えられた際に、その力と物体の移動した距離の積を仕事と呼ぶ。
仕事=力×移動距離
これが仕事の定義である。ここで力は大きさと方向をもつベクトルである。移動した距離はその力の向きに移動した際にこの距離をもって仕事の計算に用いる。したがって次のような例の場合には引っ張り力と物体の進む方向は異なるが、引っ張った力の移動方向に対する投影(射影)が実際に物体に対して作用した仕事になる。下の図は次のような状況を示しているといえる。すなわち床においた物体に縄をかけて右方向に引っ張ろうとしているとする。その際実際に物体に作用する力は図の青いラインで描かれた方向であるが、実際に移動するのは床面に沿っているため、その床の面(X軸)に平行な成分しか力は有効に活用されない。つまり力ベクトルの、床面への投影が実際に物体に及ぼした仕事を計算する上では必要になる。このとき上方向にも力を発揮しているにもかかわらず、上下方向には物体は動くことはないので仕事は「0」である。
In[541]:=

Out[541]=
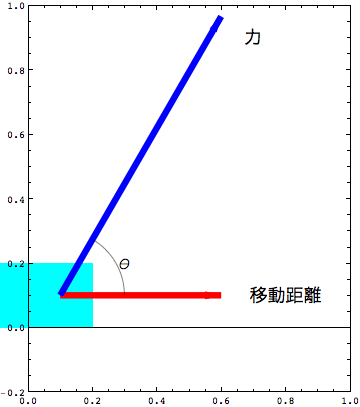

ベクトル間の角度
ところで統計の教科書には出てくる話ではあるのだが、内積の計算によって得られるのは2つのベクトルの一致度ともいうべき値である。ここで2つのベクトルが与えられた際にその2つのベクトルがなす角を求めることにしよう。これは頻繁に起こる応用問題である。具体的には運動している人の関節座標が、手首、肘、肩と3点与えられたときに手首\:ff0d肘を結ぶ前腕と肘\:ff0d肩を結ぶ上腕のなす角度、つまり肘の角度が何度だったのか?という場合などがそれにあたる。内積の定義を今一度確認すれば、2つのベクトル間の角度を導き出すことは簡単である。![]()
cos θ = 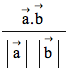
θ = ![]()
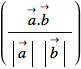
cosの右肩にマイナス1がかかっているのは、Cos[]の逆関数という意味である。逆余弦関数である。これはArcCos[]という関数が用意されている。このArcCos[]を使って、2つのベクトル間の角度を求める関数をつくると次のようになる。上の例で出てきたベクトルa、ベクトルbについてはその始点と終点をそれぞれ引数を与えることにして計算する。
In[543]:=
![]()
では先程のベクトルを使って間をなす角が確かに60度(Pi / 3)得られるかどうかを確認しておこう
In[544]:=
![]()
Out[544]=
![]()
おなじことをしてくれる関数は、そのままの名前で、
VectorAngle[]というものがある
In[545]:=
![]()
Out[545]=
![]()
ベクトルの外積
外積の定義
次に採り上げるのはベクトルの外積である。外積とはなんだろうか。ベクトルの外積は次の式によって表される。![]()
左辺をみると、ドット積ではなく、掛け算と同じ×が積の意味で使われている。図を使って外積を理解しよう。次の図は外積を説明しているが、あるベクトルaとbとの外積を計算するにはベクトルaをベクトルbに重ねるために右ねじの方向に回転させてやる。左の図ではベクトルaをベクトルbに右ねじの方向(時計回り)に回転させて重ねている。したがってこの場合は、![]() である。そして、結果として得られるものは内積の場合と異なり、ベクトルである。そのベクトルはもとの2つのベクトル(aとb)の双方に直角である。またこの定義の場合には角度θは、θ = 0 ≤θ≤π である。
である。そして、結果として得られるものは内積の場合と異なり、ベクトルである。そのベクトルはもとの2つのベクトル(aとb)の双方に直角である。またこの定義の場合には角度θは、θ = 0 ≤θ≤π である。
逆に右の図はベクトルbを右ねじの方向に回転させてベクトルaに重ねている。したがってこの場合には得られるベクトルは左の図とは逆方向になる。つまり外積は順序が重要であり、逆に掛けた答えは異なる。そして図からわかるように、外積を考えるには3次元空間を必要とする。したがってもとのベクトルa、ベクトルbのそれぞれも3次元ベクトルとして考えておく必要がある。2次元ベクトルを3次元ベクトルとして考える、というのはたとえばz軸方向の値が0である、という風においてよいということである。
Mathematicaで外積を計算するのは、Cross[]を用いる。ベクトルa、ベクトルbのそれぞれのz軸成分が0であるベクトルを次のように定める。この2つのベクトルの外積を求めるには
![]()
![]()
![]()
得られた外積はベクトルであることに気がついただろうか.また得られたベクトルのx軸成分(第1成分),y軸成分(第2成分)がそれぞれ0であることを確認しよう。つまりもとの2つのベクトルに対して直角であることもここから分かる。
外積の力学への応用(モーメント)
外積の計算は力学の世界ではモーメントの計算において行う計算そのものである。
力Fが,P点に働いているとする.rを原点からP点までの距離とすれば,O点からFに対する垂線を下ろすと,それはr sinθ となる.FかO点まわりに「アーム(例えば字ひじから先の前腕)」を回そうとする効果をモーメントと呼ぶが,これはすなわち,F × |r| sin θ となる.これは外積にほかならない.図では表示されていないが,紙面に直交する方向にはたらくベクトルである.
ベクトルを使った身体重心の計算
「重心」という言葉を耳にしたことはあるだろう。「重心」を低く、「重心」が安定している、などなどスポーツの世界では教えとして叩き込まれた人もいるかもしれない。ではいったい重心とはなんであろうか?明確に答えられるだろうか?物理の世界では重心とは明快な回答が得られるが、先にで学んだベクトルを活かして本節はこの重心をテーマにしたい。
直感的理解
定規を使って
物理的な意味での重心とは直感的には以下の実験で理解される。定規を用意しよう。定規の両端の下を人さし指で支えて、静かに両方の指を中心に向けて動かす。徐々に動かしていくとちょうど定規が水平に保たれたまま、両手の指が中心で止まる。ここが定規の中心、すなわち重心である。

ところで、もしも定規の製造工程がずさんで、その密度が均一ではなかったとしたらどうだろうか?指は中心ではないところでとどまるだろう。
やじろべえ、シーソー、モビール
均一に質量が分布していない場合はどうなるだろうか?今度は、やじろべえ、シーソー、モビールといった子供の頃に遊んだことがあるだろうおもちゃを使って考えてみよう。次の図は釣り合いが取れている場合には、支点からおもりまでの距離が等しい。1対1の距離となる。
右のおもりが倍の重さになると?
上のように、釣り合いの取れるところまで支点を動かすと、腕の長さは2対1になるだろう。これは直感的に分かるだろう。小学校ではこれを、
左のおもり×左の腕の長さ=右のおもり×右の腕の長さ
と式で表して、これが等しくなるように腕の長さ、あるいはおもりの重さを調節すれば釣り合うということを学んだ。重りとシーソー自身が一体であると考えると支点の位置が「重心」ということになる。質量分布が均一でない定規を持ってきた場合にも、その支点から見て左側、右側の重さ×腕の長さの積は等しい。このような点が重心である。つまり、重心で物体を支えるならばその物体は回転を起こさずに姿勢を保ったままで保持できるのである。すなわち、その点で物体全体の質量を支えているのと同じことであるといえる。
重心の定義
記述的定義
地球上のあらゆる物体はその物体を構成する全ての部分(分子、原子)について地球の中心に向かう重力の作用を受けている。重力は力の方向がいずれも平行で同じ向きに働いているとみなしても差し支えない。このように平行に働く力はこれを一点に合成することが可能である。この合成点は物体の位置にかかわらずに剛体(*)では常に同一の点を示す。この点のことを重心または質量中心と呼ぶ。このように、重心というのは地球上の重力場における物体について、その物体に働く力の合成点として導入された、力学上考え出された仮想の点のことである。従って、その重心が物体内に存在しないこともありうる。重心はその物体に働く重力の合力の作用点であるというだけではなく、その物体が運動をするときの代表点としても重要な意味をもっている。
* 剛体:質量不変であり大きさが全く変化しない物体のことを指す。固いものという意味ではない。
数学的定義
![]()
やじろべえの数学的な記述
やじろべえ(シーソー)の腕の長さと重りの積は等しいということであったが、これはすなわち重心回りの回転モーメントが釣り合っているということを表している。回転モーメントとは重心から離れたところに力が作用するとその物体を回転させようとする力が働くことになるが、この物体を回転させようとする力のことを回転モーメント(単にモーメント)と呼ぶ。反時計回りの回転を正で表し、時計回りの回転を負で表すと
+10Kgf × 2 +(−20Kgf)×1 = 0
となり、釣り合っていることを証明できる。0というのは重心回りの回転モーメントが0であり、回転についての釣り合いが取れていて水平を保つことを意味している。
ベクトルの内分
内分点
高校数学の「代数・幾何」では位置ベクトルの内分点を求めるための式が出てきた
問:線分ABをm:nの比に内分する点をPとして、点A, B, Pの位置ベクトルをそれぞれ、![]() ,
, ![]() ,
,![]() とすると、
とすると、![]() =
=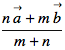
である。
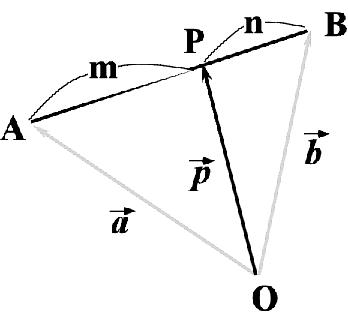
証明すると![]() =
= ![]() =
= 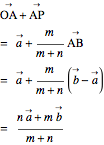
このベクトルの内分点が理解できれば、これから先の身体重心を定義した式を容易に理解できるだろう
例題 : 写真から重心を求める
サンプル画像の読み込み
さて、それではようやく身体の重心を突き止めることにとりかかろう。本当は人間の「裸」の写真、あるいは水着での写真があればベストだが、ちょっと用意することが出来なかったため、人形を使って説明することにする。
![]()
![]()

![]()
これを人間にみたてよう。
合成重心の算出(ベクトルの内分を使って)
考え方はこうである。まず身体各部、すなわち頭部、胴体部、上腕部などのセグメントごとに重心位置を求める。これらの重心位置をもとにして隣り合うセグメントの合成重心を求めていく。これを繰り返すことにより、身体全体の重心位置を求めるというものである。
まずAの重心位置とBの重心位置を求め、その内分点であるDをもとめ、さらにDとCの重心とを合成して3つのセグメントの合成重心位置(![]() )を算出するということを上の図は示している。同じような密度であれば上の図ではAよりもBの方が大きいので当然Bのセグメントの方が質量が大きい。つまり合成重心位置はBにより近い位置にくる。従って、さきのやじろべえ(シーソー)のときのようにこの合成重心位置を支えることでAとBの双方を回転させずに保持できる。しかしながら、図をみると気がつくと思うがAとBの角度が少づつ広がると合成重心位置はAとBのどちらにも存在せずに双方のセグメントの外に出てしまう。つまり重心は仮想の点であるので、セグメント内に存在しないこともあるわけである。
)を算出するということを上の図は示している。同じような密度であれば上の図ではAよりもBの方が大きいので当然Bのセグメントの方が質量が大きい。つまり合成重心位置はBにより近い位置にくる。従って、さきのやじろべえ(シーソー)のときのようにこの合成重心位置を支えることでAとBの双方を回転させずに保持できる。しかしながら、図をみると気がつくと思うがAとBの角度が少づつ広がると合成重心位置はAとBのどちらにも存在せずに双方のセグメントの外に出てしまう。つまり重心は仮想の点であるので、セグメント内に存在しないこともあるわけである。
最初に重心の定義を式で示したように各身体セグメントの質量と各身体セグメントの部分重心位置のみがわかれば一気に計算が可能である。
![]()
そこで必要になるのが、身体各部分の質量分布(mi)を計算する式および各セグメントのどの位置に重心位置があるのか(xi)を推定する式である。
Chandler.m
Note
身体重心を計算するために先人はものすごい苦労をしてきた。Chandllerは死体を切り刻んで各セグメントの質量比(体重に対する)、質量分布(重心位置)、慣性モーメントを実測した。この実験値をもとにして身長および体重から身体各部の、質量比、重心位置、慣性モーメントを推定する式を導出した。これを仰木はMathematicaを使ってPackage化して、誰でもすぐに使えるようにした。BeginPackage[]以下を評価(Shift+Enter)して欲しい
Package
(* Yuji Ohgi Last Modified 1996/12/7 *)
(* Reference from "Investigation of Inertial Properties of the Human Body",Chandller,R.F.,et al,March 1975 *)
(* You can get some useful parameters by this packeges,for example;
1)Segment weight.
2)Center of Gravity(CG) of each segment.
3)Moment of Inertia of each segment about it's segment CG.
4)Center of Gravity(CG) of total human body
*)
(* You must use these modules with SI units.Total Body Weight=[Kg]; Segment Length=[m]; *)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
質量分布
上で評価したパッケージは、
(1)身体各部の部分質量
(2)身体各部の部分重心位置
(3)身体各部の慣性モーメント(XYZそれぞれの軸回り)
を求めることが出来る。ここでは(1)、(2)の機能を使う。
まずは各部分の質量を求めておこう。求められるのは以下のセグメントである。
頭、胴体、右上腕、右前腕、右手、右大腿、右下腿、右足、左上腕、左前腕、左手、左大腿、左下腿、左足
私の体重は約64.5Kgである。そこでこれを人形の体重と仮定して計算してみよう。
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
全部足したら、64.5Kgになるはずだが
![]()
![]()
1g以下の精度で誤差が出ている。
セグメント関節位置とセグメント重心位置
頭の重心位置を知るには、「どこからどこまでが頭」なのかを教えてやらねばならない。
![]()
頭の場合には、頭のてっぺん(頭頂:vertex)と両方の耳の(耳下点)を結んだ中点を与える必要がある。そこで適当だが耳の位置を示し、必要とされる各関節座標を黒丸にして表示した写真をもう一枚用意した。ファイル名はpuppet1-2.JPGである。
![]()

![]()
この黒丸点の座標が分かれば、この人形の重心がわかることになる。ではこれらの座標を求めよう
画像上の座標を求める
Mathematicaには便利なデジタイズ機能が備わっている。任意のグラフィックス(自分で描いたグラフも含む)を選択し、コントロールキーを押しながらマウスクリックすると、その際の座標が記憶される。その後、コントロールキーを押したまま保持し読み取る座標をいくつかクリックしたら最後にコピーする(Ctl+C)、そしてカーソルをまだ入力していない位置に持っていき、ペースト(Ctl+V)で座標が読み取れる。図を選択した状態で図上にマウスを持っていくとウィンドウ左下にマウスの座標が示される。ためしに、頭の点をデジタイズしてみる。
![]()
![]()
耳下点は左右の耳の中点なので、左右の耳をデジタイズして、それを2等分してやればよい
![]()
![]()
![]()
![]()
![]()
そして頭の重心位置は、次のようにして求められる。
![]()
![]()
頭の重心位置を元の画像に上書きして確認してみる。
![]()
![]()

![]()
なるほど、おおよそ頭の重心位置あたりにきていそうだ。ちなみに解剖学的に「頭」とは耳の穴よりも上部分を指す。Chandllerの場合には耳の穴よりも下は実は胴体に含んでいる。では、次々に各部分の重心位置を求めてみよう。そのために、まずは各部分の関節の座標をデジタイズしなければならない。面倒なので一気にデジタイズしてしまってあとでそれを各点に割り当てよう。では最初からもう一度、つまり21点をデジタイズする。


![]()
![]()

セグメントの重心位置を求める
![]()
![]()
胴体は両耳の中点と、左右の股関節(正確には大転子)が必要だ。
![]()
![]()
![]()

![]()
残りは次々に計算していこう

足部は足首、かかと、つま先の3点の座標が必要だ。
![]()
![]()
ここまでで求めた各部分の重心を全部重ね描きしておこう
![]()

![]()
身体重心を求める
では必要なデータが出揃ったところで、身体全体の重心位置を求めよう
![]()
の式をよくみて、これをMathematicaで書き下せばよい。ちなみにy座標も同じ式で通用する。要は各セグメント質量にそのセグメント重心位置を掛けて、次々に足していき、最後に身体全部の質量(=体重)で割ってやるだけのことである。

![]()
![]()

![]()
うむ。だいたい重心の近くにあるようだ。
重心の意味
重心とは、剛体の質量がただ1点に集中して存在したとみなす点のことであり、その点でその物体の運動を記述することが出来ることを意味する点のことである。質量をもつが大きさをもたない点のことを質点と呼ぶが、重心とは運動をこの質点によって捉えようとするために考え出されたものである。