第４週：プログラミングのいろは（３）複数の命令をひとまとめに

今週は１行あるいは複数行の命令をひとまとめにすることで新しくひとつの命令として定義する方法と、そのようにして新たに定義した命令を利用する方法を学びます。これらの方法を学ぶことで、論理構造が明確な、簡潔かつ分かりやすいプログラムが書けるようになります。

4.1　プログラムに見られる論理構造
4.2　論理構造の部品化（メソッドの作成）
4.3　引数の利用とメソッドの汎用化
4.4　引数を増やしてメソッドの汎用度を上げる
4.5　メソッド間の相互参照

4.1　プログラムに見られる論理構造

今週のテーマである「複数の命令をひとまとめに」を学ぶためには、プログラムの論理構造についてきちんと理解をしておく必要があります。この話題は第２週の「コメントについて」のところで触れた「目的の階層構造」という考え方の復習にあたりますが、今週のみならず、これからプログラムを学習を進める上で非常に大事なことを含んでいます。そこで、ここではもう少し踏み込んで再学習しておきましょう。

たとえば「家を描くプログラム」を、論理構造という観点から見てみましょう。

/*　家を描く
　　作成日：00.5.3　
*/
class House01 extends Turtle{
	void start(){

		// 屋根を描く
		rt(30);	// 前処理（タートルの角度を調整する）
		int i;
		for(i=1; i<=3; i++){
			fd(100); rt(120);	// 三角形の一辺を描く
		}
		rt(60);	// 後処理（タートルの角度を調整する）
			
		// 本体を描く
		for(i=1; i<=4; i++){
			fd(100); rt(90);	// 四角形の一辺を描く
		}
	}
}

このプログラムの目的は「家を描く」ことです。この目的は、さらにそれを実現するためのより詳細な目的に分割できることが分かります。すなわちブロックコメントで示される「屋根を描く」と「本体を描く」という部分です。これらを「屋根を描く→本体を描く」という順序でプロセス化し、実行して行くことで、このプログラム全体の「家を描く」という目的が実現されます。

さらに、プロセスを構成する「屋根を描く」「本体を描く」それぞれには、それらを実現するためのさらに詳細なプロセスがあります。すなわち、「屋根を描く」ならば「前処理→正三角形を描く→後処理」、「本体を描く」ならば「正方形を描く」です。

以上の分析に基づいて、「家を描く」プログラムの論理構造を図にまとめたのが以下のものです。

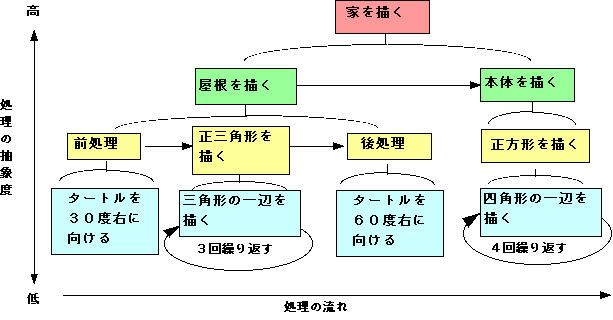
プログラムの論理構造は、目的の分割という観点からの処理の抽象度と、時間の経過という観点からの処理の流れという二つの要素から成り立っています。現在、比較的短い（そして単純な）プログラムを書いているうちはあまり実感されませんが、正しいプログラムを書くためには、この両方の要素をきちんと設計する必要があるのです。

4.2　論理構造の部品化（メソッドの作成）

これから学習を進めてゆくにつれ、より複雑な仕組みを持つプログラムを書いて行くことになります。その際、ソースコードの行数が増えて行くと、せっかく論理構造をきちんと設計しておいても、書いているうちに頭が混乱して間違ったコードを書いてしまうといったことが起こり得ます。

そこで、ある特定の目的を実現するプログラムの部分を「部品」として抜粋し、ひとまとめにして名前を付け、その名前を新しい命令として定義しプログラム中で利用することができれば非常に便利です。たとえば、家を描くプログラムの場合ならば、正三角形を描く部品と正方形を描く部品を用意します。それぞれを仮にtriangle、rectangleと名付け、プログラムの処理の流れの中で以下のように命令として利用できると、プログラムはすっきりと見やすくなります。

/*正三角形を描く部品の定義*/
triangle{
	int i;
	for(i=1; i<=3; i++){
		fd(100); rt(120);	// 三角形の一辺を描く
	}
}
 

/*正方形を描く部品の定義*/
rectangle{
	int i;
	for(i=1; i<=4; i++){
		fd(100); rt(90);	// 四角形の一辺を描く
	}
}
 

/*　家を描く
　　作成日：00.5.3
*/
class House01 extends Turtle{
	void start(){

		// 屋根を描く
		rt(30);	// 前処理（タートルの角度を調整する）
		triangle;	// 正三角形を描く		
		rt(60);	// 後処理（タートルの角度を調整する）
			
		// 本体を描く
		rectangle;	// 正方形を描く
	}
}

上の記述はまだ不完全なものですが、Javaではこのような要領で、ある一定の役割を果たす命令群を抜粋し「部品」として扱うことができます。これは、処理の抽象度のレベルが下位にある命令群（上記の場合ならば「（三角形/四角形の一辺を描く）を３/４回繰り返す」）をまとめて、その一つ上のレベルの命令（「正三角形/正方形を描く」）として利用することを意味します。そのことで、処理の抽象度のレベルが一定になるようにプログラムを書くことができ、結果的にプログラムの見通しをよくすることにつながります。

そのやり方ですが、次のように行います。まずはじめに部品の定義をする書式は次の通りです。

void 部品名(){

	・・・処理を記述・・・

}

先ほどの正三角形を描く部品triangleならば以下のようなります。

void triangle(){
	int i;
	for(i=1; i<=3; i++){
		fd(100); rt(120);	// 三角形の一辺を描く
	}
}

この定義をプログラム中に次のように書いておきます。

class House01 extends Turtle{

	/*正三角形を描く部品の定義*/
	void triangle(){
		int i;
		for(i=1; i<=3; i++){
			fd(100); rt(120);	// 三角形の一辺を描く
		}
	}

	void start(){

		・・・省略・・・

	}
}

部品の定義を書く場所は、class...で始まる｛｝内で、かつvoid start()の｛｝の外側ならば、どこでもかまいません。

つぎに、定義した部品を命令として利用する方法です。利用したい場所で、以下のような書式で呼び出します。

部品名();

たとえばtriangleを命令として利用する場合は、次のようになります。

/*　家を描く
　　作成日：00.5.3
*/
class House01 extends Turtle{

	/*正三角形を描く部品の定義*/
	void triangle(){
		int i;
		for(i=1; i<=3; i++){
			fd(100); rt(120);	// 三角形の一辺を描く
		}
	}

	void start(){

		// 屋根を描く
		rt(30);	// 前処理（タートルの角度を調整する）
		triangle();	// 正三角形を描く		
		rt(60);	// 後処理（タートルの角度を調整する）

		// 本体を描く

		・・・省略・・・

	}
}

Javaでは、このような複数の命令を集めて名前を付けたプログラムの部品のことを、特にメソッドと呼びます。部品の定義は、正しくはメソッドの定義といいます。そして、定義されたメソッドはその固有名と共に「〜メソッド」と呼ばれます。上の例で定義したtriangleは、以降triangleメソッドと呼ぶことにします。

気づいた人もいるかもしれませんが、今まで”おまじない”として扱ってきたvoid start(){ ... }も、本当のところはstartメソッドという一つのメソッドの定義の記述です。しかし、このプログラムのどこを見渡しても、

start();

というふうにstartメソッドを命令として利用する記述がありません。これはstartメソッドが、タートルグラフィックスの環境を定義するTurtleクラス（みなさんの自作のプログラムと一緒にコンパイルされるプログラム）によって利用されるメソッドだからです。今その仕組みを細かく知る必要はありませんが、最低限つぎのルールを理解しておいてください。

さらにもう一つJavaのプログラミングに関して、次のようなイメージを持てると良いでしょう。

最初にあげた事項に関しては、たとえば現在勉強しているタートルグラフィックスのプログラムの処理（つまり、タートルの画面が現れ、しかるべき図形が描かれ、、、etc.）は、いつでもみなさん自身が作成するクラス（たとえば先ほどの”House1クラス”）とTurtleクラスとの連携によって実現していることを理解して下さい。簡単にいってしまえば、ウインドウやタートルや、そのタートルに対する命令など、「タートルグラフィックス環境」そのものを提供するのがTurtleクラスの役割です。それに対してみなさん自身が作成するクラスは、その環境を用いて「何を描くか」を指示する役割を持っています。

さらにJavaでは、プログラミングを行う上でたびたび必要となるであろう、あらゆる機能を実現する”出来合のクラス”がすでにクラスライブラリに用意されています。Turtleクラスもそこに用意されるいくつかのクラスを利用することで作成されています。

そして、そういったJavaのプログラムを構成するあらゆるクラスが、今週学習する”メソッド”によって構成されるものであることも知っておいてください。

練習問題　4-1

正方形を描くrectangleメソッドも作成し、上記の家を描くプログラムを完成せよ（House01.java）

4.3　引数の利用とメソッドの汎用化

先ほどは正三角形、正方形それぞれを描くメソッドを一つずつ作成しました。しかしもしも「正n角形を描くメソッド」というものが定義できて、呼び出して利用する時にnの値をその都度与えることができれば、プログラムはもっと短くなりますね。

たとえばこの正n角形メソッドの名前をpolygonとして、startメソッドの中で以下のように利用することを考えます。

void start(){

	// 屋根を描く
	rt(30);	// 前処理（タートルの角度を調整する）
	polygon(3);	// 正三角形を描く		
	rt(60);	// 後処理（タートルの角度を調整する）

	// 本体を描く

	polygon(4);	// 正方形を描く

}

正三角形や正方形を描くといった具体的な機能から、正n角形を描くという抽象的な機能へとメソッドの定義をし直すことで、そのメソッドの汎用性が上がり、より便利なものになる場合があります。メソッドの機能が、個別的・具体的な対象を持つことによる束縛から解放されるからです。そういった意味で、メソッド機能の抽象度を上げることは汎用度を上げることにつながるのです（やりすぎると、なんだか分からないメソッドができてしまいますが）。今回のケースでは先に示したとおり、メソッドを呼び出す際に一緒にデータ（値）を与えるような方式をとることで、抽象度・汎用度を上げるやり方を学びます。

まずはじめに、正n角形を描く処理の中身を考えましょう。正三角形を描く場合と正方形を描く場合の双方の共通点をピックアップして、どのようにすればよいのかを考えます。

// 正三角形を描く処理
int i;
for(i=1; i<=3; i++){
	fd(100); rt(120);	// 三角形の一辺を描く
}
 

// 正方形を描く処理
int i;
for(i=1; i<=4; i++){
	fd(100); rt(90);	// 正方形の一辺を描く
}

ちょっとした算数の問題ですね。これだけで分かりにくければ、正五角形や正六角形などを描くケースも考えて、共通点を見いだして下さい。

結論からいうと、正n角形の描画には次のような法則性があります。仮に長さは一辺１００、角数はnとして、

これが分かれば処理の内容を書くことができます。今の時点で学習済みの知識を動員すると、正n角形の図形を描くpolygonメソッドの定義は、

// 正n角形を描くメソッドの定義
void polygon(){

	int angle;
	angle = 360/n;	// 回転角度を割り出す

	int i;
	for(i=1; i<=n; i++){
		fd(100); rt(angle);	// 正n角形の一辺を描く
	}
}

となるはずです。

しかしこのままでは赤字で示した角数を表す変数nの、その都度の実際の値を受け取る仕組みがどこにもありません。メソッドの外部から何らかの値を受け取りたい場合は、それを受け取るための変数の利用をメソッド名の直後にある（）内で宣言します。たとえばpolygonメソッドならば描く図形の角数を記憶する変数nを、次のように宣言してメソッドの定義を行います。

// 正n角形を描くメソッドの定義
void polygon(int n){

	int angle;
	angle = 360/n;	// 回転角度を割り出す

	int i;
	for(i=1; i<=n; i++){
		fd(100); rt(angle);	// 正n角形の一辺を描く
	}
}

このようにしておくと、int型のデータを一つだけ外部から受け取ることができます。最初に示したとおり、startメソッドの中で、

polygon(3); // 正三角形を描く
 

polygon(4); // 正方形を描く

と呼び出すことで、polygonメソッドに値を渡し、描画を実行させることができます。

プログラミングの世界では、呼び出した際にメソッドに渡す値（polygonの例では３や４といった値）のことを特に引数（あるいは実引数）、メソッドの定義の際に外部から値を受け取る準備として（）内に宣言する変数（polygonの例ではint n）のことを特に仮引数、と呼ぶことがあります。

練習問題　4-２

polygonメソッドを実際に作成し、それを用いて家を描くプログラムを完成しなさい（House02.java）。

4.4　引数を増やしてメソッドの汎用度を上げる

メソッドを定義する際、引数を二つ以上とるようにすることができます。たとえば先ほどのpolygonメソッドは、そのままでは必ず一辺１００で図形を描くようになっています。それを、一辺の長さも引数で指定できるようにして、任意の長さの図形を描くように改造できれば、より汎用性が上がります。

引数を二つ以上とるようにするためには、メソッドの定義の際に複数の仮引数を宣言します。polygonメソッドの場合、長さを表す変数sizeを次のように宣言して、長さの指定に対応できるよう準備します。

void polygon(int n, int size){

書式は、カンマ（,）で区切って並べるだけです。このメソッドを利用する際には、仮引数として宣言されている順にやはりカンマで区切りながら実引数を与えます。たとえば長さ５０の正８角形を描く場合なら、

polygon(8, 50);

という風に実引数を与えます。

もちろん、それに伴いpolygonの定義の中にある処理も、実数１００ではなく変数sizeを利用するように書き換えておかなければなりません。

練習問題　4-3

polygonメソッドを長さの指定ができるように書き換た上で、それを用いて一辺５０の家を描くプログラムを作成しなさい（House03.java）。

4.5　メソッド間の相互参照

あらかじめ定義した自作メソッドを利用して、新たな自作メソッドを定義することもできます。以下の例ではpolygonメソッドと、polygonメソッドを利用して家を描くhouseメソッドを定義しています。

/*　家を描く
　　作成日：00.5.3
　　備考：houseメソッド（一辺の長さを引数にとり、polygonメソッドを利用する）を使って描く
*/
class House04 extends Turtle{

	/* startメソッド：タートルに描画を実行させる */
	void start(){
		// 一辺の長さ100の家を描く
		house(100);
	}

	/* houseメソッド：一辺の長さsizeの家を描くメソッド */
	void house( int size ){

		// 屋根を描く
		・・・省略・・・
		polygon(3, size);	// 一辺の長さsizeの正三角形を描く
		・・・省略・・・			

		// 本体を描く
		polygon(4, size);	// 一辺の長さsizeの正方形を描く
	}

	/* polygonメソッド：一辺の長さsizeの正n角形を描く */	
	void polygon( int n, int size ){

		・・・省略・・・		
	
	}
}

ここで注意すべきなのは、houseメソッドとpolygonメソッドのそれぞれの定義において、同じ名前を持つ変数が使われていることです。両方とも仮引数にint sizeが宣言されています。Javaでは、ある変数が宣言される場合、その変数の有効範囲はもっとも近い直前の｛からそれに対応する｝までと決まっています。またあるメソッドの仮引数として宣言された変数の場合、有効範囲はそのメソッドの定義内のみということになっています。従って、houseメソッド、polygonメソッドそれぞれのint sizeは、全く別のものとして扱われることになります。

練習問題　4-4

上記のプログラムHouse04.javaを完成しなさい。

練習問題　4-5

次のように、徐々に小さくなって行く正方形を一定の角度ずらしながら重ねてゆき、「巻き貝」の模様を描きなさい（Makigai.java）。

ヒント　→　重ねる正方形の数は１９個。一辺の長さは１９×５から徐々に小さくなって行きます。また、ずらす角度は３６０度を２０で割った値、すなわち１８度です。

練習問題　4-6

正３角形から正１０角形までを連続して描くPolygons.javaを作成しなさい。但し正７角形は角度が割り切れず、そのままではうまく描けないので、除外するようにしなさい（もちろん繰り返し文を使うこと！）。

＞＞　目次ページへ