Home >> Lecture 3
第3回 制御文復習
3−1.変数のスコープと状態遷移
■自己参照代入文
例えば、以下の記述があるとしましょう。この代入分の羅列は、変数の値を変えていますが、 その変数が持っていた過去の値とは、まったく関係なしに、新しい値をどんどん代入してしまっています。
x = 30; x = 20; x = 10;
一方、次のように変数の過去の値を参照して、その変数の新しい値を計算することができます。
x = x +10; // xがx+10と等しいという意味ではありません
これは、今までの数学の常識から考えれば、かなりおかしな記述です。 しかしながら、Javaの代入の=というのは、数学の等価を示す=とまったく異なる働きをするのです。 =の左辺と右辺ではまったく意味が異なります。
▼代入文の=の左辺と右辺:
=の左辺:右辺の計算結果が、左辺に置かれている変数が持つ新しい値として代入されます。
=の右辺:右辺に変数が現れた場合、その変数が現在持っている値が参照されます。
このような代入文を「自己参照代入文」と呼びます。 左辺の変数に代入する場合、代入されるのと同じ名前の変数が右辺の式の中に出てきても構いません。 たとえば、次のような代入文などが考えられます。 「〜chan」はすべて整数の変数だと思ってください。
takochan = takochan * 2; //takochanの値を2倍にします。 mamachan = mamachan - 10; //mamachanの値は-10されます。 mikan = mikan + 1; //mikanの値は+1されます。 nekochan = nekochan / 2; //nekochanの値は半分になります。 ikurachan = mamachan + takochan / nekochan; //ikurachanの値はどうなってしまうのでしょう?
右側の式の方に変数が記述されている場合は、「その変数が現在もっている値」に置き換えられます。 そして、左側にある変数名に、「その変数が新しく持つ値」として、右側の式が評価された後の定数が代入されます。 ですから、「mikan = mikan + 1;」は、mikanがもつ現在の値を参照して、 その値に+1された値が、mikanが新しく持つ値として代入されます。 たとえば、mikanが20を保持していたら、21を保持することになります。 その他の例を見てみましょう。
例: i = i + 5; …変数iが保持していた値に5を足して、新しいiの値とします。 x = 10 / x; …10を変数xが今まで保持していた値で割って、新しいxの値とします。 y = ( 20 * y ) - z; …自分で考えてみなさい、、、、
実は、代入を行なう=は演算子で、しかも右結合性(Right Associative)を持っています。=の演算子の計算結果は、 左辺に代入された値を持っています。ですから、次のように複数の変数に代入する記述を行なうことも可能です。 しかし、あまりお薦めしません。プログラムが読みにくくなるからです。
x = y = z = 0; // x = ( y = ( z = 0 ) ); という意味、右から評価されていくのですべてに0が代入されます。
★自己参照代入文の省略形
なお、同一の変数に代入する代入文(これを自己参照代入文と呼びます)には、次のような省略形が用意されています。 優先順位に注意して例を見てください。
+= 例:y += 45; → y = y + 45; -= 例:z -= 5 * x; → z = z - 5 * x; *= 例:w *= x + 15; → w =w * ( x +15 ); /= 例:r /= y - 45; → r = r / ( y - 45 ); %= 例:p %= p/2; → p = p % (p/2);
演算子の順番を逆に記述した場合は、=+や、=-、エラーになりませんが、予期した自己参照代入の効果がありません。 これらは、=の後の+やーが、単なるプラスやマイナスを示す単項演算子として解釈されるからです。 更に、=*や、=/などは、コンパイラによってエラーにされてしまいます。
x=+6; // これは、単に変数xに6が代入されるだけ
★インクリメント・デクリメント演算子
自己参照代入文に関して、+= や -=といった便利な記述があると説明しましたが、 変数の持っている値に1を足したり、1を引いたりするのは、更に省略形が用意されています。 これらはインクリメント・デクリメント演算子(Increment / Decrement Operator)と呼ばれて 重宝されています。それぞれ、++と−−で表現することができます。
y = y + 1; → y += 1; → y++; z = z -1; → z -= 1; → z--;
更に、式中ではこれらの演算子を別の演算子と組み合わせて使うことができます。
8 * y++ → 8 * y, y = y + 1 z = y-- / 10; → z = y / 10; y = y - 1;
ただし、このようにしますと式を評価しているのか、代入をやっているのか、かなりわかりにくくなります。 C言語系でない他の言語のプログラマは、これを副作用(Side Effects)と呼んで、忌み嫌っていました。 そこまで嫌う必要はありませんが、あまりに頻繁に使ってしまうと自分でもわからなくなってしまうので、 使う際には注意した方がよいでしょう。
インクリメント・デクリメント演算子は、変数の前か後ろのどちらかにつけることができます。 前につけるときと、後ろに付けるのは微妙に副作用が違うので注意が必要です。
▼副作用の違い:
前につける その変数を先に更新してから評価する
後ろにつける その変数を評価した後に更新する
例えば、変数yが値30を持っていると仮定して、それぞれの場合で次のように変化します。
z = ++y * 10; → y = y + 1; z = y * 10; z = y++ * 10; → z = y * 10; y = y + 1;
両者ともyの値は31になりますが、zの値は上の方が310、下の方が300となります。
インクリメント・デクリメント演算子の副作用のまとめ
| 表記法 | 式における評価の方法 | 変数に対する効果 |
|---|---|---|
| 変数++ | 変数の元の値を評価する | 変数は+1される |
| ++変数 | 更新された後の変数の値を評価する | 変数は+1される |
| 変数-- | 変数の元の値を評価する | 変数は+1される |
| --変数 | 更新された後の変数の値を評価する | 変数は-1される |
■変数の状態遷移
プログラム中のすべての変数の値が一定である瞬間を、そのプログラムが「ある状態(state)にある」と 表現します。 プログラムの中で、変数がどんどん値を変えていくことを、プログラムの状態遷移(state transition)と 呼んでいます。
int n = 10; n = n + 1; // 状態遷移していく n *= 2; n ++;
■変数のスコープ
あるブロックの中で宣言された変数は、そのブロックの中(そのブロックが実行されている間)だけ、存在します。 ブロックを外れてしまうとその変数は、なくなってしまいます。 変数が生きている範囲を変数のスコープ(scope)と呼びます。
{
int x =25; // これ以降xが有効
{
int y =25; // これ以降はxもyも有効
}
// 内側のブロックが終わるとyは消えてしまう
}
// 外側のブロックが終わるとxも消える
3−2.主要構文
■条件式と論理式
★比較演算子
両側の式の値を評価して、2つの値の比較を行なう 演算子のことを「比較演算子(comparator)」と呼んでいます。Javaでは、比較演算子を使った条件式は次のように記述します。
▼条件式:
式 比較演算子 式
比較演算子としては、次のようなものが使えます。
| 比較演算子 | 意味 | 使用例 |
|---|---|---|
| > | 左の式が右の式より大きい | takochan > 10 |
| < | 左の式が右の式より小さい | x < y + 10 |
| >= | 左の式が右の式より大きいか等しい | takochan >= 10 |
| <= | 左の式が右の式より小さいか等しい | ikachan <= 0 |
| == | 左の式が右の式と等しい | takochan == ikachan * 2 |
| != | 左の式が右の式と等しくない | ikachan != 0 |
記号は全部半角で入力するようにしてください。しかも、記号と記号の間に空白を入れないでください。 ですから、「> =」みたいに、不等号と等号の間には空白が入ってはいけません。 それから、イコールの入った不等号は不等号の方から記述します。「>=」を「=>」と書くとコンパイラに叱られます。 同じように、「=<」もコンパイラに叱られます。また、等しいという意味のイコールは 「==」イコールを2つ書かなければならないことに注意して下さい。 Javaでは、イコール1つの「=」は、代入演算子、イコール2つの「==」は、等号演算子と明確に区別されています! 条件式も一般の式と同じように、評価されます。ただし、評価結果は論理値になります。 条件式が満足される場合は、「true」という論理値に評価されます。 また、満足されない場合は「false」という論理値に評価されます。
★論理演算子
そのために、1つの仮定文で複数の条件式を記述するために、「論理式(logical Expression)」が一般のプログラミング言語 では用意されており、もちろんJavaでも記述することができます。 記号は全部半角記号を用います。!は否定、&&は「かつ」、||は「または」を 意味します。
▼論理式:
条件式
! 論理式 // 否定を表す
論理式 && 論理式 // 論理積「かつ」を表す
論理式 || 論理式 // 論理和「または」を表す
!は、そのままでも使っても良いでしょうが、!(条件式)と丸括弧で囲った方が読みやすいでしょう。 評価の優先順位は、!が一番高く、次に&&で、最後は||です。なお、これらの演算子も左結合性なので、 ||の場合は、左側の論理式がtrueに評価された場合は、右側は評価しません。 また、&&では、左側の 論理式がfalseに評価された場合は、右側は評価しません。 それから、「または」を表す||は、縦棒2つです。 大文字のI(アイ)や小文字のl(エル)ではないので注意して下さい。縦棒は、JIS配列のキーボードでは、¥マーク キーをShiftキーを押しながら入力します。これらの論理式について、論理値を記述しておきます。 まず、単項の否定演算子は以下のようになります。
| 論理式(否定, NOT) | 評価結果 | |
|---|---|---|
| !true | → | false |
| !false | → | true |
二項の論理積、論理和演算子は以下のようになります。
| 論理式(論理積, AND) | 評価結果 | 論理式(論理和, OR) | 評価結果 | ||
|---|---|---|---|---|---|
| true && true | → | true | true || true | → | true |
| true && false | → | false | true || false | → | true |
| false && true | → | false | false || true | → | true |
| false && false | → | false | false || false | → | false |
「かつ」は両方の条件式が満足するときだけ「true」に 評価されます。「または」はどちらかの条件式だけが満足すれば「true」に評価されます。 加えて、「または」の場合、左側の条件式が「true」と評価された場合で、 右側の条件式は評価されません。 それから、「&&」と「||」はどちらが優先順位が強いかと言えば、 たいていのプログラミング言語では「かつ」の方が優先順位が強い演算子になっています。 「かつ」が「または」に勝つとでも覚えておいて下さい。 ただし「!」という否定が演算子的には一番強い結合力を持っています。 下記にいくつかの条件式の例を記述します。
month%2 == 0 && month < 8 //偶数の月の小の月の条件式 100<=x && x<=200 // 「100<=x<=200」とは書けません!注意して下さい! x==0 || x==1 //「x == 0 || 1」とは書けません!注意して下さい! !( x <100 ) && x%17 == 0 //否定には丸括弧を付けた方がわかりやすいでしょう
また、論理式も最終的には、論理値として評価されます。以下のプログラムの断片も、論理値が表示されます。
int x =25; System.out.println( x >= 100 && x <= 200 ); // falseが表示されます。
排他的論理和(exclusive or:どちらか一方だけがtrueのときだけtrueになる)は、&&と||演算子を利用して 次のようにして表現します。AとBは共に条件式(または論理式)とします。
▼排他的論理和
(A || B) && !(A && B)
☆論理式の書換え規則
以下の書換え規則はド・モルガンの法則として 有名です。論理式をPとQという形で記述します。日本語とJavaでの記述の両方を示します
(PでありかつQである)でない !(P && Q) ⇔ PでないまたはQでない !P || !Q
(PであるまたはQである)でない !(P || Q) ⇔ PでないかつQでない !P && !Q
どこかの女の子が自分の彼氏の条件として、「(貧乏または不潔)でない」と言ったとしましょう。 この条件式は、上記の書換え規則により「貧乏でないかつ不潔でない」と言えることができます。 そんな世迷い言はともかく、Javaでどのように記述するか例を見てみましょう。 コメントの中に等しい記述を書いておきます。 2番目の例は数直線を描いて確かめてみて下さい。
!(x==0 || x==100) // !(x==0) && !(x==100) もしくは x !=0 && x != 100 !(100<=x && x<=200) // !(100<=x) || !(x<=200) もしくは x<100 || x>200
それ以外にも、不等号や等号に関して、簡単な書換え規則が考えられます。 いくつか例を紹介しますが、ここに挙げている以外にも自分で考えてみて下さい。 下記の例でAとBは何らかの式であると仮定します。
| !(A == B) | A != B | 等号と不等号の変換 | ||
| !(A != B) | A == B | |||
| A <= B | A < B || A == B | 等号付き不等号の分解 | ||
| A >= B | A > B || A == B | |||
| !(A <= B) | A > B | 逆の不等号への変換(その1) | ||
| !( A >= B ) | A < B | |||
| !(A < B) | A >= B | 逆の不等号への変換(その2) | ||
| !( A > B ) | A <= B |
■if文とif式
★条件が満足されたときだけ実行される条件分岐(if文)
この条件分岐は、次のように記述します。
▼if文:
if ( 条件式 ) ブロック
条件式が満足されなかった場合は、何もせずに次の処理に実行が移ります。
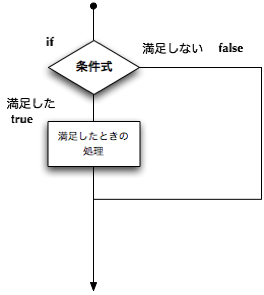
たとえば、以下のプログラムは、マイナスの数が入力されても、絶対値を表示するようになっています。 mainメソッドの中だけを記述しています。
//入力された値の絶対値を表示するプログラム
int ikachan;
ikachan = Terminal.inputInteger( "整数を入力して下さい: " );
if ( ikachan < 0 ) {
ikachan = - ikachan;
}
System.out.println( "入力された整数の絶対値は" + ikachan + "です。" );
★条件が満足されたないときの処理も指定できる条件分岐(if else文)
▼if文:
if ( 条件式 ) ブロック
else ブロック
最初の条件分岐の記述方法では、条件に該当しない場合は、何もしないで次の処理に実行が移りますが、 こちらの条件分岐では、該当しない場合に、2番目に書かれたブロックを実行するようになります。
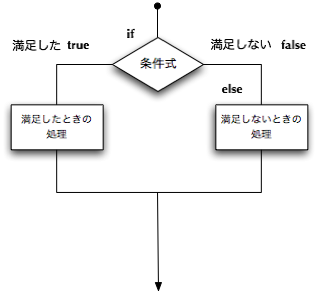
次のプログラムは、入力された数が偶数か、奇数かを表示するものです。 整数剰余を用いているところに注目してください。 またもや、mainメソッドの中だけを記述しています。
//入力された数が偶数か、奇数かを判定するプログラム
int verifier = Terminal.inputInteger( "正の整数を入力して下さい" );
if ( verifier % 2 == 0 ) {
System.out.println( verifier + "は偶数です" );
} else {
System.out.println( verifier + "は奇数です" );
}
よく間違う文法エラーは、「else 」の後に反対の条件式を書いてしまうことです。 律儀な人に多いのですが、既に最初の条件式で満足しないことがわかっているのですから、 反対の条件をわざわざ書く必要はありません。
★複数の条件を指定できる条件分岐(if else if文)
if文については、第3番目の書式で代用できますので、それで記述します。以下の記述で、[ A ]は、Aを省略可能であることを 示し、[ A ]…はAを0回以上繰り返せることを示しています。
▼if文:
if ( 条件式 ) ブロック
[ else if ( 条件式 ) ブロック ]…
[ else ブロック ]
上記の文法の規則の中で[]は、省略可能であることを意味しています。また、…は、何回繰り返しても 良いことを意味しています。ですから、最後の「そうでないならば」のブロックは省略することができますし、 途中の「else if ( 条件式 ) ブロック」の部分は、何回(0回も含む)繰り返しても良いことになります。 途中のブロックが省略された場合は、2番目の条件分岐と同じ意味ですし、途中のブロックと最後のelse に付随するブロックがすべて省略された場合は、1番目の条件分岐と同じです。最後のブロックだけ省略することも可能です。 その場合は、すべての条件に当てはまらないときは何もせずに次の処理へ進みます。 途中のブロックが1回以上ある場合は、条件式は上から順番に調べられていきます。
else if 文が複数ある場合は、上から順番に条件式を評価し、条件を満足するif文の後で指定されたブロックを選択し、 実行するということです。条件式が上から順番に一つずつ評価されることに注意してください。
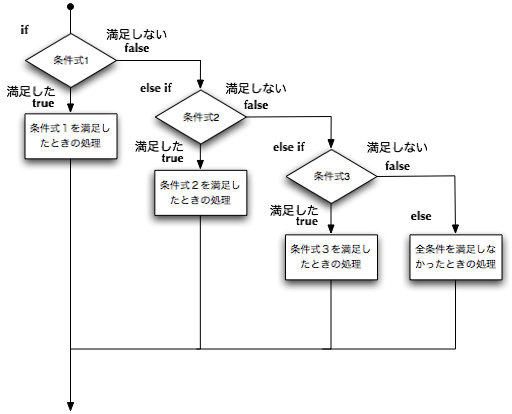
たとえば、整数型の変数xに何らかの正の整数値が入っているものとしますと、以下の記述は、上から順番に条件式を評価して、 対応するメッセージをターミナルに出力します。またもや、mainメソッドの中だけを記述しています。
// 成績判定プログラム
int score = Terminal.inputInteger( "あなたの成績を入力して下さい(100点満点)" );
if ( x >= 80 ) { // 80以上
System.out.println( "成績はA" );
}
else if ( x >= 60 ) { // 60以上でかつ80未満
System.out.println( "成績はB" );
}
else if ( x >= 40 ) { // 40以上でかつ60未満
System.out.println( "成績はC" );
}
else { // 40未満
System.out.println( "落第" );
}
あるいは、現在の時間が整数型の変数hourに求まっているとしましょう。 このときに、8時と12時と、午後7時(19時)ならば、食事に行くような条件分岐を書いてみましょう。 またもや、mainメソッドの中だけを記述しています。
// 規則正しい食生活プログラム
int hour = Terminal.inputInteger( "現在何時でしょうか(0〜23)? " );
String message;
if ( hour == 8 ) { message="朝食を食べましょう"; }
else if ( hour == 12 ) { message="ランチを食べましょう"; }
else if ( hour == 15 ) { message="午後の紅茶を飲みましょう"; }
else if ( hour == 19 ) { message="ディナーを食べましょう"; }
else { message="食べ過ぎにご用心"; }
System.out.printf( "今%dならば、%s\n", hour, message );
■if式
条件文を使いますと、いろいろな場合分けができるのですが、 代入文などではいちいち条件分岐を使うのが面倒な場合があります。 たとえば、次のプログラムの断片を考えてみましょう。
int month =Terminal.inputInteger( "月を入力(1〜12): " );
int season;
if ( month < 9 ) { season = 1; } else { season = 2; }
これをもっと簡単に記述するための式が用意されています。これを一般にif式と呼んでいます。
▼if式:
( <論理式> ) ? <trueのときの式> : <falseのときの式>
このif式を使いますと、さきほどの条件分岐は一つの代入文で記述することができます。
int month = Terminal.inputInteger( "月を入力(1〜12): " ); int season = ( month < 9 ) ? 1 : 2;
このように、if文がなくなり、簡潔に記述できるので、これを愛用するプログラマはかなり多いのですが、 あまり多用しすぎると、かえってプログラムを読みにくくします。 使うときには読みにくくなるかどうか、いつも注意しながら使いましょう。 なお、if式もネストさせることができます。例えば、季節毎に変数の値を1〜4まで変えたいときには、 if式をネストさせて、次のように記述します。これは、if〜else if文に相当します。
int month = Terminal.inputInteger( "月を入力(1〜12): " ); String season = ( month <= 3 ) ? "winter" : ( month <= 6 ) ? "spring" : ( month <= 9 ) ? "summer" : "autumn";
★実習3-5 割り切れる数どうかの判定
ある数をダイアログかターミナルで入力してもらって、それが13で割り切れる数かどうか判定します。 クラス名はPractice0305という名前で新規クラスを作成し、コンパイルし、実行しなさい。
☆課題3-6 元号と西暦の変換
まず、次のような表示を出します。「明治=1,大正=2,昭和=3,平成=4,西暦=5」の中から選んで下さい。 1〜4までの場合は、元号と年から西暦を求めます。5の場合は、逆に西暦から元号と年を求めます。 さて、次に年を入れてもらいます。たとえば、ユーザが4(=平成)を入力し、19を入力してもらったら、 「平成19年」ということですから、「西暦」と表示し、その後「2007」と表示させます。 あるいは、ユーザが5(=西暦)と入力し、1998を入力したら、「平成」と表示し、その後「10」と表示します。 コンソールに一行として出力しても構いません。 ちなみに、明治から平成までの元号の元年(最初の年)は、以下の通りです。 もし、西暦で1868年以前を入力された「明治以前」という表示だけで結構です。 また、西暦1989年以降は、すべて「平成」と年数で表示してください(たとえ、3080年でも)。 クラス名はNengoConverterという名前で新規クラスを作成し、コンパイルし、実行しなさい。
| 明治元年 | 西暦1868年 | 昭和元年 | 西暦1926年 | |
| 大正元年 | 西暦1912年 | 平成元年 | 西暦1989年 |
☆課題3-7 閏年かどうかを判定する
現在採用されているグレゴリオ暦では、 閏年の計算を以下のように求めています。 これで1暦年は平均365.2425日で、約3320年に1日の割合で暦と季節がずれることになります。 1年の平均回帰年(約365.242199日)と 食い違いがあるからです。
- 西暦の年が4で割り切れる年は閏年とする。
- ただし、その中で100で割り切れる年は閏年とはしない。
- ただし、その中で400で割り切れる年は閏年とする。
365+1/4-1/100+1/400=365+0.25-0.01+0.0025=365.2425という計算になります。 ちなみに、古代マヤ文明のカレンダーでは、1暦年を365.2420日としており、グレゴリオ暦よりも精度が高いのでは ないかとも言われています。 課題はターミナルから西暦のある年を入力してもらい、それが閏年かどうか表示するプログラムを作成するという ものです。 クラス名はLeapYearで作成し、コンパイルし、実行します。 実行時に1900年、2000年、2004年、2007年などを入力値として入れてみて、それぞれ平年、閏年、閏年、平年であると 表示されるかどうか確かめなさい。
■switch文
Javaの条件分岐には、if文の他にswitch文という文があります。 switch文は値に応じて複数の選択肢がある場合に便利な文です。switch文の記述方法は次の通りです。
▼switch文
switch ( 式 ) {
case 式: 文 // 何個あっても可
default: 文 // 省略されても可
}
しかし、上記では記述では解りにくいので良く使われる例を示します。
switch ( 式 ) {
case 式1:
式の評価結果が式1の評価結果と同じ時に実行される内容
break;
case 式2:
式の評価結果が式2の評価結果と同じ時に実行される内容
break;
...
default:
式1、式2、...のどの式にも合致しなかった時に実行される内容
break;
}
上記が実際にswitch文を使う際の書式です。switch文の中にはcase節が幾つか存在します。 switch文が実行されると、switch文の括弧の中の式を評価し、その結果が一致するcase節まで飛び、 そこから実行が開始されます。通常は次のcase節の前にbreak文があり、ここでswitch文の実行が中止されます。 break文が無いとそのまま次のcase文の下の部分も実行されることになります。 switch文の括弧の中の式を評価した結果が、どのcase節の式にも合致しない場合はdefault節から実行されます。 上記の記述は以下のようなif else if文と同等となります。
if ( 式 == 式1 ) {
式の評価結果が式1の評価結果と同じ時に実行される内容
} else if( 式 == 式2 ) {
式の評価結果が式2の評価結果と同じ時に実行される内容
} ...
else {
式1、式2、...のどの式にも合致しなかった時に実行される内容
}
たとえば、1から10までの序数を英語で表記するスクリプトの例を以下に示します。
String ordinal = ""; // 序数を示す文字列
for ( int n=1; n <= 10; n = n + 1 ) {
switch ( n ) {
case 1: ordinal = "First"; break;
case 2: ordinal = "Second"; break;
case 3: ordinal = "Third"; break;
default: ordinal = n + "th"; break;
}
System.out.print( ordinal + " " );
}
System.out.println();
■while文
★while文による繰返しの一般的な書式
Javaも含めて、一般のプログラミング言語では、n回繰返しができる制御文が用意されていません。 (ただし、AppleScriptなどの一部のスクリプト言語では、紹介しましたように用意されています。) その替わりに、この旧来より存在する、条件式を用いた繰返し文だけが用意されています。 これは「条件繰返し文(Conditional Loop Statement)」と呼んでいます。
▼while文
while ( 論理式 )ブロック
最初に書かれる条件式は、繰返しが行なわれるたびにチェックされます。 論理式で記述された条件式を満足している限り、ブロック内の 処理が実行されます。もし、条件式を満足しなくなったら、繰返しを終了し、その次の処理へプログラムは 継続します。 すなわち、while文は、上記の論理式が満足されている間は、ブロックを繰り返します。 ですから、まず最初にブロックが実行される前に、論理式が評価されます。 これらの論理式は、「継続条件」と呼ばれていて、繰返しされるときに毎回評価され、 満足される間は繰返しが継続されます。 論理式は、満足される場合は「true」、 満足されない場合は「false」という論理値として評価されますから、 永遠繰返し文のように論理値自体を記述しても構わないのです (ただしfalseを記述するとコンパイラに「この繰返しは実行されないよ」と注意されます)。 論理式がtrueに評価されたならば、ブロックが実行されます。 そしてその後、また論理式が評価されます。その繰返しになります。 論理式がfalseに評価されたときは、繰返しを終わります。 次の処理が記述されいれば、その処理に実行が移ります。
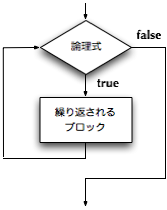
while文のセマンティックス(実行の意味)
☆繰返しと型の表現範囲についての注意
//ループ変数を掛けていく例(2のn乗を出力する)
int m = 1;
int n = 0;
while ( m < 2100000000 ) {
System.out.print( "2の" + n + "乗は" );
System.out.println( m );
m = m * 2;
n = n + 1;
}
上の例は一見正しく動きそうに見えますが、整数の表現範囲が21億4748万3647なので、最後に21億4748万3648 になったところで、ビット落ちしてしまって(この現象を「オーバフロー:Overflow」と呼んでいます)、 -21億4748万3648となり、条件を満足してしまい処理が続きます。オーバフローはその後も起こり、すべてのビットが 追い出されて、数値的には0になってしまい、永遠に処理が続いてしまいます。 このように、計算結果が整数の表現範囲を超えてしまうかどうかについても考えておくことが必要です。
■do〜while文
do〜while文は、while文と似たような動作をしますが、条件を評価する場所が異なります。下記にdo〜while文の書式を示します。
▼do〜while文:
do {
// 1回目と、条件が成立する間、実行を繰り返す処理ブロック
} while (継続条件);
do〜while文は、ブロックの中を1回は必ず実行し、その後に継続条件を判定します。do〜while文はwhile文に比べると、あまり使われる頻度は多くありません。アルゴリズムにおいて、最低でも1回は実行しなければならないという状況が少ないからです。後で、break文の例題でも示しますが、 入力のガードをdo〜while文で記述してみましょう。
do {
int dice = Terminal.inputInteger( "1から6までの数を入力して下さい" );
} while ( dice <1 || dice > 6 );
範囲外のときにエラーであることが表示されず、入力が繰り返されるだけですので、 少し不親切です。そんなこともあって、break文で代用される場合が多いのです。
■for文
while文の場合、繰返しの中でしか使わないループ変数の宣言やその最初の値を代入する場合など、 while文が始まる前に独立して書かなければなりませんでした。 これらの不便を解消してくれる強力な繰返しのための構文が存在します。 それが以下に述べるfor文です。Java言語のfor文は、内部で変数の宣言もできます。 言霊の回数繰返し文もfor文として記述することが多いと思われます。
for ( 最初に行なうこと ; 継続条件 ; 繰り返すときに行なうこと ) {
繰り返したい内容
}
書式では、for文の4つの部分がすべて記述されいますが、どの部分も、省略することが可能です。 ただし、継続条件が省略されたときは、そこにtrueが書いてあるものとみなします。 この場合、永遠に繰返すこととなるでしょう。
for文の意味ですが、それぞれの部分について、もう少し詳しく実行の過程を追ってみましょう。
- 最初に、繰返しを行なう前に「最初に行なうこと」の式が評価されます。 これは、繰返しを1つもしない場合でも実行されます。
- 次に、「継続条件」を満足しているかチェックします。 条件式を評価し、真(true)であれば繰返しを継続しますし、 偽(false)であれば繰返しを止めて次の処理に制御を移します。
- 繰返しを行なうときは、まず「繰り返したい内容」の方を先に実行します。
- そして、次の繰返しに移る前に「繰り返すときに行なうこと」の部分を評価します。
- 以降の繰返しは、2.のところから行なわれます。
以上をfor文の各部分をABCDという形で分け、制御の流れを図示しますと、次のようになります。
for ( A; B; C ) {
D; A→B→D→C→B→D→C→ .... B→D→C→B→次へ
} ↑
B→D→C→が何回か繰り返される
☆for文の初期値設定とループ変数
for文の「最初に行なうこと」の部分には、変数の宣言ができます。 変数の宣言をする場合は、初期値を代入する必要があります。 この変数を使って、10回の繰返しをする記述の仕方をみてみましょう。 ループ変数としてcountという名前で整数の変数を宣言しています。
for ( int count=0 ; count < 10; count=count+1 ) {
System.out.println( "Count up: " + count );
}
上の繰返しは、変数countを0から9まで変化させて、計10回の繰返しを行なわせています。 毎回の繰返しの中で、変数の値を端末画面に出力しています。 「count=count+1」は、「count+=1」と省略形で記述したり、「count++」と記述することも できます。以下の記述では、インクリメント演算子「++」を使った記述も出てきますが、 変数の値を一つ増やすということを憶えておいてください。 なお、for文の中で宣言された変数は、for文の繰返しのブロック内でしか用いることができません。
for ( int x=1 ; x<10 ; x++ ) {
sum = x + 5; // このブロックの中では、変数xを用いることができる
}
int y = x + 10; // エラー、繰返しが終わった後は、変数xを用いることができない
for文のそれぞれの部分に関して、さまざまな記述ができますが、 たとえばループ変数の値を繰返しする中で増やしていく場合は、それぞれの値を設定する目安として、 次のように考えるといいでしょう。これはwhile文のときにも説明しました。
for ( int i = 初期値; i < 上限値 ; i = i + 間隔 ) { ...... }
このようにすると繰返しをする回数は、⎡(上限値 - 初期値)/間隔⎤で求められます。 ループ変数と上限値との比較が不等号で行なわれていることに注意してください。 たとえば、次の繰返しは、7回繰返しをします。
for ( int w = 10; w < 150; w += 20 ) { // w = w + 20と記述しても良い
System.out.println( "The value of w is " + w + "." );
}
☆for文のループ変数のトレース
1から10までの値の総和を求めるプログラムの断片を記述してみましょう。
int sum = 0;
for ( int i = 1; i<= 10 ; i++ ) {
System.out.println( "Trace i: " + i );
sum = sum + i;
System.out.println( "Trace sum: " + sum );
}
System.out.println( "Final value of sum: " + sum );
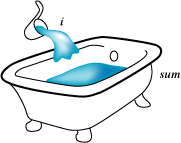
変数の値がどのように移り変わっていくのか注意してください。 for文の中で宣言された変数は、繰返しを制御するためのループ変数になっています。 特に、ループ変数とループ変数に関係のある変数の変遷を追っていく(トレースする)ことは重要です。 上記の総和のプログラムにおいては、変数sumの値とループ変数 i の値の移り変わりに注目してみましょう。
sum: 0 → 1 → 3 → 6 → 10 → 15 → 21 → ....
i: 1 → 2 → 3 → 4 → 5 → 6 → 7 → ....
2つの代入 sum = sum + i; と i++ によって、このように、値が相互に変わっていきます。 sumは、最初が0でどんどん値が足し込まれています。 これは、例えば風呂桶などに、小さな桶を何回も使って水を足していくのに似ています。
☆while文とfor文との互換性
for文をwhile文について、両方を書き直してみましょう。 for文がwhile 文に比べて強力な記述ができることがわかります。
while文をfor文で書き直してみる
|
for文をwhile文で書き直してみる
|
たとえば、例として1から100までを表示するプログラムをwhile文とfor文の両方で記述してみましょう。
// while文での記述
int i=1;
while ( i <= 100 ) {
System.out.print( i + " " );
if ( i % 10 == 0 ) { System.out.println( ); } // 10個ごとに改行
i++; // i = i + 1;と記述しても良い
}
System.out.println( ); // 改行の出力
// for文での記述
for ( int i=1; i <= 100; i++ ) {
System.out.print( i + " " );
if ( i % 10 == 0 ) { System.out.println( ); } // 10個ごとに改行
}
System.out.println( ); // 改行の出力
☆練習問題 3-8 カレンダーの表示
- 1つの月についてカレンダーのように日の数を表示するアプリケーションを記述しなさい。
- その月が何曜日から始まるかを0(日曜日)〜6(土曜日)の間で入力してもらい、 曜日を調整したカレンダーを表示するスクリプトを記述しなさい。Practice0308という名前にします。
■break文
Javaには繰返しのブロックの中に書ける脱出文(break文)というのがあります。 break文は、forやwhile文などの繰返しから強制的に脱出するという効果を持ちます。 break文を使うと、一番内側の繰返し文(ブロック)から脱出することができます。
▼break文:
break;
break文は単体で使われることはなく、if文と脱出条件を指定して、途中脱出するのに用いられます。 特に、繰返しの中でAとBという処理があって、 最後の繰返しではBの部分をしたくないような場合に使われます。 以下に、その典型的な使用例の記述の仕方を示します。
while ( true ) {
Aの部分
if ( 脱出条件 ) { 終わるときの処理; break; }
Bの部分
}
たとえば、よく表示で使うことが多いのですが、1,2,3,4, ....というように、表示される数列の途中だけ、 カンマを表示したい場合があります。次の繰返しはwhile文を使ってみましたが、if文で10を越えたときの ループ変数iを表示して、カンマを表示せずに改行させて繰返しを脱出しています。printLine( );は改行だけを 表示しています。条件繰返し文で記述するされるのは、継続条件でしたが、break文を用いたif文のところで 使われるのは「終了条件」であることに注意して下さい。丁度、反対の条件を記述します。 いつものようにmainメソッドの中だけを記述します。
int i = 1 ;
while ( true ) {
System.out.print( i );
if ( i >= 10 ) { System.out.println( ); break; }
System.out.print( ", " );
i ++ ;
}
このプログラムによって、次のような出力を得ます。最後にカンマがついていないことに注意してください。
1, 2, 3, 4, 5, 6, 7, 8, 9, 10
☆実習3-9 素数を求めるプログラム
次のプログラムは、mainメソッドの中のみを記述しています。 プログラムの内容は、50ぐらいまでの数について表示される素数の間に「,」を表示しますが、 最後は表示されないようにしています。繰返しが終わった後にprintLineを呼んでいますが、これは改行だけを 出力するために行なっています。 素数(prime)を求めるのは、試す数(verifier)で割り切れるかどうかを求めています。 もし、2からその数までで割り切れてしまった場合は素数ではありませんので、 内側の繰返しを終わった段階で(verifier < prime)という状態になります。 割り切れない場合は内側の繰返しを回り切って終了しますので(verifier == prime )という状態になります。 クラス名はPrimeTesterという名前でコンパイルして実行して見てください。
for ( int prime = 1; true; prime++ ) {
int verifier = 2;
while ( verifier < prime ) {
if ( prime % verifier == 0 ) { break; }
verifier++;
}
if ( verifier == prime ) { System.out.print( prime ); }
if ( prime > 50 && verifier == prime ) { break; }
if ( verifier == prime ) { System.out.print( ", " ); }
}
System.out.println( );
☆想定外の入力のガード
ユーザから入力を貰うときに、想定外の値を入力される場合があります。 想定外の値が来ると、その後のプログラムの実行内容に支障をきたすような場合は、 繰返しにしておいて、一定の範囲の値だけが入力された場合だけ、繰返しを脱出するようにしておきます。 このように想定外の入力を貰わないようにすることを「入力をガード(Guard)」すると言います。
入力をガードする次のプログラムの断片は、 入力値が1から6の範囲になければ、繰り返すして入力を受け付けないようにしています。
int dice;
String error ="";
while ( true ) {
dice = Terminal.inputInteger( error + "1から6までの数を入力して下さい: " );
if ( dice >=1 && dice <= 6 ) { break; }
error = "数を入力していないか、範囲外です。";
}
■continue文
ループを使っていると、繰返しの途中でそのループを止めたくなったり、 繰返しブロックの中の残りの部分を実行せずに次の周回に移りたくなったりすることがあります。 このような時に使えるのがcontinue文です。break文は繰返し処理をそこで止めて、 繰返しループを抜けてしまいますが、continue文は、処理を途中で止めるというところは 同じなのですが、 繰返し処理自体を止めることはせずに、次の回に移るという部分が異なります。
▼continue文:
continue;
次のプログラムは、continue文を使って、約数の個数と総和を求めています。 繰返しを次の回にスキップさせるという役割で用いられています。
int sum = 0; // 総和を求めるため
int count = 0; // 個数を求めるため
int number = Terminal.inputInteger( "正の整数を入力:" );
for ( int n=1; n <= number; n = n + 1 ) {
if ( number % n != 0 ) { continue; }
sum = sum + n;
count = count + 1;
System.out.println( n + " " );
}
System.out.println( "約数の個数は" + count + "個でその総和は" + sum + "です。" );
■ラベル付きのbreak・continue文
breakやcontinue文は、一番内側の繰返しに対して効果を持ちます。 それに対して、もっと外側の繰返しまで 脱出・継続したい場合は、そのレベルに対してラベルを定義します。 ラベルの定義の仕方は、以下のように、 ラベル名を振り、コロンを付けます。switch文のcase句のラベルと似ていますが、値ではなく、 直接名前を(英字で始まる名前を半角で)記述します。
▼ラベル:
ラベル名:
そのラベルのレベルまで効果を持たせる場合は、以下のようにbreakやcontinueの後に 空白を開けてから、ラベルを指定します。
▼ラベル付きbreak・continue文:
break ラベル名;
continue ラベル名;
下記の例は、iとjの積が特定の値になったら、外側の繰返しまで終わらせるものです。 ラベルのレベルまで脱出するので、脱出する先が、ラベルのあるプログラム上の位置では ないことに注意して下さい。
escapeLevel: // ラベルの指定
for ( int i=1; i <=10; i ++ ) {
for ( int j=1; j <= 10; j++ ) {
if ( i * j == 63 ) {
System.out.printf( "i: %d j: %d\n", i, j );
break escapeLevel;
}
}
}
// 脱出先はここになります
System.out.println( "terminated." );
下記の例は、iとjの積が特定の値になったら、外側の繰返しを次に進めます。
nextLevel: // ラベルの指定
for ( int i=1; i <=10; i ++ ) {
for ( int j=1; j <= 10; j++ ) {
if ( i * j == 63 ) {
System.out.printf( "i: %d j: %d\n", i, j );
continue nextLevel;
}
}
}
■return文
return文は、値を戻すときに使われますが、値の指定がない場合は、単にそのメソッドを終了させるときに 用います。
▼return文:
return;
下記の記述がmainメソッドにあった場合、マイナスの値を入力したら、 プログラムが終了します。
int sum = 0;
while ( true ) {
int value = Terminal.inputInteger( "正の整数値を入力: " );
if ( value < 0 ) {
System.out.println( "入力値が負なので終了しました。" );
return;
}
sum += value;
System.out.printf( "%d加算後の合計: %d\n", value, sum );
}
■いくつかの典型的な整数の問題
☆素数の別の求め方
実習3-9の素数の求め方以外に、約数の数で素数かどうかを判定することができます。 素数の場合は、1とその数でしか割り切れませんから、約数の個数は2個になります。 2〜1000までの素数を求めてみましょう。
for ( int n=2; n <= 1000 ; n++ ) {
int count = 0; // 約数の個数を保持するカウンタ
// nを割り切れる数がいくつあるか求める
for ( int m = 1; m <= n; m++ ) {
if ( n % m == 0 ) { count++; }
}
// 素数かどうか判定
if ( count == 2 ) {
System.out.print( n + " " );
}
}
System.out.println( );
☆ユークリッドの互除法
2つの自然数の最大公約数を求める方法がユークリッドの互除法です。 2つの数をa, b(ただしa > b)とし、aとbの剰余をr (r = a % b)とすると、 a と b との最大公約数は b と r との最大公約数に等しいという性質が成り立つというものです。 この性質を利用して、 b を r で割った剰余、 除数 r をその剰余で割った剰余、 と剰余を求める計算を逐次繰り返すと、剰余が 0 になった時の除数が a と b との最大公約数と いう方法です。
int n = Terminal.inputInteger( "正の整数を入力して下さい。" );
int m = Terminal.inputInteger( "別の正の整数を入力して下さい。" );
// nの方が大きくなるように入れ替える
if ( n < m ) { int temp = n; n = m; m = temp; }
while ( n % m != 0 ) {
int save = m;
m = n % m;
n = save;
}
System.out.printf( "最大公約数は%dです。\n", m );
nとmの最大公約数をgcdとすると、nとmの最小公倍数lcmは、lcm=n * m / gcdとなることを 利用して、最小公倍数も合わせて求めて下さい。
☆素因数分解
素因数分解とは、 ある正の整数を素数の積の形で表すことです。 ただし、1 に対する素因数分解は 1 と定義します。 たとえば、360 を素因数分解すると、以下のように、2と3と5という素数の積で表されます。
360 = 23 × 32 × 51
素因数分解には、いろいろなアルゴリズムがあるのですが、簡単に素数で割っていくものを 記述してみます。
int target= Terminal.inputInteger( "2以上の整数を入力:" );
for ( int n=2; n <= target; n++ ) {
// 素数を求める
int count = 0; // 約数の個数を保持するカウンタ
// nを割り切れる数がいくつあるか求める
for ( int m = 1; m <= n; m++ ) {
if ( n % m == 0 ) { count++; }
}
// 素数ならば割ってみる
if ( count == 2 ) {
while ( target > 1 ) {
// 割り切れないのであれば素因数ではない
if ( target % n != 0 ) { break; }
System.out.printf( n + " " );
// nで割り切れるので、targetをnで割り、小さくしておく
target = target / n;
}
// 最終的にtargetが1になれば、終了する
if ( target == 1 ) {
System.out.println( );
break;
}
}
}
☆階差式
階差機関に書かれているように、 n次の多項式の結果を記した数列は、n次の階差まで求めると一定の定数になります。 そのため、次数の高い多項式も、すべて足し算で計算できます。 たとえば、xの2乗について考えてみましょう。 0から順に初めて、計算結果を求めていき、その階差を取ると次のようになります。
x: 0 1 2 3 4 5 6 7 8 9
x2: 0 1 4 9 16 25 36 49 64 81
\/ \/ \/ \/ \/ \/ \/ \/ \/
第1階差: 1 3 5 7 9 11 13 15 17
\/ \/ \/ \/ \/ \/ \/ \/
第2階差: 2 2 2 2 2 2 2 2
これを利用し、任意のpx2 + qx + rという二次方程式について、掛け算を使わないで、計算するプログラムを作ります。 px2 + qx + rの第1階差は、p*(2 *x+1)+q(すなわちp*(x+x+1)+q)になります。 第2階差は、2p(すなわちp+p)になります。x=0のときの、 最初の計算結果(初期値はr)、第1階差(初期値はp+q)、第2階差(p+pで一定)を求めておき、 それを求められる数にxが達するまで足し合わせていきます。
int p = Terminal.inputInteger( "xの2乗の係数を整数で入力:" );
int q = Terminal.inputInteger( "xの1乗の係数を整数で入力:" );
int r = Terminal.inputInteger( "xの0乗の係数を整数で入力:" );
int result = r;
int diff1 = p + q;
int diff2 = p + p;
for ( int x = 0; x <= 100; x++ ) {
System.out.printf( "xが%dのときの計算結果: %d\n", x, result );
result = result + diff1;
diff1 = diff1 + diff2;
}
なお、一般のn次多項式の場合の各階差の初期値は、上記リンクのWikipediaの中に初期値が 書かれています。
☆ピタゴラス数
a2+b2=c2を満たすような正の整数、 a, b, cの組み合わせのことをピタゴラス数と呼びます。 また、aとbとcが互いに素(最大公約数が1)の組み合わせの場合、原子ピタゴラス数と呼びます。 2〜100の間で、ピタゴラス数を表示してみましょう。
for ( int a = 2; a <= 100; a++ ) {
for ( int b = a; b <= 100; b++ ) {
for ( int c = b; c <= 100; c++ ) {
if ( a * a + b * b == c * c ) {
System.out.printf( "( %d, %d, %d )\n", a, b, c );
}
}
}
}
上記のプログラムでは、繰返しの回数を少なくするために、a <= b <= cという前提条件で 繰返しを行なっています。
☆練習問題 3-10
- 2〜10000までの完全数を求めてみましょう。 完全数は、その数を除く約数の総和が、その数自身と等しいものです。 クラス名はCompleteNumbersで
- メルセンヌ数(Mersenne number)とは、 2のべき乗よりも 1 小さい自然数、すなわち 2n − 1 の形の自然数のことを指します。 また、素数であるメルセンヌ数をメルセンヌ素数と呼びます。 2〜10000までのメルセンヌ素数を求めてみましょう。 クラス名は、MersenneNumbersで
- 2〜1000の範囲で原子ピタゴラス数の組み合わせを求めてみましょう。 クラス名は、PrimitivePythagoreansにて
- 3次多項式の計算結果を階差式で求めてみましょう。xの3乗から0乗までの項の4つの係数を まず入力してもらいます。 クラス名は、ThreeDegreePolynomialsにて
- 1〜100までの序数を表す英語を求めてみましょう。 下一桁が1のときは"first"、2のときは"second"、3のときは"third"になります。 それ以外は"th"を付ければOKです。 ただし、11番目は"eleventh"、12番目は"twelveth"となります。 それ以外は、たとえば、41番目は、"forty first"で、54番目は"fifty fourth"になります。 クラス名は、OrdinalNumbersで
3−3.アプレットでのグラフィックス
■Graphicsクラスの描画メソッド抜粋
| 標記 | 説明 |
|---|---|
| drawLine( x1, y1, x2, y2 ) | 座標(x1, y1)から座標(x2, y2)まで線を引く、パラメータはすべてint型 |
| drawRect( x, y, w, h ) fillRect( x, y, w, h ) |
座標(x, y)を左上の頂点に持つ四角形を幅w、高さhで描く/塗り潰す。パラメータはすべてint型、wとhは非負 |
| drawOval( x, y, w, h ) fillOval( x, y, w, h ) |
座標(x, y)を左上の頂点に持ち、幅w、高さhの四角形の内接楕円を描く/塗り潰す。 パラメータはすべてint型、wとhは非負 |
| draw3DRect( x, y, w, h, push ) fill3DRect( x, y, w, h, push ) |
座標(x, y)を左上の頂点に持ち、幅w、高さhの四角形のを描く/塗り潰す。 pushがtrueだと前に凸に見えるようにする。falseだと凹に見えるようにする。 パラメータはx, y, w, hがint型、wとhは非負、pushはboolean型 |
| drawArc( x, y, w, h, st, diff ) fillArc( x, y, w, st, diff ) |
座標(x, y)を左上の頂点に持ち、幅w、高さhの四角形の内接楕円の弧を描く/中心から弧までを塗り潰す。 stは開始角度、diffは角度差、360度体系で指定する。開始角度は、東の方向からで、反時計回りに角度差を指定する。 パラメータはすべてint型、wとhは非負 |
| drawRoundRect( x, y, w, h, rw, rh ) fillRoundRect( x, y, w, h, rw, rh ) |
座標(x, y)を左上の頂点に持ち、幅w、高さhの四角形を描く/塗り潰す。 四角形は、四隅が丸く切り取られており、この丸みの幅がrw、高さがrhで指定される。 パラメータはすべてint型、wとhは非負 |
| drawString( s, x, y ) | 座標(x, y)を左下の頂点に持つ文字列sを描画する。x, yはint型、sはStringクラス |
| clearRect( x, y, w, h ) | 座標(x, y)を左上の頂点に持ち、幅w、高さhの四角形領域をバックグラウンドカラーで塗り潰し、クリアする。パラメータはすべてint型、wとhは非負 |
以下のように描画の際の属性を設定することができます。
| 標記 | 説明 |
|---|---|
| setColor( c ) | これ以降の描画色をColorクラスのcに基づいて行なう。 |
| setFont( f ) | これ以降のdrawStringでのフォントをFontクラスのfに基づいて行なう。 |
標準では、Colorクラスに以下の値が設定されており、それぞれ色を示しています。
Color.red Color.green Color. blue Color.yellow Color.cyan Color.magenta
Color.orange Color.pink Color.black Color.white Color.gray Color.lightGray Color.darkGray
一般的なRGB値に基づくColorとFontの設定については、次の講義で説明します。
■繰返しと描画
☆drawLineを使って
drawLineの2番目と4番目のパラメータは、それぞれy座標を示していますので、同じ値にすると水平線が描けます。 同じように、drawLineの1番目と3番目のパラメータは、それぞれx座標を示していますので、同じ値にすると垂直線が描けます。 以下は、これを利用して繰返しで描画したものです。アプレットのpaintメソッドの中だけを示しています。
 |
 |
for ( int n=4; n <= 400; n+= 4 ) {
g.drawLine( 4, n, 400, n );
}
|
for ( int n=4; n <= 400; n+= 4 ) {
g.drawLine( n, 4, n, 400 );
}
|
斜め線は垂直線で、3番目のパラメータに勾配の文だけプラスすれば描画できます。 また、パラメータの位置を変えたものを描画してみます。
 |
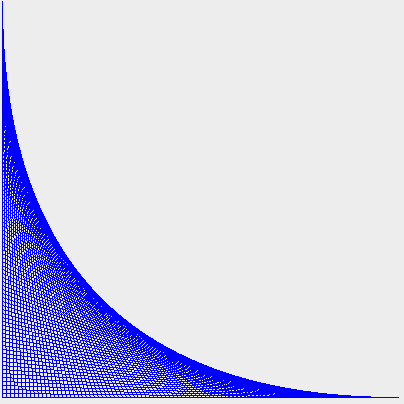 |
for ( int n=4; n <= 400; n+= 4 ) {
g.drawLine( n, 4, n+200, 400 );
}
|
for ( int n=4; n <= 400; n+= 4 ) {
g.drawLine( n, 4, 400, n );
}
|
☆drawRect/drawOvalを使って
drawRectやdrawOvalでは、3番目と4番目のパラメータが幅と高さを示します。 大きさを変えないで、開始座標だけ変えていけば、同じ形のままずれていきます。 また、幅と高さをずらす量分だけ小さくすると、右下に揃ってしまいます。
 |
 |
for ( int n=4; n <= 200; n+= 4 ) {
g.drawOval( n, n, 400, 400 );
}
|
for ( int n=4; n <= 400; n+= 4 ) {
g.drawOval( n, n, 400, 400-n );
}
|
入れ子の形にするには、四角をずらした2倍の長さだけ引かないと中心で揃いません。 drawRectを使って多重の繰返しを使えば、格子のような図を描くことも可能です。 アプレットのpaintメソッドの中だけを示しています。
 |
 |
for ( int n=4; n <= 200; n += 4 ) {
g.drawRect( n, n, 400-n*2, 400-n*2 );
}
|
for ( int i=1; i <= 10; i++ ) {
for ( int j=1; j <= 10; j ++ ) {
if ( ( i + j ) % 2 == 0 ) {
g.drawRect( i *40, j * 40, 35, 35 );
} else {
g.fillRect( i *40, j * 40, 35, 35 );
}
}
}
|
drawOvalを使って、高さだけを変えるようにしてみました。それに合わせてx座標も変えてみたのは、右側になります。
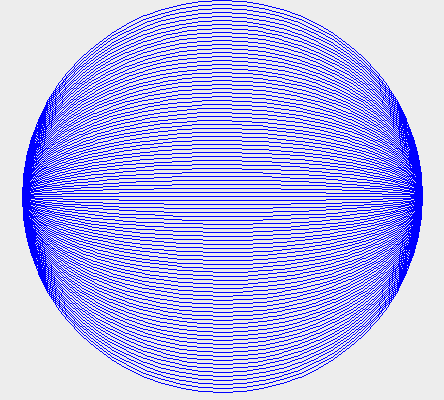 |
 |
for ( int n=4; n <= 200; n+= 4 ) {
g.drawOval( 40, n, 400, 400-n*2 );
}
|
for ( int n=4; n <= 200; n+= 4 ) {
g.drawOval( n, n, 400, 400-n*2 );
}
|
☆drawRountRect/drawArcを使って
drawRoundRectを使って、丸みを変えるようにしてみました。 drawArcでは、開始角度と角度差を変えてみました。
 |
 |
for ( int n=4; n <= 200; n+= 4 ) {
g.drawRoundRect( n, n, 400-n*2, 400-n*2, n, n );
if ( 400-n*2 < n ) { break; }
}
|
for ( int n=4; n < 180; n+= 4 ) {
g.drawArc( n, n, 400-n*2, 400-n*2, n, 360-n*2 );
}
|
☆練習問題 3-13 カレンダーの表示
- 1つの月についてカレンダーのように日の数を表示するアプレットを記述しなさい。
- その月が何曜日から始まるかを0(日曜日)〜6(土曜日)の間で入力してもらい、 曜日を調整したカレンダーを表示するスクリプトを記述しなさい。Practice0313という名前にします。
3−4.整数式でのビット演算
■ビットの論理演算
整数は、内部では2進数で表されていますので、直接2進数の各ビットを制御する演算子があります。 これらの演算子はC/C++からの継承になります。 次のようなビット演算が可能になります。
| 名称 | 演算子 | 意味 | 記述例 |
|---|---|---|---|
| 反転 | ~ | ビットごとに反転させます(complement) | ~value |
| ビット論理積 | & | ビットごとに論理積を取ります(and) | a & b |
| ビット論理和 | | | ビットごとに論理和を取ります(or) | a | b |
| ビット排他的論理和 | ^ | ビットごとに排他的論理和を取ります(exclusive or) | a ^ b |
ビット演算子では、1=true, 0=falseという形で考えてみて下さい。 ビット論理積と論理和では、論理値の演算子に対して、1つ記号が少なくなっています。 また、^という演算子は、べき乗を表すのではなく、ビット排他的論理和として使われていますので注意して下さい。
byte x = 14; // 2進数で00001110 System.out.println( ~x ); // 00001110 → 11110001 (10進数では-15) System.out.println( x & 7 ); // 00001110 & 00000111 → 00000110 (10進数では6) System.out.println( x | 5 ); // 00001110 | 00000101 → 00001111 (10進数では15) System.out.println( x ^ 0xb ); // 00001110 ^ 00001011 → 00000101 (10進数では5)
2の補数にする場合は、反転させて、+1します。そうすると符号が反転します。 以下はbyte型(8bit)の変数を使って、31の2の補数表現を計算しています。 内部的には、すべてint型(32bit)で計算していますので、代入するときは、キャストを 使ってbyte型に戻しています。
byte x = 31; // 2進数で00011111 x = (byte)(~x); // 各ビットを反転 2進数で11100000 x = (byte)(x + 1); // 2進数で11100001 → byteで標記すると-31 System.out.println( Integer.toString( x & 0xff ) ); // 下位8bitだけを表示させる
二項ビット演算子で自己参照によって変数の値を変える場合は、次のように代入演算子の省略形があります。
▼二項ビット演算子による代入演算子:
&= ビット論理積と代入の組み合わせ x &= 3 x = x & 3
|= ビット論理和と代入の組み合わせ x |= 10 x = x | 10
^= ビット排他的論理和と代入の組み合わせ x ^= 3 x = x ^ 3
& (bit and)演算を使えば、以下の例のように、値に対して、特定のビットだけを考慮させることができます。 これを通常「マスク(mask)する」と呼びます。 また、| (bit or)演算を使えば、特定のビットを1にすることができます。 これを「ビットを立てる」と呼ぶことがあります。
int x = 49; // 2進数で110001 System.out.println( Integer.toBinaryString( x & 0xffff ) ); // xの下位16bitだけを表示 System.out.println( Integer.toBinaryString( x ^ x ) ); // 同じ値を排他的論理和を取るとクリアされる System.out.println( Integer.toBinaryString( -x & 0xff ) ); // 下位8bitだけを表示させる System.out.println( Integer.toBinaryString( x | 2 ) ); // 2桁目のbitを必ず1にする
■整数式によるシフト演算
| 名称 | 演算子 | 意味 | 記述例 |
|---|---|---|---|
| 算術右シフト(符号付き) | >> | 各ビットを右にn回シフトし、最上位ビットの値は保存されます。 これによって、符号を温存することができます。 | a >> 3 |
| 論理右シフト(符号無し) | >>> | 各ビットを右にn回シフトし、最上位ビットには各シフトごとに0がはいります。 | b >>> n |
| 左シフト | << | 各ビットを左にn回シフトし、最下位ビットには各シフトごとに0がはいります | a << 4 |
通常の算術右シフト算、左シフト算は、右シフト1回で値を半分にし(整数除算の1/2)、 左シフト1回で値を2倍にすると考えておけば良いでしょう。
System.out.println( 33 >> 1 ); // 整数除算で2で割ったのと同じ、16が表示される System.out.println( 15 << 1 ); // 2倍したのと同じ、30が表示される System.out.println( 5 << 4 ); // 24 = 16倍したのと同じ、80が表示される System.out.println( 429 >> 3 ); // 23 = 8で割ったのと同じ、53が表示される
■演算子の整理
☆2文字以上連続の演算子の一覧表
ここまでで、 2文字以上連続(間に空白を入れてはいけない)演算子(およびコメントなどの記号も含む)がほぼ出揃いました。 以下にその一覧表を示します。 これらの演算子では、記号の間に演算子を入れてしまうと、コンパイラエラーになってしまいます。 また、\uや0xでは直後に16進数を書かないといけません。
|
☆優先順位一覧
これまで出てきた演算子の優先順位の一覧です。上から順番に優先度が高くなっています。 同じ優先順位の演算子は、左結合性を持ちます。ただし、代入演算子だけは、右結合性を持ちます。
|
☆練習問題3-14</h4>
演算結果をわかりやすくするために、 Integer.toBinaryString( )を使って、2進数をすべて8桁で表示するようにしてみなさい。
☆課題問題3-4
Integer.toBinaryString( )は、1となっている最上位ビットまでしか表示しません。 これを指定された桁数上位bitの0も含めて表示するアプリケーションを作成しなさい。
| <<Previous Lecture | Next Lecture>> |