Reversible/Quantum Arithmetic

1 Understanding the Animations and Circuit Diagrams

The circuit diagrams in the table below, in GIF and XFIG formats, are in relatively standard format for quantum computing. Look first at the circuit GIF. Each horizontal line is a single qubit, and time flows left to right. Each vertical line segment is a gate. The small, dark dots indicate control lines, and the large, open circle is the target qubit.

If you look at the VBE adder, you can see that in the first time slot, a bunch of gates are executed concurrently on different qubits, then in later time slots only one or two are.

Compare this to the animation. At the beginning of the VBE example, there is a lot of activity, then it dies down and you can see the carry ripple back and forth across the quantum register. Each sphere is a (logical) qubit. The motion of the arrows indicates only that a gate is being performed, nothing about the actual state. The golden arches are two-qubit and three-qubit gates. Qubits are green when they have been initialized, but no gates have affected them yet. Recently used qubits are red; as they "age", they fade toward blue. This provides visual information about which parts of the qubit register are idle, and which are active.

Now look at the Aqua source, and you'll see the gates, the CCNOTs (control-control-NOT) and the CNOTs (control-NOT). In my Aqua notation, the label at the beginning of a line of source is the time slot in which the gate is executed, and the time doesn't increment until you see the next such label.

2 Architectures

The architectures shown here, AC, TC, and NTC, are described on our taxonomy page and in our paper, quant-ph/0408006.

3 Adders

In order to design a useful computer, one must understand the behavior of its most common uses. Arithmetic naturally forms a core element in any library of functions.

Addition of two n-bit numbers on a neighbor-only architecture is limited to O(n) when non-neighbor architectures can reach O(logn), demonstrating that physical characteristics of a computing device have an important impact on both real-world running time and asymptotic behavior.

The conditional-sum and carry-select adders are our original designs. The other adders come from various papers listed on our recommendations page. VBE is Vedral-Barenco-Ekert, and BCDP is Beckman-Chari-Devabhaktuni-Preskill. The carry-lookahead adder, one of the most promising circuits, is by Draper, Kutin, Rains, and Svore.

adder algorithm	problem	storage	AC	TC	NTC
	size	space

VBE carry ripple	8	24
animation				coming soon	coming soon
GIF				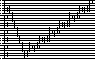coming soon	coming soon
XFIG			vbeadder8.fig	coming soon	coming soon
Aqua source			vbeadder8.ac	coming soon	coming soon

BCDP carry ripple
animation			coming soon	coming soon	coming soon
GIF			coming soon	coming soon	coming soon
XFIG			coming soon	coming soon	coming soon
Aqua source			coming soon	coming soon	coming soon

carry select	6	32
animation				coming soon
GIF				coming soon
XFIG			csel6src.fig	coming soon	csel6bin.fig
Aqua source			csel6src.ac	coming soon	coming soon

conditional sum
animation			coming soon	coming soon	coming soon
GIF			coming soon	coming soon	coming soon
XFIG			coming soon	coming soon	coming soon
Aqua source			coming soon	coming soon	coming soon

carry lookahead	10	35
animation				coming soon	coming soon
GIF				coming soon	coming soon
XFIG			lookahead10src.fig	coming soon	coming soon
Aqua source			lookahead10src.ac	coming soon	coming soon

Table 1: Adder circuit various architectures and choices of algorithm. AC, abstract concurrent architecture. TC, two-qubit gate, concurrent architecture. NTC neighbor-only, two-qubit gate, concurrent architecture.

4 Fast Quantum Modular Exponentiation

See our full paper, "Fast Quantum Modular Exponentiation", for numeric results and the detailed circuits. The paper is available on our publications page.

Abstract:
We have performed a detailed analysis of the impact on modular exponentiation of architectural features and possible concurrent gate execution. Various arithmetic algorithms are evaluated for execution time, potential concurrency, and space tradeoffs. We find that, to exponentiate an n-bit number, for storage space 100n (twenty times the minimum 5n), we can execute modular exponentiation one hundred to seven hundred times faster than optimized versions of the basic algorithms, depending on architecture, for n=128. Addition on a neighbor-only architecture is limited to O(n) when non-neighbor architectures can reach O(logn), demonstrating that physical characteristics of a computing device have an important impact on both real-world running time and asymptotic behavior. Our results will help guide experimental implementations of quantum algorithms and devices.

5 Additional References

See also the Qwiki page on quantum arithmetic for a list of papers on the topic.

Aqua Home

People

Home

Classes

rdv@sfc.keio.ac.jp Copyright 2007 Rod Van Meter
Last modified: $Date: 2007/04/05 02:25:41 $

File translated from T_EX by T_TH, version 3.63.
On 5 Apr 2007, 12:28.