Home >> Columns >> Programming with Real Number
Mathクラスには、数学上使う便利な関数がメソッドとして用意されています。「もう数学なんて嫌!」っていう人が多いかも知れません。 しかし、いざというとき(ないと思っていると案外とあるでしょう)には必要となってきます。 特に、コンピュータグラフィックスや統計処理などのときには、必ず使われます。
メソッド 評価結果の型 意味 E double 自然対数の底を表す PI double 円周率を表す ceil( 実数 ) double 等しいか、大きいうちで一番小さな整数に丸める floor( 実数 ) double 等しいか、小さいうちで一番大きな整数に丸める rint( 実数 ) double 一番近い整数に丸める round( 実数 ) int, long 実数を整数に四捨五入して丸める acos( 実数 ) double cos-1を求める(-π/2〜π/2の間の角度) asin( 実数 ) double sin-1を求める(-π/2〜π/2の間の角度) atan( 実数 ) double tan-1を求める(-π/2〜π/2の間の角度) atan2( 実数 , 実数 ) double 2つの実数をy、x座標とする極角度を求める cos( 角度 ) double cosを求める sin( 角度 ) double sinを求める tan( 角度 ) double tanを求める abs( 数 ) double, float, long, int 絶対値を返してくる exp( 実数 ) double 自然対数のべき乗を求める log( 実数 ) double 自然対数を求める log10( 実数 ) double 常用対数を求める pow( 実数, 実数 ) double べき乗を求める random( ) double 0.0以上1.0未満の間で乱数を返してくる sqrt( 実数 ) double 平方根を求める cbrt( 実数 ) double 立方根を求める IEEEreminder( 実数, 実数 ) double 実数の剰余を正確に求める
計算間違いをすると、ターミナルに数を表示したときに「NaN」と表示されることがあります。 それは、数ではない(非数:Not a Numberの意味です)。 計算にどこか間違いがあって計算できないときに示されます。 それ以外に、実数用のラッパークラスDoubleで定義されている特殊な実数の値を以下に示します。
Double.MAX_VALUE 正の最大有限値
Double.MIN_VALUE 正の最大有限値
Double.NaN 非数
Double.NEGATIVE_INFINITY 負の無限大(−∞)
Double.POSITIVE_INFINITY 正の無限大(+∞)
実数を整数に変換するには、ceil(数学記号で書くと⎡ d ⎤:dは実数値としますあるいは、 floor(数学記号で書くと⎣ d ⎦)および、四捨五入をするround、それから数直線上で一番近い整数にするrintがあります。 それから(int)でのは、Excelなど通常ではtrunc(正式にはtruncate)関数として定義されています。 trunc関数は、数直線上で0に近づくように小数部をなくすものです。
double ceil = Math.ceil( 44.23 ); // ceil = 45.0 double floor = Math.floor( -44.23 ); // floor = -45.0 double closest = Math.rint( -44.23 ); // closest = - 44.0 int round = Math.round( -44.23 ); // round = - 44 int trunc = (int)( -44.23 ); // trunc = -44
整数への変換で注意しなければならないのは、ceilやfloorなどは、正の数の場合と反対になり、それぞれ負の数の場合は、 絶対値的には異なる(ceilは絶対値が小さくなりますし、floorは逆に絶対値が大きくなります)ような数に変換されるということです。 また、roundだけは整数に変換されますが、 他のものは「関数の計算結果が実数のまま」であるということにも注意してください。 また、roundは四捨五入ですので、負の数の場合には下の例のような形になります。コメントとして書かれているのが、計算結果です。
Math.ceil( 23.45 ) // 24.0 Math.ceil( - 23.45 ) // - 23.0 Math.floor( 23.45 ) // 23.0 Math.floor( - 23.45 ) // - 24.0 Math.round( 23.45 ) // 23 Math.round( - 23.45 ) // - 23 Math.round( 23.50 ) // 24 Math.round( -23.50 ) // -23 Math.round( 23.55 ) // 24 Math.round( -23.55 ) // -24 (int) 23.45 // 23 (int) - 23.45 // - 23
ceilとfloorの関係、あるいはroundとfloorの関係を示すのに次のような公式が用いられることがあります。 これで、各関数の関係を判断してください。
Math.ceil( x ) = - Math.floor( - x )
Math.round( x ) = (int) Math.floor( x + 0.5 )
小数第n桁で四捨五入するには、まず、10のn乗(=10n)を、該当の数に掛けてやります。 そこで、roundを使って、整数部を四捨五入します。そして、その後、掛けた分の10のn乗で割ってあげます。 これで、だいたいの場合はうまくいきます。以下のプログラムの断片は、小数第4桁で四捨五入しています。
double value = 23.7383890216; value = value * Math.pow( 10.0, 4 ); value = Math.round( value ); value = value / Math.pow( 10.0, 4 ); printLine( value );
逆に、整数部第n桁で四捨五入するには、これと逆のことを行ないます。つまり、10のn乗で割って、その後、 roundを使って四捨五入して、最後に割った分の10のn乗を掛けてあげます。以下のプログラムの断片は、整数第2桁で四捨五入して います。
int value = 23790216; double temporary = (double)value / Math.pow( 10.0, 2 ); temporary = Math.round( temporary ); value = (int)(temporary * Math.pow( 10.0, 2 ) ); printLine( value );
これをメソッドとして定義してみました。fractionRoundは、対象となる値と小数第何桁で四捨五入するかを引数として貰い、 その結果を返します。また、integerRoundは対象となる値と、整数第何桁で四捨五入するかを引数として貰い、結果を整数で返します。 startメソッドで値を入力してもらい、それぞれのメソッドを呼び出すようにしました。
public void start( ) {
double tester = displayInputDialog( "Input Real Number:", 2.34453 );
tester = fractionRound( tester, 3 );
displayDialog( "Result:" + tester );
int another = displayInputDialog( "Input Integer Number:", 234653 );
another = integerRound( another, 3 );
displayDialog( "Result:" + another );
}
double fractionRound( double value, int place ) {
value = value * Math.pow( 10.0, place );
value = Math.round( value );
return value / Math.pow( 10.0, place );
}
int integerRound( double value, int place ) {
value = value / Math.pow( 10.0, place );
value = Math.round( value );
return (int)(value * Math.pow( 10.0, place ));
}
三角関数、逆三角関数の場合は、角度を指定するときはすべてradian体系(πを基準とする体系)で行なわれます。 通常の360度を使って角度を表す体系はdegree体系と呼ばれています。 その間の変換は、次のようになります。なお、πを指定するときは、JavaではMath.PIと記述します。
radian角度 = degree角度 / 180 * π
例えば 90゜は1/2π
代表的な角度を以下に書き記してみました。
degree radian degree radian
0 → 0 180 → π
45 → π/ 4 270 → 3π/ 2
90 → π/ 2 360 → 2π
2つの角度体系を変換するために、Java2からは、以下の2つのメソッドが用意されました。計算結果は実数です。
double radian角度の変数 = Math.toRadians( degree角度 ) // radian角度に変換する
double degree角度の変数 = Math.toDegrees( radian角度 ) // degree角度に変換する
実際に、三角関数などを使った式を記述してみましょう。以下の記述では、まずは、角度の変換をしてから計算結果を求めています。
double theta = Math.toRadians( 60 ); // 60度をradian角度にする double result = Math.sin( theta ); // 60度のsinの値を求める
また次のように、引数の中に直に変換するメソッドを記述しても構いません。引数は内側から評価されます。
double result = Math.sin( Math.toRadians( 38 ) ); // sin 38 double ratio = Math.cos( Math.PI / 3 ); // cos 60 double theta = Math.toDegrees( Math.acos( 0.33 ) ); // cos-1 0.33 double alpha = Math.atan2( 0.0, -2.33 ); // alpha = pi
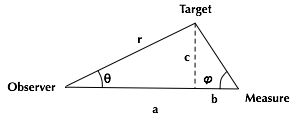
これは三角測量で使われていると思われます。まず、下図のようにTargetから、垂線を下ろします。これが底辺と交わった点から、 Measure(測定者)までの距離をbとします。また、垂線の長さをcとします。

このようにすると、bとcおよびa、rの関係から、rの大きさを次のようにθとφ、およびaから求めることができます。 以下はJavaのプログラムではなくて、単なる高等学校でやった関係式の変形です。
a = r * cos( θ ) + b … 底辺のaとbとの関係から、これを変形して b = a - r * cos( θ ) … (1) c = r * sin( θ ) … (2) 斜辺rと垂線cとの関係から tan( φ ) = c / b …(3) bと垂線cとの関係から tan( φ ) = (r * sin( θ )) / (a - r * cos(θ)) … (3)のcとbにそれぞれ(2)と(1)を代入 ( a - r * cos( θ ) ) * tan( φ ) = r * sin( θ ) … 右辺の分母を左辺に移動 a - r * cos( θ ) = ( r * sin( θ ) ) / tan( φ ) …左辺のtan( φ )を右辺に移動 a / r - cos( θ ) = sin( θ ) / tan( φ ) …両辺をrで割ってみた a / r = sin( θ ) / tan( φ ) + cos( θ ) …左辺にあったcos( θ )を右辺に移動 r / a = 1 / (sin( θ ) / tan( φ ) + cos( θ ) ) …両辺の分子分母を入れ替え r = a / (sin( θ ) / tan( φ ) + cos( θ ) ) …左辺のaを右辺に移動
指数は、二乗とか三乗とかのことですが、ここでは、指数としてマイナスや分数も入ったときにどう求めるかの公式を記しておきます。 以下でnとmとは、共に1以上の正の整数だと思ってください。
x0 = 1 どんな数でも0乗は1となります。
x-n = 1 / x n マイナスの指数は、逆数として扱われます
x1/n = n√x 1/n乗は、n乗根として扱われます。
xm/n = n√xm 上の法則の一般形
x-m/n = 1 / n√xm 上の法則のマイナスのときの一般形
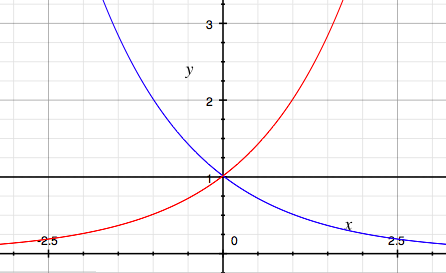
指数をグラフを観てみましょう。基数が1.0だと、指数は、何乗でもマイナス何乗でもとにかく、値は1.0のままです。 ところが、基数が0よりも大きく1.0未満だと、n乗のnの値を大きくするとだんだん小さくなっていきます。 逆に、基数が1.0よりも大きいと、n乗のnの値を大きくするとだんだん大きくなっていきます。 下記の図は、黒い線が「y = 1x」で、青い線が「y = 0.5x」で、赤い線が、「y = 2x」です。
指数の法則として次のような公式があります。aとbは、0より大きい正の数とします。
am × an = am+n
am ÷ an = am-n
( am )n = am×n
( a × b )n = an × bn
( a ÷ b )n = an ÷ bn
指数の結果とと基数から、指数を求めるのが対数です。下記の記述では、yの対数がxということになります。 このとき、基数aのことを「底」と呼ぶことがあります。 なお、底は0よりも大きい正の実数でなければなりません。
y = ax ⇔ x = log a y
対数の法則として次のような公式があります。 aとbは、0よりも大きくて、1でない正の数とします。また、MとNも0よりも大きい正の数とします。
log a a = 1
log a 1 = 0
log a ( M×N ) = log a M + log a N
log a ( M÷N ) = log a M - log a N
log a Mp = p × log a M
a loga M = M
log a M = log b M ÷ log b a
ここ3番目と4番目の2つの式に注目してください。 指数を使うと、「掛け算、割り算が、足し算、引き算に変換される」という性質があります。 これで、近代の科学技術計算の精度がぐっとあがりました。 何故かというと、数を対数に変換して、足し算・引き算をしてから、その結果を底の数のべき乗として計算すれば良くなったからです。 また、これを利用して「計算尺」なるものも作られました。 計算尺を使うことで、ある程度の精度(有効桁数4桁ぐらい)で、実数の掛け算・割り算が一瞬で計算できるようになりました。 また、最後の公式に注目してください。この公式があるおかげで、対数の底はなんでも良いことになります。 計算しやすい底を使って、対数を求めておいて、あとで、割り算すれば希望の底における指数を求めることができます。
そこで、対数の底として使われるのは、10と「ネイピア数」と呼ばれる自然対数の底が用いられます。 ネイピア数は、実はネイピアが求めたのではなく、後年にオイラーによって定義されたものです。 eという文字を使い始めたのもオイラーです。近代の戦争の時代に、オイラーは数学に大きな業績を残しました。 ほとんどオイラーが関与していない定理がないくらい、お馴染みの公式をびしばし作り出しています。 ところで自然対数の底は、次のような感じです。
e = 2.718281828459045235360287471352 …
底を10とする対数を「常用対数」と呼びますし、底をeを使う対数を「自然対数」と呼びます。 Javaでは、常用対数はlog10というメソッドで実現されていますし、自然対数はlogというメソッドで実現されています。 また、自然対数のべき乗はexpというメソッドが用意されています。 一般の指数については、powというメソッドが用意されています。
double ep = Math.exp( 3 ); // e3 double naturallog = Math.log( 1.34e5 ); // loge 1.34e5 double power = Math.pow( 10, 3 ); // 103 double commonlog = Math.log10( 1.34e5 ); // log10 1.34e5
入力してもらった2つの実数値について、その積と商を、そのまま求めてみるのと、対数を使って求めてみるのと両方でやってみましょう。 タートル・グラフィックスのライブラリのstartメソッドのところだけを記述しています。
public void start( ) {
double x = displayInputDialog( "Please input positive number: ", 27.35 );
double y = displayInputDialog( "Please input positive number other than zero: ", 3.1234 );
double result = x * y;
double logresult = Math.exp( Math.log( x ) + Math.log( y ) );
displayDialog( "Compare two result " + result + " with " + logresult );
result = x / y;
logresult = Math.exp( Math.log( x ) - Math.log( y ) );
displayDialog( "Compare two result " + result + " with " + logresult );
}
本編では、数値積分を台数公式を使って行ないましたが、他にも漸化式を使って、値を求める方法や、 極限に近づけていって値を求める方法、あるいはテイラー展開を使って近似値を求める方法があります。 あるいは統計の手法で値を求めたり、一様分布ではなくて、正規分布の乱数を使いたい場合もあります。 ここでは、それらの典型的な例を紹介しましょう。
古代バビロニアでは、√2を安定した方法で求めていました。 メソポタミア文明はすごいです。 まずは、x1を1.4としまして、次第に細かく求めていきます。 次の式で、xkは、k番目に求められた値だと思ってください。
xk+1 = xk / 2 + 1 / xk
これは、非常に速く収束して、√2に近づいて行きます。このように、1つ前の値から次の値を計算していく式を「漸化式」と呼びます。 プログラミングしてみましょう。
double x = 1.4;
int i=1;
while ( i <= 20 ) {
x = x / 2.0 + 1.0 / x;
System.out.println( "Square Root 2 is " + x );
i = i + 1;
}
すごいです。ここでは、20回の繰返しをしていますが、わずか、3回か4回の繰返しで、√2の値が正確に求まってしまいます。 最初のxを100としても、11回ぐらいの繰返しで求まります。なお、Excelを使ってもこのような漸化式を求めることができます。 どうして、この漸化式が古代バビロニアの人達はわかったのでしょうか。 なお、この漸化式は、近代に入りアイザック・ニュートンによって一般化され、「ニュートン法」とも呼ばれています。
自然対数の底eは次のような極限値として求まります。
e = lim ( 1 + 1 )n n→∞ n
ここでは、nを無限にするまで計算ができませんので、nの値を1から10倍ずつ大きくして1億までで求めてみましょう。 最後にMath.Eの値を表示します。
int n=1;
while ( n <= 100000000 ) {
double result = Math.pow( 1.0+1.0/n, n );
System.out.println( "e at n=" + n + " is " + result );
n = n * 10;
}
System.out.println( Math.E );
いろいろな関数は、テイラー展開(Taylor Series)と呼ばれる方法で計算することができます。以下は、Sine関数とCosine関数、および(1+x)のa乗に ついてテイラー展開された式を記述しています。なおn!は、nの階乗(n! = 1×2×…×n)です。また、xは、0に近い小さい値と思ってください。
sin(x) = x - 1 x3 + 1 x5 + … + 1 (-1)n-1 x2n-1 + … 3! 5! (2n-1)!
cos(x) = 1 - 1 x2 + 1 x4 + … + 1 (-1)n x2n + … 2! 4! (2n)!
(1 + x)a = 1 + ax + a(a-1) x2 + … + a(a-1)…(a-n+1) xn + … 2! n!
これを使って、0度から90度まで10度ずつ、第n項まで、足し算して(それを級数と呼びますが)値を求めてみましょう。 sine関数に付いて求めてみます。一緒にMath.sinの値の結果を表示しています。 内側の繰返しで、級数をnが大きい方から求めているのは、誤差を考慮してです。小さい数から足し合わせていきます。 アプリケーションで、mainメソッドと、階乗を求めるfactorialメソッドを記述しました。
public static void main(String [ ] args) {
int n = 10;
int angle =0;
while ( angle <= 90 ) {
double x = Math.toRadians( angle );
int i = n;
double result =0.0;
while ( i > 0 ) {
if ( (i - 1)%2 == 0 ) {
result = result +Math.pow( x, 2*i - 1) / factorial( 2*i -1 );
} else {
result = result - Math.pow( x, 2*i - 1) / factorial( 2*i -1 );
}
i = i - 1;
}
System.out.println( "Angle:" + angle + " result:" + result +
" Math.sin: " + Math.sin( Math.toRadians( angle ) ) );
angle = angle + 10;
}
}
static long factorial( int n ) {
if ( n == 1 ) { return 1; }
else { return (long)(n*factorial(n-1) ); }
}
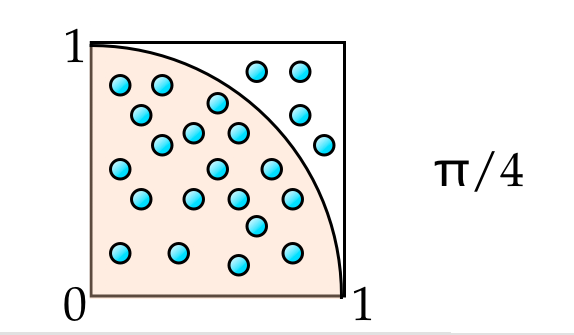
x2+y2 < r2全体で発生された個数の中で、正方形の面積 : 扇形の面積= 1: π/4ですから、この正方形のなかに、 n 個の点を落としたとき、count個の点が円内に落ちたとすれば以下の式からπが求められます。割り算は、 実数の割り算で行ないます。
1: π/4 = n : count ∴ π = 4 * count/n
Math.random( )やタートル・グラフィックスのライブラリで用意されているrandomInteger, random, randomNumberは、 一様分布の乱数を発生させます。これは、発生区間(たとえば、Math.random( )の場合は、0.0以上1.0未満)の間で、一様な確率で 乱数を発生させるものです。 そうではなくて、良く統計で使われる正規分布で乱数を発生させるような場合を考えてみます。 正規分布では、中央値の近くの値が一番良く発生し、中央から離れるに従って、値の発生率は低くなります。
Random 乱数用のオブジェクトのための変数 = new Random( 乱数系列の初期値 ); // これは最初のみ、初期値は長桁整数値
double 実数の変数 = 乱数変数.nextGaussian( ); // 乱数値を求めるとき(平均値0.0、分散1.0の正規分布の乱数)
なぜ初期値が必要なのかと言えば、疑似乱数なので、この初期値が同じだと、同じ乱数系列を発生させてしまいます。 ですから、毎回違う乱数の列が欲しければ、初期値を変える必要があります。 使用例は以下の通りです。
Random gauss = new Random( 10L ); // 乱数系列を初期化 double result = gauss.nextGaussian( ); // 1つ目の乱数を得る
なお、正規分布を発生させるRandomクラスは、java.utilパッケージに入っているので、プログラムの先頭に以下の一文が必要になります。
import java.util.*;
それでは、正規分布にしたがって、乱数を発生させてみましょう。 下記の記述では、現在時刻のミリ秒(getTimeInMillis())で最初の乱数系列の初期値を与えています。 ですから、実行するたびに、乱数系列が変わりますので、毎回の実行で同じ乱数系列が発生するということはありません。 1000回乱数を発生させています。分散(-1.0〜1.0)の区間内の乱数がどれくらい発生したか、変数countで数えて、 最後に表示しています。
Random gauss = new Random( (new GregorianCalendar( )).getTimeInMillis( ) );
int n = 1000;
int i = 1;
int count = 0;
while ( i <= n ) {
double number = gauss.nextGaussian( );
System.out.print( number + " " );
if ( i % 10 == 0 ) { System.out.println( ); }
if ( number >= -1.0 && number <= 1.0 ) { count++; }
i = i + 1;
}
System.out.println( count );
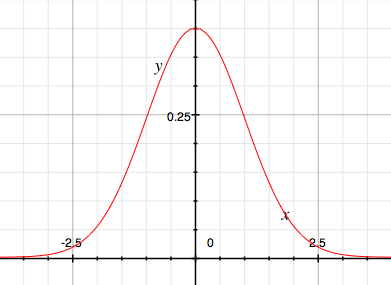
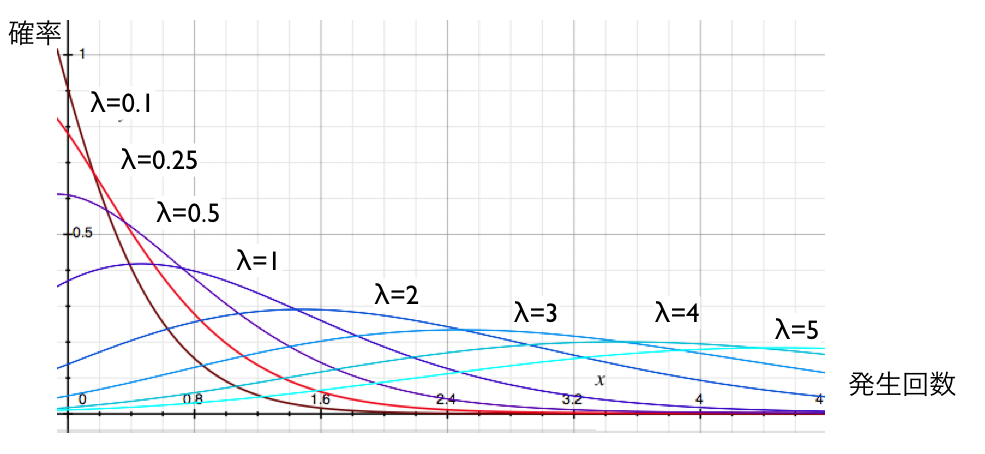
ポアソン分布は、確率分布と呼ばれるものです。 実世界のシミュレーションで事象が生起する確率を求めたいときによく使われます。 たとえば、お店でお客さんの到着率を求めるときなどに使われます。 以下のグラフは、単位時間中に平均λ回の確率で発生する事象が、丁度x回だけ発生する確率の分布を示しています。 なお、このλが充分に大きいと正規分布に近づいていくことが知られています。
| <<Developing Environments | ⋏ Return to Columns | >>Algorithms |