2. 構文と意味¶
2.1. 形式言語理論をちょっとだけ¶
2.1.1. 形式的な言語の定義¶
- アルファベット(alphabet)
言語を構成する文字の集合
- 文(sentence)
アルファベットを一列に並べたもの
- 文法(grammar)
文が正しいかどうかを決める規則
- 言語(language)
正しい文の集合
アルファベットから考えると話が長くなるので、適当なトークン(token)を最小単位とすることが多い。トークンは、文字を組み合わせた単語のようなものである。
トークンの例
total = total + x; はアルファベットの列としては、 t, o, t, a, l, 空白, =, 空白, t, o, ... だが、これでは面倒くさいので total, =, total, +, x, ; というトークン列として考える。
生成文法 とは、正しい文の集合を「次のようにして生成できる文全体の集合」と定義するやりかた。
終端記号(トークン)、非終端記号、生成規則
非終端記号の一つを開始記号に指定する
生成規則を適用することによって開始記号から文(終端記号の列)を作り出す。
簡単な文法
終端記号: I, you, love
非終端記号: S, N, V
開始記号: S
生成規則: S→NVN, N→I, N→you, V→love
生成文法をいくつかのクラス( チョムスキー階層 )に分類することができるが、ほとんどのプログラミング言語は文脈自由文法で表わすことができる。文脈自由文法とは、生成規則の適用対象がただ一つの非終端記号であるような文法。文脈(前後にどんな記号があるか)に関係なく生成規則を適用できる。
2.1.2. BNF 記法¶
BNF (Backus-Naur Form) は、文脈自由文法を書き表す便利な記法。いろいろな拡張バージョンもある。
終端記号は、そのまま書く。
非終端記号は、名前を < > で囲んで書く。
生成規則は、「非終端記号 ::= 右辺」という形。右辺は記号列を書き、複数の可能性がある場合は縦棒で区切って並べる。
変数、加算、乗算、括弧を含む式の文法
終端記号は A, B, C, +, *, (, )
非終端記号は <var>, <term>, <expr>
開始記号は <expr>
生成規則:
<var> ::= A | B | C
<term> ::= <var> | ( <expr> )
<expr> ::= <term> | <expr> + <term> | <expr> * <term>
2.1.3. 構文木¶
文がどのような生成規則によって生成されるか、見つけ出すことを構文解析(parse)と言う。構文木(parse tree)は、構文解析の結果を木構造で表わしたもの。
A*(B+C) の生成
<expr> → <expr>*<term> → <term>*<term> → <var>*<term> → A*<term> → A*(<expr>) → A*(<expr>+<term>) → A*(<term>+<term>) → A*(<var>+<term>) → A*(B+<term>) → A*(B+<var>) → A*(B+C)
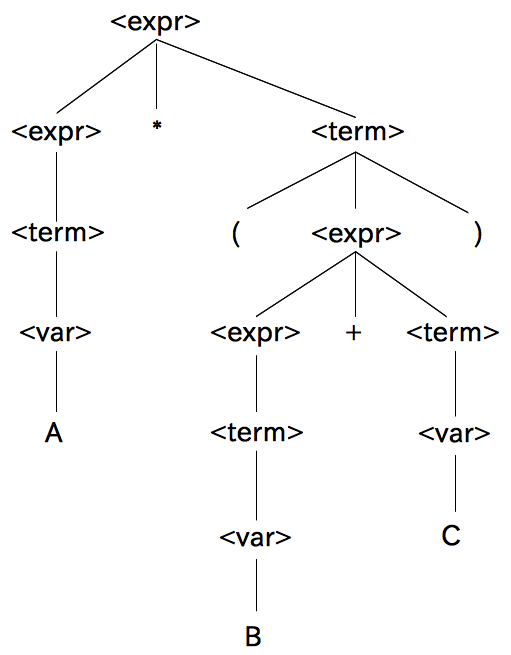
A*(B+C) の構文木¶
課題1
上の文法で A+B*C を構文解析し、構文木を描け。
【解答例】
課題2
上の文法では乗算と加算の間に優先順位がないが、乗算を加算より優先したい場合( A+B ではなく B*C が部分木になる)はどのような文法に変更すればよいか?ヒント:新しい非終端記号を追加し、加算の式と乗算の式を別のレベルにする。
【解答例】
2.1.4. 曖昧な文法¶
一つの文に対して、二種類以上の構文解析が可能な場合、その文法は曖昧である(ambiguous)と言う。
自然言語の場合
加算と乗算
次の文法に対して A*B+C は、二種類の異なる構文木が作れる。
<var> ::= A | B | C
<expr> ::= <var> | <expr> + <expr> | <expr> * <expr>
Dangling-else
CやJavaのif文はelseが省略可能なので、dangling else と呼ばれる問題が生じる。
<if-statement> ::= if ( <expr> ) <statement> |
if ( <expr> ) <statement> else <statement>
課題3
次のプログラムを例にして、dangling else を説明しなさい。
if ( x > 0) if ( y > 0 ) z = 1; else z = 2;
【解答例】
課題4
次の文法が曖昧であることを説明しなさい。
<a> ::= <a> <a> | A
【解答例】
2.2. 意味論をちらっと¶
意味を厳密に定義するのは、非常に難しい。例えば、C や Java で ++ 演算子は「式を評価した後、その変数の値を1増やす」と説明されることが多いが、これでは x = 1; x = x++; で何が起きるか、よくわからない。自然言語で定義する限り、曖昧さはなくせないので、形式的な手法が必要になる。
意味論はパラダイムによって大きく違う。関数型言語はλ計算、論理型言語は一階述語論理を基礎としているので、それによって意味を定めることができる。命令形言語にはそのような理論的基礎が無いので、どのようにして形式的意味論は定めるか、次のようにしていろいろと研究されてきた。
2.2.1. 操作的意味論¶
発想としては、実際より簡単な機械や言語を想定して、その動作によって実行を説明する。すると今度はその簡単な機械や言語の意味はどうやって決めるかという話になってきりがない。厳密にするためには、計算ステップのモデル化と、それに関する論理体系を使用する必要がある。
計算ステップとは、コンピュータの状態が変化すること。
コンピュータの状態とは、例えば変数から値への写像(メモリの内容をモデル化したもの)。
論理的な推論規則によって、どのような計算ステップが可能かを指定する。
2.2.2. 公理的意味論¶
文の実行前に成り立つ論理式と、実行後に成り立つ論理式の関係( ホーア論理 )によって、文の意味を定める。
プログラムの正当性の証明と深い関係がある。プログラムが「正しい」とは、仕様の通りに動くということである。公理的意味論における仕様は、実行開始前に成り立っている論理式と、実行終了後に成り立つべき論理式によって定める。プログラムを構成している文それぞれに関するホーア論理の式を用いて、プログラム全体が正しいことを証明する。
2.2.3. 表示的意味論¶
再帰的関数や領域理論を基礎とし、プログラムの構成要素全てに、数学的な構造(数、集合、関数など)を対応させる。
プログラムの実行に伴う状態の変化を記述する点は操作的意味論と同じだが、それを推論体系でなく数学的構造で表現するところが違う。無限ループなども理論的にきれいに取り扱うことができるが、ものすごく難解な数式になってしまうところが欠点。