図8-7 円と三角関数
Home >> Columns >> Graphics and Curves
▼原点の移動次に、ウィンドウのサイズが決まっていますので、そのサイズに合わせて、直線や曲線を拡大・縮小させなければなりません。この拡大・縮小率をx座標方向をa、y座標方向をbとしますと、最終的に以下の式が得られます。
wx = x + dx
wy = -y + dy
▼原点の移動、および拡大・縮小率を考慮なお、ウィンドウのサイズ(幅と高さ)が整数値と求められます。getWidth( )メソッドとgetHeight( )メソッドです。 上記のdxやdyのための数値として、その半分の値を使うことができるでしょう。そうすると、原点はウィンドウの中心になります。
wx = a * x + dx
wy = - b * y + dy
int centerX = getWidth( ) / 2; int centerY = getHeight( ) / 2;
パラメータ形式で表わされる曲線のことを、パラメトリック曲線(Parametric Curve)と呼びますが、この曲線を、以上のような形でn本の折れ線で近似するためには、つぎのプログラムの断片で描くことになります。以下の描画方法で、x = f( t )やy=g( t )とは、tを使った何らかの式(あるいは関数)で、xやyが描かれるということを示しています。
- 陽関数形式
- 一方の座標を元にもう一方の座標を計算します。例:y = x2
- 陰関数形式
- 2つの座標値の関係性だけが表されます。例:x2+y2+r2=0
- パラメータ形式
- 媒介変数tを元に、x座標やy座標を計算します。tの動く範囲は、0〜1あるいは、0〜2π(角度の場合)になります。 例:x = cos( t ), y = sin( t )
▼パラメトリック曲線の描画方法
double delta = 1.0 / n; // tを0〜1の間で移動させるときのステップ間隔
double t = 0.0;
turtle.upPen( );
turtle.setLocation( f( 0 ), g( 0 ) );
turtle.downPen( );
for ( int i=1; i <= n; i++ ) {
t += delta;
double x = f( t ), y = g( t );
turtle.moveTo( x, y );
}
f( t ) = t * 200 - 100 + centerX // xの変化範囲が0を中心とする-100から100の範囲とする g( t ) = - ( t*200 -100) * (t*200-100) * 0.015 + centerY // 0.015は縮小率実際のプログラムのプログラムとして、記述してみましょう。たとえば、折れ線の数であるnを100とします。型変換も含めると次のように記述できます。startメソッドの部分だけを記述しました。
public void start( ) {
Turtle turtle = new Turtle( this );
int centerX = getWidth( ) / 2;
int centerY = getHeight( ) / 2;
int n = 100;
double delta = 1.0 / n;
double t = 0.0;
turtle.upPen( );
turtle.setLocation( -100 + centerX, -100*-100*0.015+centerY );
turtle.downPen( );
for ( int i=1; i <= n; i++ ) {
t += delta;
double x = ( t * 200) - 100 + centerX;
double y = -(t*200-100) *(t*200-100) *0.015+ 150;
turtle.moveTo( x, y );
}
}
実行結果を以下に示します。この実行結果では、x座標、y座標を青色で、放物線を赤色で表示するようにしました。
図8-6 放物線を表わしたプログラム
x = r * cos( t )
y = r * sin( t )

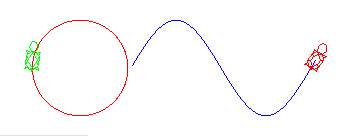
図8-7 円と三角関数
int degree = 35; double theta = Math.toRadians( degree );なお上記のコメントのように、この変換をするための関数として、Math.toRadiansと、Math.toDegreesがJava2から用意されているのは、既にご紹介しました。ここまでわかれば、あとはxおよびy座標を、radian角度と三角関数で求めることはできます。いま、半径80ドットぐらいを目安に考えましょう。しかしながら、プログラムのx座標y座標は、0からしか始まっていませんし、しかもy座標は逆になっています。そこで、中心をウィンドウ上の中心座標に置くように考えて、ウィンドウ上のx座標、y座標は次のような形で求めることになります。
double radius = 80; x = Math.cos( theta ) * radius + centerX; y = -Math.sin( theta ) * radius + centerY;パラメトリック曲線を描く手法で描いていきます。ただし、今回は、パラメータ変数の変化範囲は、0から2πになります。最初は、上の式にtheta=0を代入しますと(radius+centerX, centerY)になりますので、最初はそこから始めましょう。という訳で、繰返しを使って角度は、0度から360度まで動かしてみて、線を描くようなプログラムを作ってみましょう。やはり、startメソッドの部分だけ記述します。
public void start( ) {
turtle.setPenColor( Red );
turtle.upPen( );
turtle.setLocation( centerX, 0 );
turtle.downPen( );
turtle.back( centerY*2 );// y軸
turtle.upPen( );
turtle.setLocation( 0, centerY );
turtle.downPen( );
turtle.right( centerX*2 );// x軸
turtle.setPenColor( Blue );
turtle.upPen( );
turtle.setLocation( centerX+radius, centerY );
turtle.downPen( );
for (int i=1; i<=360; i++ ) {
double theta = Math.toRadians( i );
double x = Math.cos( theta ) * radius + centerX;
double y = -Math.sin( theta ) * radius + centerY;
turtle.moveTo( x, y );
}
}
}
B( t ) = ( 1 - t )3P0 + 3t( 1 - t )2P1 + 3t2( 1 -t )P2 + t3P3この式は、バーンスタイン関数と呼ばれています。それぞれのPiには、各制御点のx座標またはy座標が入ります。x座標とも、y座標とも同じ形の式で計算できるのです。これを使って、配列に格納されている4つの座標値を用いて、ベジェ曲線を描画するようなアプレットを作ってみました。paintメソッドの部分だけを示しています。1-tをいちいち記述するのは面倒なので、ct(Complement for t の意)という名前の変数に入れています。第7章で説明した、折れ線で近似する方式で描きますが、曲線上の各頂点の座標を配列に求めています。そして、ガイドとなる折れ線も、近似したベジェ曲線もdrawPolylineを使って描いています。
public void paint (Graphics g) {
int px[ ] = { 30, 70, 130, 200 }; // 制御点のx座標の配列
int py[ ] = { 170, 50, 20, 165 }; // 制御点のy座標の配列
g.setColor( Color.blue );
g.drawPolyline( px, py, px.length ); // ガイドの折れ線
int n = 100; // 100本の直線で近似
double t, ct, delta;
int bx[ ] = new int[ n+1 ];
int by[ ] = new int[ n+1 ];
delta = 1.0/n;
t = 0.0;
for ( int i=0; i <= n; i++ ) {
ct = 1 - t;
bx[ i ] = (int)( ct*ct*ct*px[ 0 ] + 3*t*ct*ct*px[ 1 ]+ 3*t*t*ct*px[ 2 ] + t*t*t*px[ 3 ] );
by[ i ] = (int)( ct*ct*ct*py[ 0 ] + 3*t*ct*ct*py[ 1 ]+ 3*t*t*ct*py[ 2 ] + t*t*t*py[ 3 ] );
t = t + delta;
}
g.setColor( Color.red );
g.drawPolyline( bx, by, bx.length );
}
螺旋は、円と似ているのですが、円の半径が角度が変化していくについて変化していきます。この変化について、一定の割合で変化していくものと、指数的に変化していくものがあり、ここではその2つについて簡単に描画してみることにしましょう。
タートル・グラフィックスでは、単に、forwardとrotateだけを使って螺旋を描くことが可能です。 rotateは一定の角度で回ります。しかし、繰返しの中で毎回動く距離を徐々に大きく変えていきます。実数計算を使えば可能です。 これは、蚊取り線香のような形になり、代数螺旋(アルキメデスの螺旋)と呼ばれています。
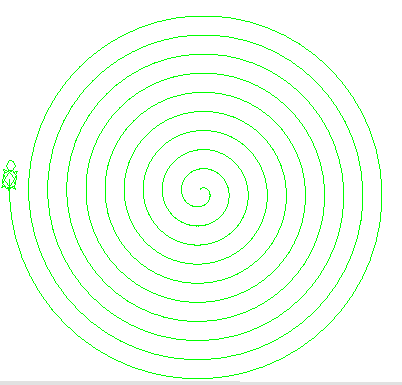
forwardとrotateだけを使って螺旋を描くタートルを動かして見なさい。クラス名はDrawSpiralで。
回転角度も変えるようにします。毎回rotateで回る角度が、補数や逆数を作ってだんだん小さくなるようにします。 さらに、繰返しの中で毎回進む距離を徐々に大きく変えていきます。実数計算を使えば可能です。 これは、巻貝のような形になり、対数螺旋と呼ばれています。
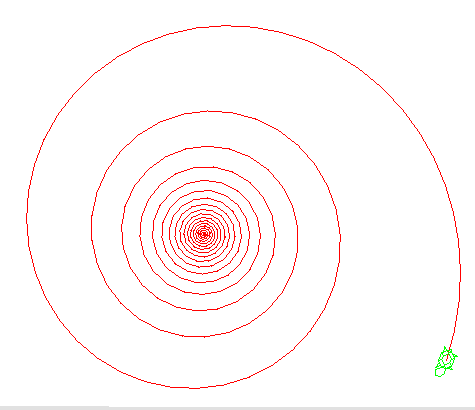
forwardとrotateだけを使って螺旋を描くタートルを動かして見なさい。クラス名はDrawLogarithmSpiralで。
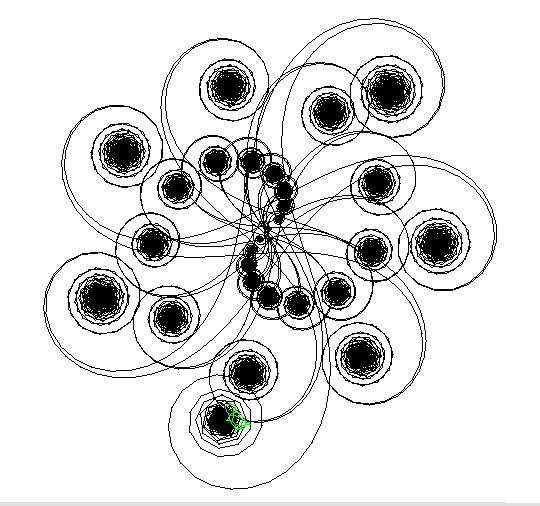
次のようなプログラムを入力したら、以下のような複雑な螺旋図形が描けました。どうしてだか わかりません。MicroWorldsのページには、 うまく螺旋が並んだ図形が描けています。どのような値を入れるとこうなるのかわかりません。 もし、MicroWorldsのページにあるような下の方の図形が描けた人には、アイスクリームをプレゼント致します。 また、この仕組みが解説できた人(履修学生に限る)には、教科書を謹呈致します。 またもや、startメソッドの中だけを記述しています。 クラス名は、Practice0704ですが、下の方の図形描画に果敢に挑戦するときは、クラス名はWiredSprialで作成してみてください。 実行は、「NoWait」でしないと何分も待つことになります。
Turtle turtle = new Turtle( this );
double increment = displayInputNumberDialog( "0.80から2.10まで", 0.999992 ); // この数値が怪しい!
printLine( increment );
double turn = 0.0;
double step = 0;
while ( turn <= 9999 ) {
turtle.forward( step );
turtle.rotate( turn );
turn = turn + increment;
step = step +0.002;
}

螺旋は、円と似ているのですが、円の半径が角度が変化していくについて変化していきます。この変化について、一定の割合で変化していくものと、指数的に変化していくものがあり、ここではその2つについて簡単に描画してみることにしましょう。
まずは、単に、forwardとrotateだけを使って螺旋を描くことが可能です。これは、以下に述べる代数螺旋になります。 rotateは一定の角度で回ります。しかし、繰返しの中で毎回動く範囲を徐々に変えていきます。実数計算を使えば可能です。
x = c *θ * cos( θ ), y = c * θ * sin( θ )この螺旋をプログラムで描画してみましょう。半径を100としまして、360度で半径の大きさになるようにcの値を設定します。startメソッドの部分だけを記述してあります。cを求めるのに、一番大きな角度である360×回転数で半径で割っておき、それに角度を掛けるようにしてあります。
public void start( ) {
Turtle turtle = new Turtle( this );
int centerX = getWidth( ) / 2;
int centerY = getHeight( ) / 2;
double radius = 80;
turtle.upPen( );
turtle.setLocation( centerX, centerY );
turtle.downPen( );
double c = radius / (360.0 * 8); // 8 は回転数
for (int i=0; i<=360 * 8; i++ ) {
double theta = Math.toRadians( i );
double x = Math.cos( theta ) * c * i + centerX;
double y = - Math.sin( theta ) * c * i + centerY;
turtle.moveTo( x, y );
}
}
x = acθ cos θ, y = acθ sin θこのプログラムでは、10回転ぐらいさせてみましょう。上の式から考えると、a = e(自然対数)とおきますと対数を使って、c = log( r )/ θとなります。startメソッドだけ記述しますと、以下のようになります。なお、θは、ラジアン体系を使っています。
public void start( ) {
Turtle turtle = new Turtle( this );
int centerX = getWidth( ) / 2;
int centerY = getHeight( ) / 2;
double radius = 80;
turtle.upPen( );
turtle.setLocation( centerX, centerY );
turtle.downPen( );
double c = Math.log( radius ) / ( 10 * 2 * Math.PI);
for (int i=0; i<=360 * 10; i++ ) {
double theta = Math.toRadians( i );
double x = Math.cos( theta ) * Math.pow( Math.E, c * theta) + centerX;
double y = - Math.sin( theta ) * Math.pow( Math.E, c * theta ) + centerY;
turtle.moveTo( x, y );
}
}
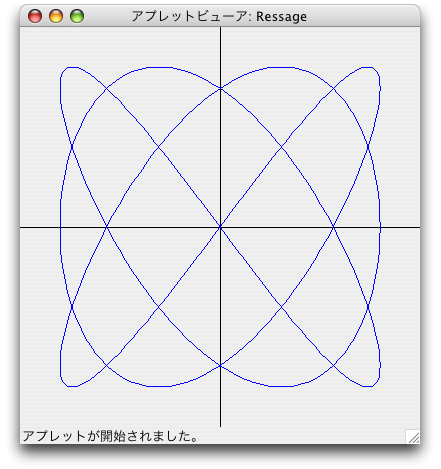
図8-8 リサージュ図形
x = (int) (Math.cos( theta*2 ) * radius + centerX); // 2倍2倍!たとえば、上のようにx座標を求める式で、cos関数の角度を2倍するだけで、変な図形が出てきます。これをリサージュ図形と言うらしいのです。これ繰返しを使って何倍にもできるようにしちゃえ!って感じで次のプログラムを作ってみました。インスタンス変数zoomに倍率をいれておき、どんどん倍率が+1されていくのが特徴です。4倍まで変わります。倍率が変わるたびに、色を変えるようにしました。該当部分だけ記述しました。
for ( int zoom =1; zoom <= 4; zoom ++ ) {
turtle.setPenColor( (zoom == 1 ) ? Blue : ( zoom == 2 ) ? Red :
( zoom == 3 ) ? Orange : Green );
turtle.upPen( );
turtle.setLocation( centerX+radius, centerY );
turtle.downPen( );
for (int i=1; i<=360; i++ ) {
double theta = Math.toRadians( i );
double x = Math.cos( theta ) * radius *zoom + centerX;
double y = -Math.sin( theta ) * radius + centerY;
turtle.moveTo( x, y );
}
}
Turtle turtle;
public void start( ) {
Color colors [ ] = { Red, Orange, Magenta, Blue };
turtle = new Turtle( this );
for ( int i=20; i <=80; i += 20 ) {
turtle.setPenColor( colors[ i/20-1 ] );
drawEpicycloid( 50+i, i, i / 5, 360*i/20, i*14, getHeight()/2 );
}
}
void drawEpicycloid( int rc, int rm, int rot, int n, int centerx, int centery ) {
double delta = Math.PI * 2 * rot / n;
double t = 0.0;
turtle.penup( );
turtle.setLocation( rc-2*rm+centerx, centery );
turtle.pendown( );
for ( int i=1; i <= n; i++ ) {
t += delta;
double x = (rc-rm)*Math.cos( t ) - rm*Math.cos( (double)(rc+rm)/rm * t ) + centerx;
double y = (rc-rm)*Math.sin( t ) - rm*Math.sin( (double)(rc+rm)/rm * t ) + centery;
turtle.moveTo( x, y );
}
}
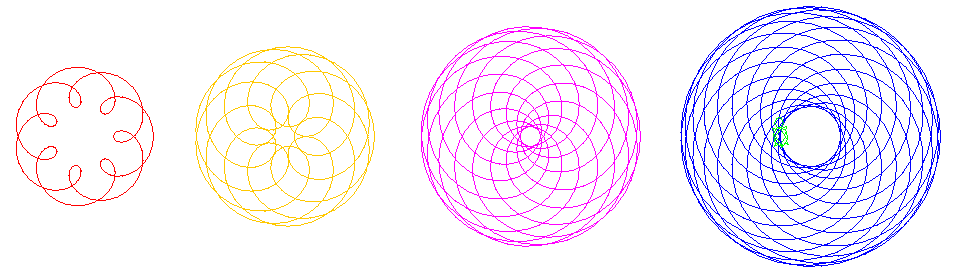
外サイクロイド
| <<Java Array and Strings | ⋏ Return to Columns | >>Calendars |