地震の規模と頻度の法則から、大地震の発生可能性について考える(1)
東北地方太平洋沖地震によって亡くなられた方々のご冥福をお祈りいたします。そして、現在も被災地において、あるいは避難先において、不自由な生活を余儀なくされている方々に、心よりお見舞い申し上げます。
2011年3月11日に発生した東北地方太平洋沖地震では、大地震の被害のみならず、そこから派生した大津波や原発の問題などによって、大きな被害・不安が続いている。このような状況のなかで、僕はなかなか仕事が手につかなかったのだが、少しずつ動き始めたいと思う。そこでまずは、研究者としての専門を活かしながら、地震について見つめ直すことから始めたい。
ここでは、地震の規模と頻度の法則と、近年の日本の実データから、大地震の発生可能性について考えることにしたい。
地震の規模と頻度に関しては、「グーテンベルク・リヒター則」(Gutenberg-Richter Law)という法則が知られている。この法則によれば、地震の規模 M と発生頻度(あるいは発生数) N の関係は、次の式で表される。
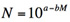
ここで、a と b は定数であり、地域によって異なる値をとる(なお、厳密に言うと、「頻度」はその規模の地震の発生回数を全事象数で割ることで求めるのだが、ここでは直感的なわかりやすさのために、「頻度(回数)」としてまとめて表記することにする)。
この式をグラフにすると、次のような感じになる。横軸が規模、縦軸が頻度(回数)なので、規模が大きくなるほど、発生する頻度(回数)は、ぐっと小さくなっていく、ということがわかる。
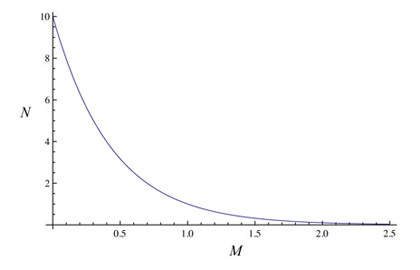
図1:グーテンベルク・リヒター則の式のかたち[線形グラフ](a=1, b=1)
まったく同じものを、別のグラフ表現で表すと、この法則がもつ特徴がより明確に示される。次のグラフは、縦軸の頻度(回数)の軸を対数軸(log)にしたものである。対数軸なので、縦軸は1目盛り進むごとに10倍になっている。このような軸の取り方でプロットすると、グーテンベルク・リヒター則の式は、直線のかたちになる。
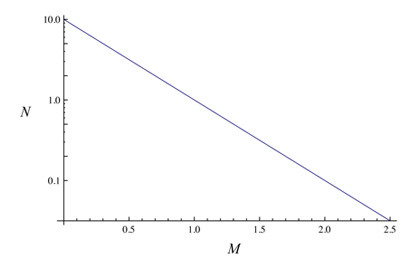
図2:グーテンベルク・リヒター則の式のかたち[対数グラフ](a=1, b=1)
複雑系科学やネットワーク科学の知識がある人ならば、どこかで見覚えのあるグラフだろう。そう、この地震の規模と頻度は、まさに「べき乗則」(power law)に従っているのである。地震の規模を表すマグニチュードは、地震のエネルギーの対数で計算されるので、グラフの横軸にエネルギーEをとれば、横軸も対数軸となる。このように、グーテンベルク・リヒター則は、べき乗則を示す現象の古典的な例として知られている。
さて、グーテンベルク・リヒター則を直感的に理解するために、具体的な数字を用いて説明をすることにしよう。
地震の規模と頻度の関係は、マグニチュードが 1 小さいと発生頻度が約10倍になる―――大雑把にいうと、こういうことだ。例えば、日本では、マグニチュード7クラスの地震が年に1回くらいの頻度で発生しているので、マグニチュード6クラスの地震は年に約10回、マグニチュード5クラスの地震は年に100回、マグニチュード4クラスの地震は年に1000回という計算になる。
逆に言えば、マグニチュードが1大きい地震は約10分の1の頻度で起きるということも意味している。例えば、マグニチュード8クラスの地震は年に約0.1回の頻度で発生する、つまり10年に1回くらい起きるという計算になる。さらに、マグニチュード9クラスの地震は年に約0.01回、つまり100年に1回という計算になる(もちろん、ここで言っているのは確率の話なので、100年に必ずぴったり1回しか起きないということではない。100年に2回来ることもあるし、来ないこともある。あくまでも確率的な傾向の話である点に注意)。
ここで注目に値するのは、マグニチュードが大きくなっても、(理論上は)確率は完全に0にはならないという点である。つまり、かなり大きな地震はごく稀にしか起きないが、起きないことはない、ということである。わずかでも起こる可能性はある。大地震は忘れたころにやってくる、と言われるが、まさに、この「起きにくさ」が防災の意識や対策・準備を怠りがちな理由であろう。かなり大きな地震も、ごく稀にだが起きる ――― この点は、決して忘れてはならない。
(つづく)
※公開当初は、独自のデータ分析の結果も掲載していましたが、データに不備があったため、続きは、後日再度アップします。すみません。
Refenreces
●『複雑系入門:知のフロンティアへの冒険』(井庭 崇, 福原 義久, NTT出版, 1998)
以前この本で、グーテンベルク・リヒター則とべき乗則の簡単な説明をした。
●『歴史は「べき乗則」で動く:種の絶滅から戦争までを読み解く複雑系科学』(マーク・ブキャナン, ハヤカワ文庫NF, 早川書房, 2009)[Mark Buchanan, Ubiquity: Why Catastrophes Happen, 200/2002]
地震の事例も含め、べき乗則をめぐる研究者たちの探究を紹介している。べき乗則になる地震モデルについての紹介もある。
●『地震予知の最新科学』(佃 為成, サイエンスアイ新書, ソフトバンククリエイティブ, 2007)
地震が発生する仕組みや、規模と頻度の関係などについての解説がある。
2011年3月11日に発生した東北地方太平洋沖地震では、大地震の被害のみならず、そこから派生した大津波や原発の問題などによって、大きな被害・不安が続いている。このような状況のなかで、僕はなかなか仕事が手につかなかったのだが、少しずつ動き始めたいと思う。そこでまずは、研究者としての専門を活かしながら、地震について見つめ直すことから始めたい。
ここでは、地震の規模と頻度の法則と、近年の日本の実データから、大地震の発生可能性について考えることにしたい。
地震の規模と頻度に関しては、「グーテンベルク・リヒター則」(Gutenberg-Richter Law)という法則が知られている。この法則によれば、地震の規模 M と発生頻度(あるいは発生数) N の関係は、次の式で表される。
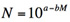
ここで、a と b は定数であり、地域によって異なる値をとる(なお、厳密に言うと、「頻度」はその規模の地震の発生回数を全事象数で割ることで求めるのだが、ここでは直感的なわかりやすさのために、「頻度(回数)」としてまとめて表記することにする)。
この式をグラフにすると、次のような感じになる。横軸が規模、縦軸が頻度(回数)なので、規模が大きくなるほど、発生する頻度(回数)は、ぐっと小さくなっていく、ということがわかる。

図1:グーテンベルク・リヒター則の式のかたち[線形グラフ](a=1, b=1)
まったく同じものを、別のグラフ表現で表すと、この法則がもつ特徴がより明確に示される。次のグラフは、縦軸の頻度(回数)の軸を対数軸(log)にしたものである。対数軸なので、縦軸は1目盛り進むごとに10倍になっている。このような軸の取り方でプロットすると、グーテンベルク・リヒター則の式は、直線のかたちになる。

図2:グーテンベルク・リヒター則の式のかたち[対数グラフ](a=1, b=1)
複雑系科学やネットワーク科学の知識がある人ならば、どこかで見覚えのあるグラフだろう。そう、この地震の規模と頻度は、まさに「べき乗則」(power law)に従っているのである。地震の規模を表すマグニチュードは、地震のエネルギーの対数で計算されるので、グラフの横軸にエネルギーEをとれば、横軸も対数軸となる。このように、グーテンベルク・リヒター則は、べき乗則を示す現象の古典的な例として知られている。
さて、グーテンベルク・リヒター則を直感的に理解するために、具体的な数字を用いて説明をすることにしよう。
地震の規模と頻度の関係は、マグニチュードが 1 小さいと発生頻度が約10倍になる―――大雑把にいうと、こういうことだ。例えば、日本では、マグニチュード7クラスの地震が年に1回くらいの頻度で発生しているので、マグニチュード6クラスの地震は年に約10回、マグニチュード5クラスの地震は年に100回、マグニチュード4クラスの地震は年に1000回という計算になる。
逆に言えば、マグニチュードが1大きい地震は約10分の1の頻度で起きるということも意味している。例えば、マグニチュード8クラスの地震は年に約0.1回の頻度で発生する、つまり10年に1回くらい起きるという計算になる。さらに、マグニチュード9クラスの地震は年に約0.01回、つまり100年に1回という計算になる(もちろん、ここで言っているのは確率の話なので、100年に必ずぴったり1回しか起きないということではない。100年に2回来ることもあるし、来ないこともある。あくまでも確率的な傾向の話である点に注意)。
ここで注目に値するのは、マグニチュードが大きくなっても、(理論上は)確率は完全に0にはならないという点である。つまり、かなり大きな地震はごく稀にしか起きないが、起きないことはない、ということである。わずかでも起こる可能性はある。大地震は忘れたころにやってくる、と言われるが、まさに、この「起きにくさ」が防災の意識や対策・準備を怠りがちな理由であろう。かなり大きな地震も、ごく稀にだが起きる ――― この点は、決して忘れてはならない。
(つづく)
※公開当初は、独自のデータ分析の結果も掲載していましたが、データに不備があったため、続きは、後日再度アップします。すみません。
Refenreces
●『複雑系入門:知のフロンティアへの冒険』(井庭 崇, 福原 義久, NTT出版, 1998)
以前この本で、グーテンベルク・リヒター則とべき乗則の簡単な説明をした。
●『歴史は「べき乗則」で動く:種の絶滅から戦争までを読み解く複雑系科学』(マーク・ブキャナン, ハヤカワ文庫NF, 早川書房, 2009)[Mark Buchanan, Ubiquity: Why Catastrophes Happen, 200/2002]
地震の事例も含め、べき乗則をめぐる研究者たちの探究を紹介している。べき乗則になる地震モデルについての紹介もある。
●『地震予知の最新科学』(佃 為成, サイエンスアイ新書, ソフトバンククリエイティブ, 2007)
地震が発生する仕組みや、規模と頻度の関係などについての解説がある。
複雑系科学 | - | -