井庭崇のConcept Walk

今週のインターリアリティプロジェクトの輪読では、『歴史の方程式』の前半を読んだ。

この本は、「べき乗分布」に関する研究の歴史を振り返り、「非平衡物理学」(nonequilibrium physics)―――著者の言葉でいうと「歴史物理学」(historical physics)―――の考え方を紹介してくれる、とても刺激的で重要な本だ。ここまで「べき乗分布」の研究について詳しく書いてくれている本は他にはない。

今日は、この本のなかから僕が特に面白いと思う部分を紹介することにしたい。

■べき乗分布にはスケール不変性がある → 「典型的」「一般的」な出来事はない。

凍ったジャガイモを壁や床に叩きつけると砕け散るが、そのとき様々なサイズの破片ができる。粉々になった小さな破片は非常に多く、大きな塊は少ないだろう。ここで、この破片の大きさと数を詳しく調べてみると、実は規則正しいということがわかってくる。「重ささが二倍になるごとに、破片の数は約六分の一になっていく」(p.59)というのだ。これは、数学的にいうならば、「べき乗分布」になっているということだ。

「べき乗分布」には、スケール不変的(scale-invariant)な性質がある。つまり、どのスケール（尺度）で拡大してみても、同じような状況が見えるのである。このことをわかりやすくいうと、次のようになる。

「今あなたが、好きなように自分の体の大きさを変えられる存在だったとしよう。・・・どんな大きさでもまわりの景色はまったく同じに見えるので、もし自分を何回縮めたか忘れてしまうと、まわりを見ただけでは自分の大きさがまったく分からなくなってしまうのである。これが、冪乗則の意味するところである。破片の山は必ず、「スケール不変性」や自己相似性と呼ばれる特別な性質をもっているからである。破片が広がった様子はどの大きさにおいても同じに見え、まるで各部分が全体の縮小像であるかのように見えるということだ。」(p.61)

つまり、どのスケールで見ても、同じような秩序が見うけられるということだ。バラバシたちが、リンク数の順位分布がべき乗分布になるネットワークを「スケールフリー・ネットワーク」と呼んだのは、このためだ。

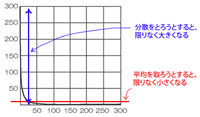べき乗分布においては、「典型的な」もしくは「一般的な」サイズというものは存在しない。あらゆるスケールのものが同じようなかたちで存在するからである。正規分布では重要な指標であった「平均」や「分散」というものが意味をなさなくなる。というのは、平均をとると、テールに引っ張られて平均値は限りなく小さくなってしまう。また、分散を調べると、ヘッドの値とテールの値にかなりの差があるため、かぎりなく大きな分散値になってしまう。このように、平均や分散という指標は、正規分布でなければ意味をなさないのだ。そのため、対象の分布が正規分布なのかべき乗分布なのかということはとても重要なことになる。

さらに、サンプリングの考え方も、正規分布を前提とする場合とは話が違ってくる。正規分布であれば、サンプリング数を増やすことで、より精度の高い近似ができるが、べき乗分布の場合は、サンプリング数を増やすほど、テール部分を拾ってしまい、値は小さくなってしまう。ここでも、対象となる現象が正規分布なのかべき乗分布なのかは、重要な違いだといえる。


■べき乗分布にはスケール不変性がある → 大きな出来事に特別な理由はない。

べき乗分布のスケール不変性は、大きな出来事が何か特別な理由によるものではない、ということも意味している。それは、大きな出来事も小さな出来事も、同じメカニズムで生成されるからだ。

「ジャガイモの破片の山におけるスケール不変性は、大きい破片は小さい破片を拡大したものにすぎないということを示している。すべての大きさの破片は、あらゆる大きさで同じように働く崩壊過程の結果として生じる。グーテンベルク＝リヒターの法則は、地震や、地震を発生させる地殻で起こる過程についても、同様のことが言えるということを示している。地震のエネルギーは冪乗則に従うので、その分布はスケール不変的になる。大きな地震が小さな地震とは違う原因で起こると示唆するものは、まったく何もないのである。大きな地震が特別なものである理由がないという事実は、小さな地震を引き起こすものと大きな地震を引き起こすものはまったく同じであるという、逆説的な結果を示唆している。この考え方にもとづけば、大地震に対する特別な説明を探しても意味がないことになる。」(p.63)

このことを印象的に示すために、コロンビア大学の地震の専門家クリストファー・ショルツの言葉が紹介されている。「地震は、起こりはじめたときには、自分がどれほど大きくなっていくか知らない。」(p.98)。大地震というのは、地震の連鎖の雪崩によって結果として大地震になったのであり、その背後にあるメカニズムは、小規模の地震や中規模の地震と同じメカニズムによるということだ。


以上のことを、僕らの商品市場の研究成果と絡めて考えてみることにしたい。すでに紹介したように（「書籍販売市場における隠れた法則性」）、井庭研では、書籍販売市場などの実データ解析をしているが、そこでもべき乗分布が発見されている。このことは何を意味するのだろうか。

まず最初に、書籍販売市場において「典型的な」あるいは「一般的な」商品というものは存在しないということである。平均と分散で商品を見ることはできない、ということである。これはおそらく現場レベルではずいぶんまえからわかっていたことだと思う。販売冊数-順位のべき乗分布は、それが統計的にも言えるということを示している。

さらに、販売冊数-順位のべき乗分布は、大ヒットをした商品が売れた理由は、何か特別な理由があるからではない、ということ示唆している。このことは、大地震がスケールに依存しない普遍的なメカニズムによって、地震の連鎖の雪崩によって結果として生まれたというのと同じように、商品の大ヒットも市場の普遍的なメカニズムによって、「売れるものがますます売れる」という連鎖の雪崩によって、結果として生まれるのかもしれない。そうすると、僕らはマーケティングや市場戦略というものをどう考えればよいのだろうか………とても興味深い。（この点については、また別の機会に議論することにしたい。）

このように、べき乗分布について考えるときには、商品市場の例がわかりやすく、想像力豊かに考えることができる。そう思って、僕はべき乗分布のインプリケーションについて考えるときはいつも、市場のべき乗分布で考えている。なかなかおすすめの方法だ。